Hoe u een tweerichtings-anova uitvoert in excel
Een tweewegs-ANOVA (“variantieanalyse”) wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen die over twee factoren zijn verdeeld.
In deze zelfstudie wordt uitgelegd hoe u een tweerichtings-ANOVA uitvoert in Excel.
Voorbeeld: Tweerichtings-ANOVA in Excel
Een botanicus wil weten of de plantengroei wordt beïnvloed door blootstelling aan zonlicht en de frequentie van water geven. Ze plant 40 zaden en laat ze twee maanden lang groeien onder verschillende omstandigheden wat betreft blootstelling aan de zon en waterfrequentie. Na twee maanden registreert ze de hoogte van elke plant. De resultaten worden hieronder weergegeven:

In de bovenstaande tabel zien we dat er onder elke combinatie van omstandigheden vijf planten werden gekweekt. Er werden bijvoorbeeld vijf planten gekweekt met dagelijks water en zonder zonlicht en hun hoogten na twee maanden waren 4,8 inch, 4,4 inch, 3,2 inch, 3,9 inch en 4,4 inch:

We kunnen de volgende stappen gebruiken om een tweerichtings-ANOVA op deze gegevens uit te voeren:
Stap 1: Selecteer de Data Analysis Toolpak.
Klik op het tabblad Gegevens op Gegevensanalyse :

Als u dit niet als optie ziet, moet u eerst de gratis Data Analysis Toolpak laden .
2. Kies Anova: twee factoren met replicatie
Selecteer de optie met de tekst Anova: Two-Factor With Replication en klik vervolgens op OK .
In deze context verwijst ‘replicatie’ naar het hebben van meerdere observaties in elke groep. Veel planten werden bijvoorbeeld gekweekt zonder blootstelling aan zonlicht en zonder dagelijkse watergift. Als we in plaats daarvan slechts één plant zouden kweken in elke combinatie van omstandigheden, zouden we „geen replicatie“ gebruiken, maar onze steekproefomvang zou veel kleiner zijn.
3. Vul de benodigde waarden in.
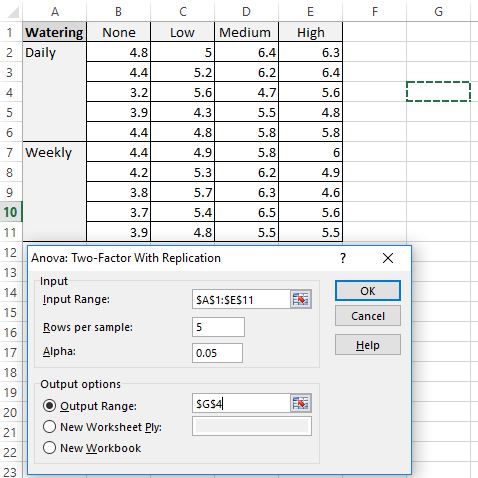
Vul vervolgens de volgende waarden in:
- Invoerbereik: Selecteer het cellenbereik waarin onze gegevens zich bevinden, inclusief headers.
- Rijen per monster: Typ “5” omdat er in elk monster 5 planten zitten.
- Alfa: Kies een significantieniveau dat u wilt gebruiken. Wij kiezen 0,05.
- Uitvoerbereik: Kies een cel waarin u de tweeweg-ANOVA-uitvoer wilt laten verschijnen. We kiezen cel $G$4.
Stap 4: Interpreteer het resultaat.
Zodra we op OK klikken, verschijnt het tweerichtings-ANOVA-resultaat:
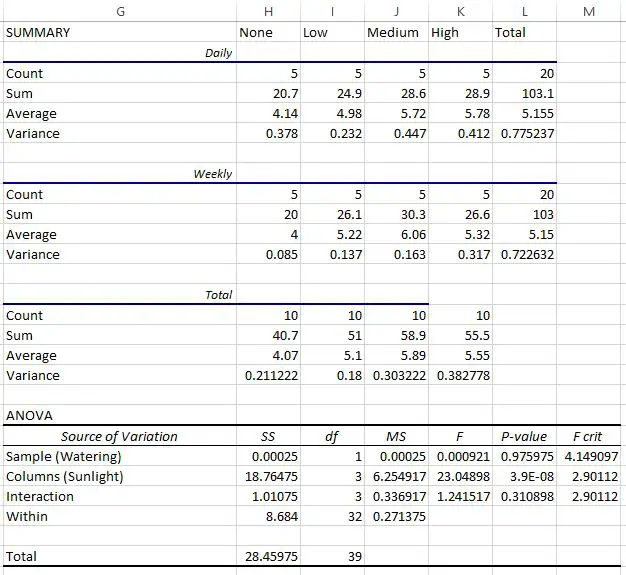
De eerste drie tabellen geven samenvattende statistieken voor elke groep weer. Bijvoorbeeld:
- De gemiddelde hoogte van planten die dagelijks water kregen, maar zonder zonlicht, was 10,10 meter.
- De gemiddelde hoogte van planten die wekelijks water kregen en weinig zonlicht kregen, was 15,22 centimeter.
- De gemiddelde hoogte van alle planten die dagelijks water kregen, was 5,115 inch.
- De gemiddelde hoogte van alle planten die elke week water kregen, was 15,5 cm.
- De gemiddelde hoogte van alle planten bij blootstelling aan zware zon was 5,55 inch.
Enzovoort.
De laatste tabel toont het resultaat van de tweeweg-ANOVA. We kunnen het volgende waarnemen:
- De p-waarde voor de interactie tussen de waterfrequentie en de blootstelling aan de zon was 0,310898 . Dit is niet statistisch significant op het alfaniveau van 0,05.
- De p-waarde voor de bewateringsfrequentie was 0,975975 . Dit is niet statistisch significant op het alfaniveau van 0,05.
- De p-waarde voor blootstelling aan de zon was 3,9E-8 (0,000000039) . Dit is statistisch significant op het alfaniveau van 0,05.
Deze resultaten geven aan dat blootstelling aan de zon de enige factor is met een statistisch significant effect op de planthoogte. En omdat er geen interactie-effect is, is het effect van blootstelling aan de zon consistent op elk niveau van de bewateringsfrequentie. Simpel gezegd: of een plant dagelijks of wekelijks water krijgt, heeft geen invloed op de invloed van blootstelling aan de zon op een plant.