Handmatig een anova met herhaalde metingen uitvoeren
Een ANOVA met herhaalde metingen wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer groepen waarin dezelfde onderwerpen in elke groep voorkomen.
In deze zelfstudie wordt uitgelegd hoe u handmatig een ANOVA met herhaalde metingen in één richting uitvoert.
Voorbeeld: herhaalde ANOVA-metingen in één richting met de hand
Onderzoekers willen weten of drie verschillende medicijnen verschillende reactietijden veroorzaken. Om dit te testen meten ze de reactietijd (in seconden) van vijf patiënten op elk medicijn. De resultaten worden hieronder weergegeven:
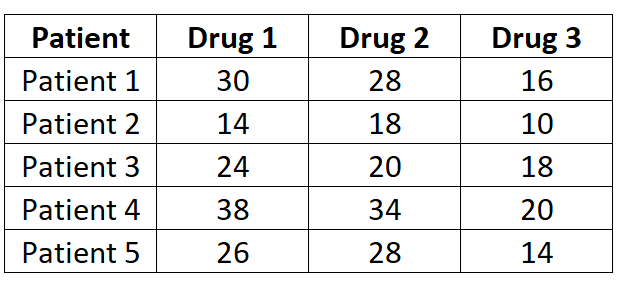
Omdat bij elke patiënt elk van de drie medicijnen wordt gemeten, gebruiken we een ANOVA met herhaalde metingen in één richting om te bepalen of de gemiddelde reactietijd tussen medicijnen verschilt.
Volg de volgende stappen om ANOVA met herhaalde metingen handmatig uit te voeren:
Stap 1: Bereken de SST.
Eerst berekenen we de totale som van kwadraten (SST), die kan worden gevonden met behulp van de volgende formule:
SST = s 2 totaal (n totaal -1)
Goud:
- s 2 totaal : de variantie voor de dataset
- n totaal : het totale aantal waarnemingen in de dataset
In dit voorbeeld berekenen we de SST als volgt: (64,2667)(15-1) = 899,7
Stap 2: Bereken SSB
Vervolgens berekenen we de som van de kwadraten (SSB), die kan worden gevonden met behulp van de volgende formule:
SSB = Σn j ( X j – x totaal ) 2
Goud:
- Σ : een Grieks symbool dat “som” betekent
- n j : het totale aantal waarnemingen in de j- de groep
- x j : het gemiddelde van de jde groep
- x totaal : het gemiddelde van alle gegevens
In dit voorbeeld berekenen we SSB als volgt: (5)(26,4-22,533) 2 +(5)(25,6-22,533) 2 + (5)(15,6-22,533) 2 = 362,1
Stap 3: Bereken de SSS.
Vervolgens berekenen we de subject sum of squares (SSS), die kan worden gevonden met behulp van de volgende formule:
SSS =(Σr 2 k /c) – (N 2 /rc)
Goud:
- Σ : een Grieks symbool dat “som” betekent
- r 2 k : kwadratische som van de k- de patiënt
- N: het eindtotaal van alle gegevens
- r: totaal aantal patiënten
- c: totaal aantal groepen
In dit voorbeeld berekenen we SSS als volgt: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441,1
Stap 4: Bereken SES.
Vervolgens berekenen we de som van de kwadratische fout (SSE), die kan worden gevonden met behulp van de volgende formule:
SSE = SST – SSB – SSS
In dit voorbeeld berekenen we de SES als volgt: 899,7 – 362,1 – 441,1 = 96,5
Stap 5: Vul de ANOVA-tabel met herhaalde metingen in.
Nu we SSB, SSS en SSE hebben, kunnen we de ANOVA-tabel met herhaalde metingen invullen:
| Bron | Som van kwadraten (SS) | df | Gemiddelde kwadraten (MS) | F |
|---|---|---|---|---|
| Tussen | 362,1 | 2 | 181,1 | 15.006 |
| Onderwerp | 441,1 | 4 | 110,3 | |
| Fout | 96,5 | 8 | 12.1 |
Zo hebben we de verschillende getallen in de tabel berekend:
- df tussen: #groepen – 1 = 3 – 1 = 2
- df onderwerp: #deelnemers – 1 = 5 – 1 = 4
- Fout df: df tussen * df onderwerp = 2*4 = 8
- MS komt binnen: SSB / df komt binnen = 362,1 / 2 = 181,1
- MS-onderwerp: SSS-onderwerp / df = 441,1 / 4 = 110,3
- MS-fout: SSE-fout / df = 96,5 / 8 = 12,1
- F: MS komt binnen / MS-fout = 181,1 / 12,1 = 15,006
Stap 6: Interpreteer de resultaten.
De F-teststatistiek voor deze ANOVA met herhaalde metingen in één richting is 15,006 . Om te bepalen of dit een statistisch significant resultaat is, moeten we het vergelijken met de kritische F-waarde in de F-verdelingstabel met de volgende waarden:
- α (significantieniveau) = 0,05
- DF1 (vrijheidsgraden van de teller) = df tussen = 2
- DF2 (vrijheidsgraden van de noemer) = fout df = 8
We vinden dat de kritische waarde van F 4,459 is.
Omdat de F-teststatistiek in de ANOVA-tabel groter is dan de kritische waarde F in de F-verdelingstabel, verwerpen we de nulhypothese. Dit betekent dat we voldoende bewijs hebben om te zeggen dat er een statistisch significant verschil bestaat tussen de gemiddelde responstijden van de medicijnen.