Hoe u een mann-whitney u-test uitvoert in spss

Een Mann-Whitney U-test (ook wel een Wilcoxon-rangsomtest genoemd) wordt gebruikt om de verschillen tussen twee steekproeven te vergelijken wanneer de steekproefverdeling niet normaal verdeeld is en de steekproefomvang klein is (n <30). Het wordt beschouwd als het niet-parametrische equivalent van de t-test met twee steekproeven .

In deze tutorial wordt uitgelegd hoe u een Mann-Whitney U-test uitvoert in SPSS.

Voorbeeld: Mann-Whitney U-test in SPSS

Onderzoekers willen weten of brandstofbehandeling een verandering in het gemiddelde mpg van een auto veroorzaakt. Om dit te testen voeren ze een experiment uit waarbij ze het mpg meten van 12 auto’s met brandstofbehandeling en 12 auto’s zonder behandeling.

De volgende schermafbeelding toont het mpg van elke auto samen met de groep waartoe deze behoort (0 = geen brandstofbehandeling, 1 = brandstofbehandeling):

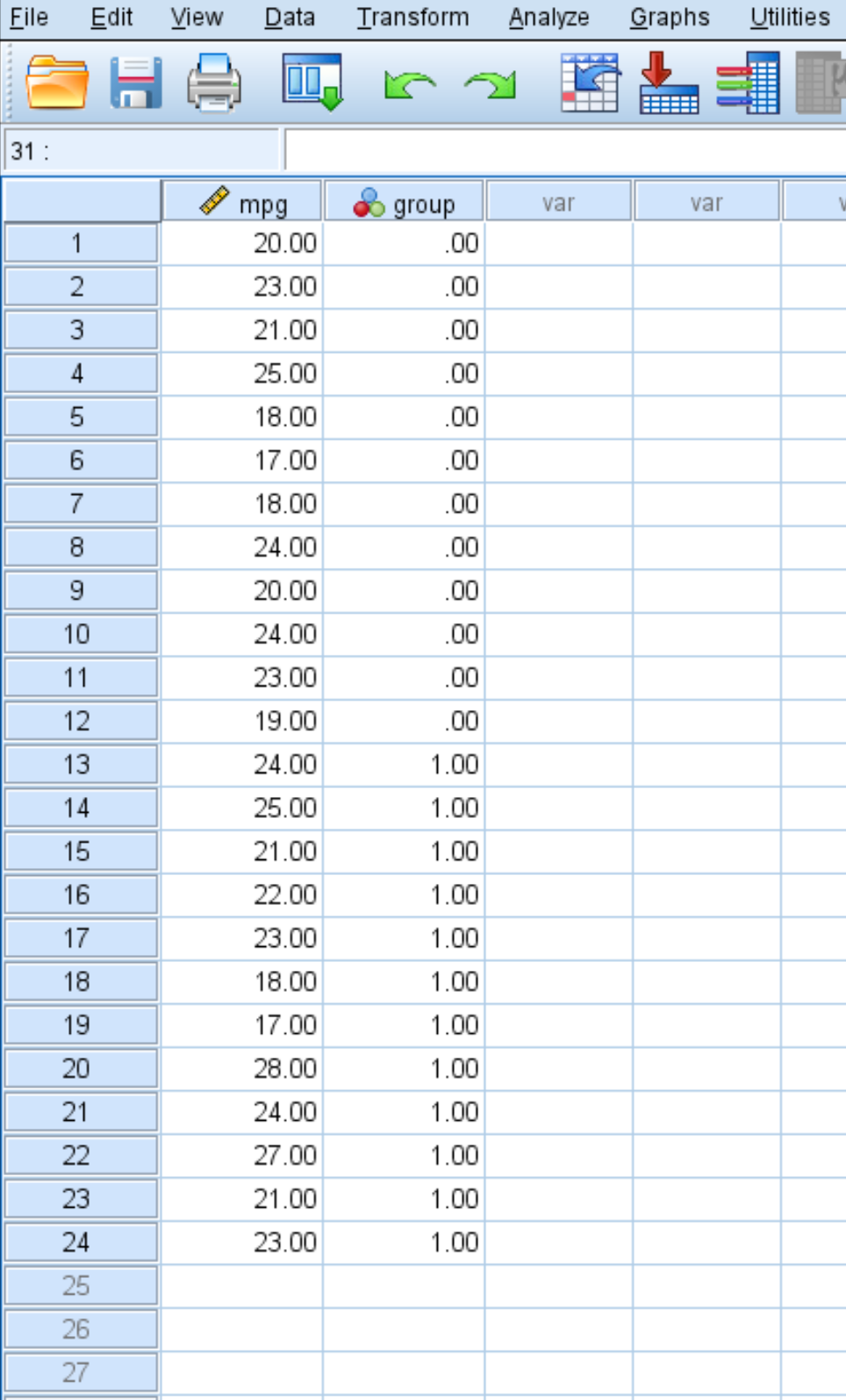
Omdat de steekproefomvang klein is en de onderzoekers vermoeden dat de steekproefverdeling niet normaal verdeeld is, besloten ze een Mann-Whitney U-test uit te voeren om te bepalen of er een statistisch significant verschil in mpg tussen de twee groepen bestaat.

Voer de volgende stappen uit om een Mann-Whitney U-test uit te voeren in SPSS.

Stap 1: Selecteer de Mann-Whitney U-testoptie.

Klik op het tabblad Analyseren , vervolgens op Niet-parametrische tests , vervolgens op Legacy Dialogs en vervolgens op 2 onafhankelijke voorbeelden :

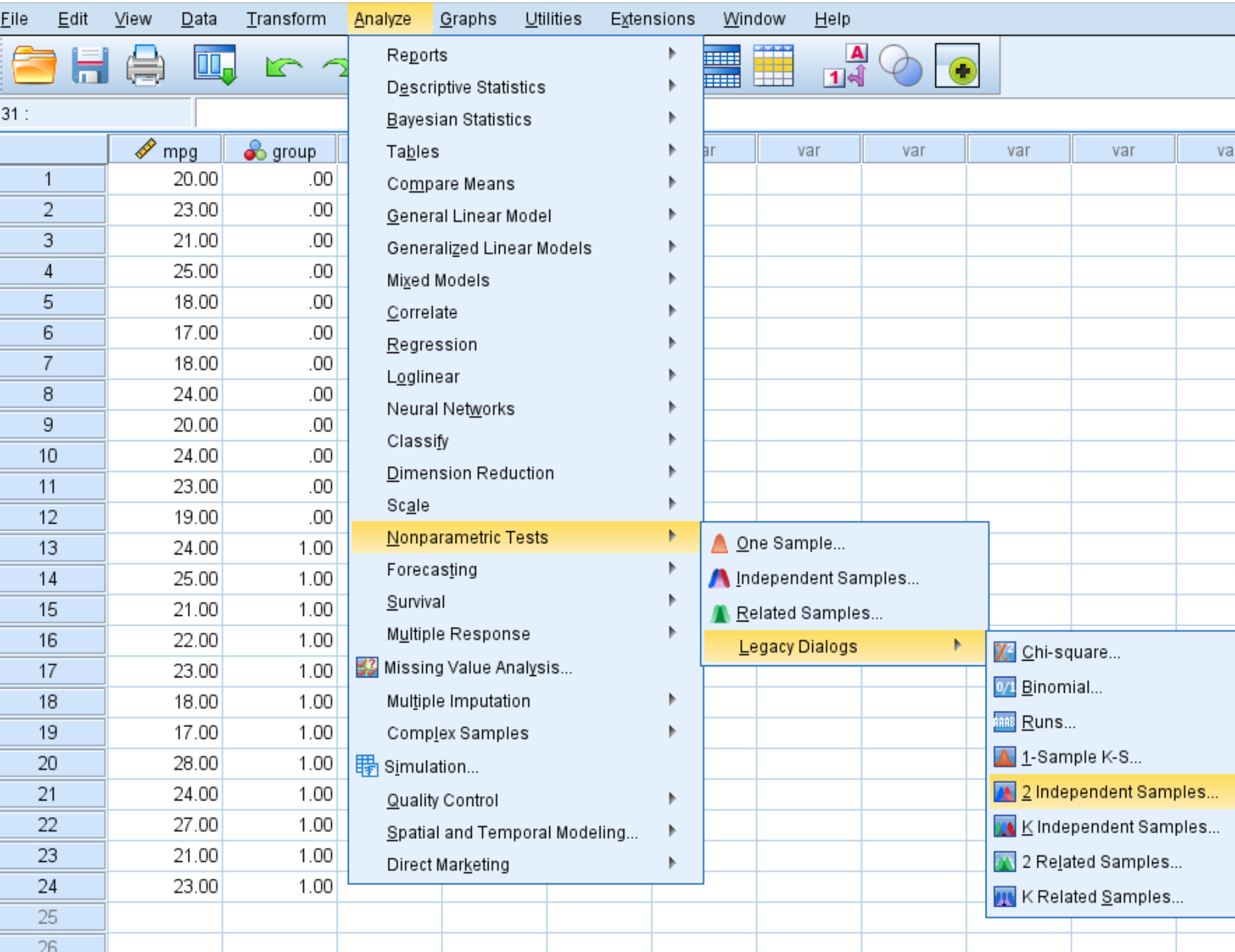
Stap 2: Vul de benodigde waarden in om de test uit te voeren.

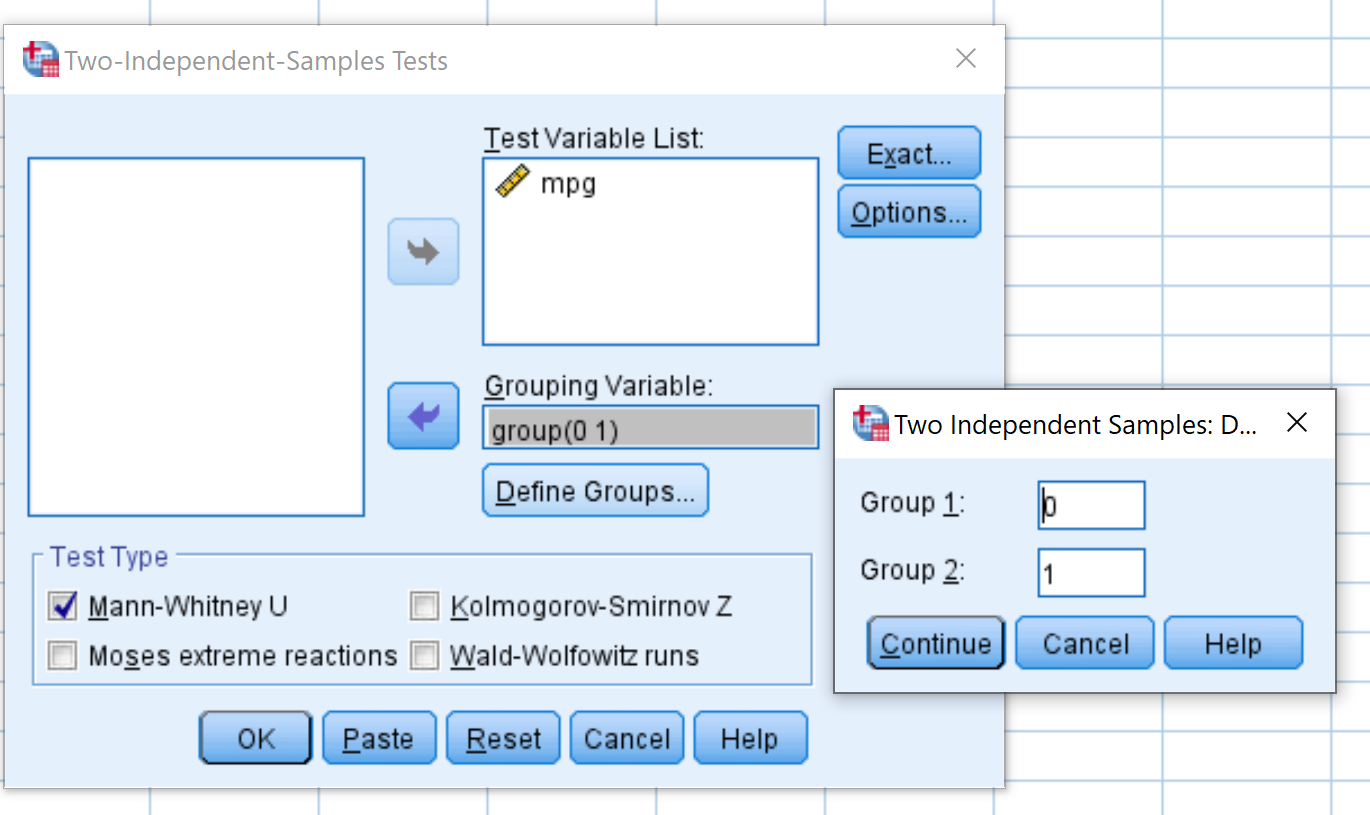
Sleep mpg naar het gebied met de naam Testvariabelenlijst en groepeer het in het gebied met de naam Groeperingsvariabele . Klik op Groepen definiëren en definieer groep 1 als rijen met waarde 0 en definieer groep 2 als rijen met waarde 1.

Zorg ervoor dat het vakje naast Mann-Whitney U is aangevinkt. Klik vervolgens op OK .

Stap 3: Interpreteer de resultaten.

Zodra u op OK klikt, worden de Mann-Whitney U-testresultaten weergegeven:

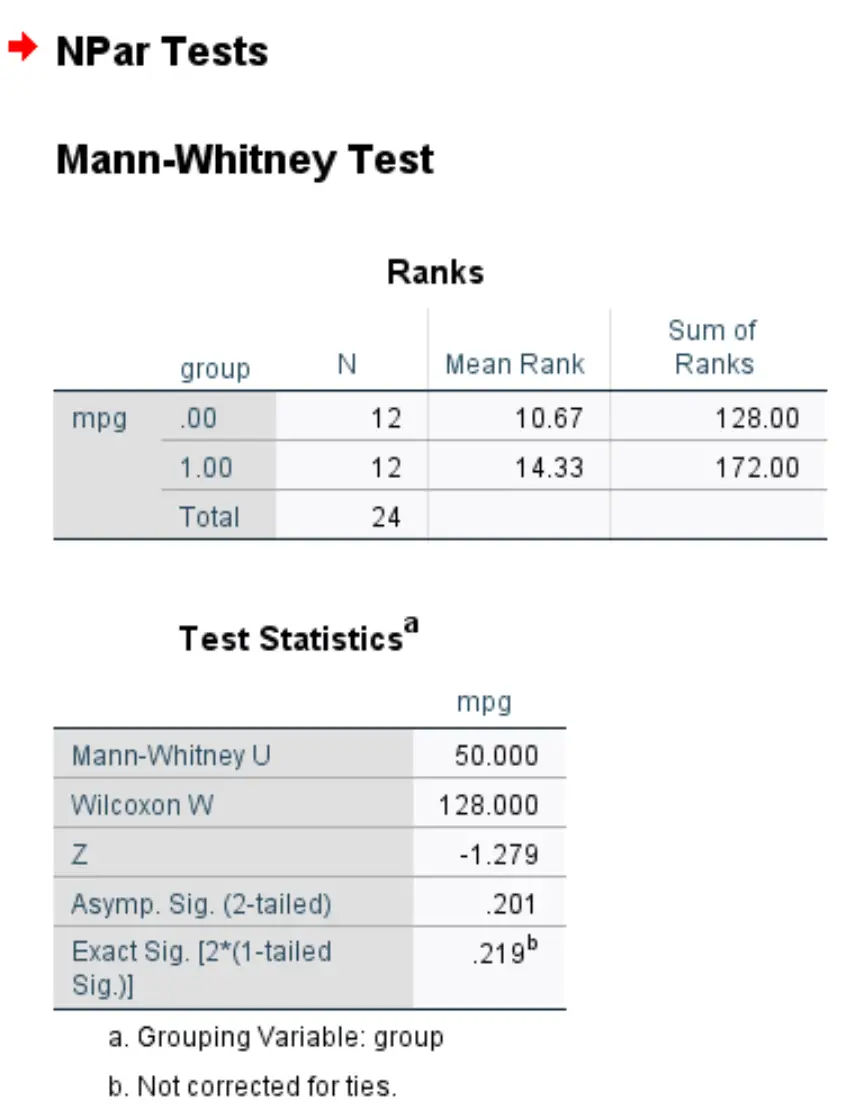
De belangrijkste getallen in het resultaat zijn de Z-teststatistiek en de tweezijdige asymptotische p-waarde:

• Z-teststatistiek: -1,279
• p-waarde: 0,201

Omdat de p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen. We hebben niet genoeg bewijs om te zeggen dat het werkelijke gemiddelde mpg tussen de twee groepen verschillend is.

Stap 4: Rapporteer de resultaten.

Ten slotte zullen we de resultaten van onze Mann-Whitney U-test rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een Mann-Whitney U-test uitgevoerd op 24 auto’s om te bepalen of een nieuwe brandstofbehandeling een verschil in het gemiddelde aantal kilometers per gallon veroorzaakte. Elke groep had 12 auto’s.

De resultaten toonden aan dat de gemiddelde mpg niet statistisch verschillend was tussen de twee groepen (z = -1,279, p = 0,2010) op een significantieniveau van 0,05.

Op basis van deze resultaten heeft de nieuwe brandstofbehandeling geen significante invloed op het aantal kilometers per gallon van auto’s.