Relatieve standaardafwijking
In dit artikel wordt uitgelegd hoe u de relatieve standaardafwijking kunt berekenen. U zult ontdekken wat de relatieve standaarddeviatie is, wat de formule ervan is, evenals een oefening die stap voor stap wordt opgelost.
Wat is relatieve standaarddeviatie?
Relatieve standaarddeviatie is een statistische maatstaf die de spreiding van een dataset ten opzichte van het gemiddelde aangeeft. De relatieve standaardafwijking wordt berekend door de standaardafwijking van de gegevens te delen door het gemiddelde.
De relatieve standaardafwijking wordt uitgedrukt als een percentage en de waarde ervan zal altijd positief zijn.
De interpretatie van de relatieve standaarddeviatie wordt gebruikt om de spreiding van een gegevensmonster weer te geven. Hoe groter de waarde van de relatieve standaarddeviatie, hoe meer verspreid de gegevens. En hoe kleiner de relatieve standaarddeviatie, hoe dichter de gegevens bij het gemiddelde liggen.
Over het algemeen wordt het acroniem RSD gebruikt als symbool voor relatieve standaardafwijking .
Relatieve standaardafwijkingsformule
De relatieve standaardafwijking is gelijk aan de standaardafwijking gedeeld door het gemiddelde vermenigvuldigd met 100. Om de relatieve standaardafwijking te berekenen, moet u daarom eerst de standaardafwijking en het rekenkundig gemiddelde bepalen, vervolgens de twee statistische metingen delen en ten slotte vermenigvuldigen met 100.
Met andere woorden, de formule voor de relatieve standaardafwijking is:
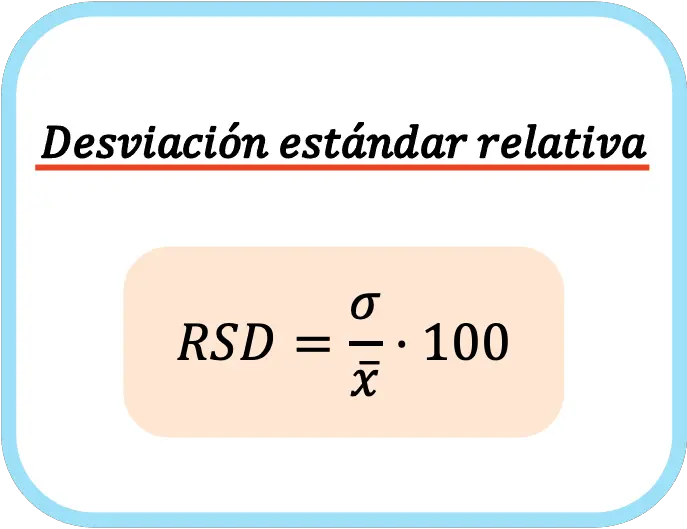
Bij het berekenen van de relatieve standaardafwijking wordt deze met honderd vermenigvuldigd om de waarde als percentage uit te drukken.
Voorbeeld van het berekenen van de relatieve standaardafwijking
Nadat u de definitie van relatieve standaarddeviatie en de formule ervan heeft bekeken, ziet u hieronder een concreet voorbeeld van hoe de relatieve standaarddeviatie wordt berekend.
- Bereken de relatieve standaardafwijking van de volgende statistische gegevensset:
4, 1, 3, 9, 12, 2, 5, 8, 3, 6
Eerst moeten we de standaardafwijking van de gegevens vinden:
![]()
Ten tweede berekenen we het rekenkundig gemiddelde van de gegevens:
![]()
Zodra we de standaardafwijking en het rekenkundig gemiddelde van de gegevensreeksen kennen, gebruiken we de formule voor de relatieve standaardafwijking.
![]()
En ten slotte vervangen we de berekende waarden in de formule en berekenen we de relatieve standaardafwijking:
![]()