Hoe logistische regressie uit te voeren in spss

Logistische regressie is een methode die we gebruiken om een regressiemodel te fitten wanneer de responsvariabele binair is.

In deze tutorial wordt uitgelegd hoe u logistische regressie uitvoert in SPSS.

Voorbeeld: logistische regressie in SPSS

Gebruik de volgende stappen om logistische regressie uit te voeren in SPSS voor een dataset die aangeeft of universiteitsbasketbalspelers wel of niet zijn opgeroepen voor de NBA (concept: 0 = nee, 1 = ja) op basis van hun GPA. punten per spel en hun divisieniveau.

Stap 1: Voer de gegevens in.

Voer eerst de volgende gegevens in:

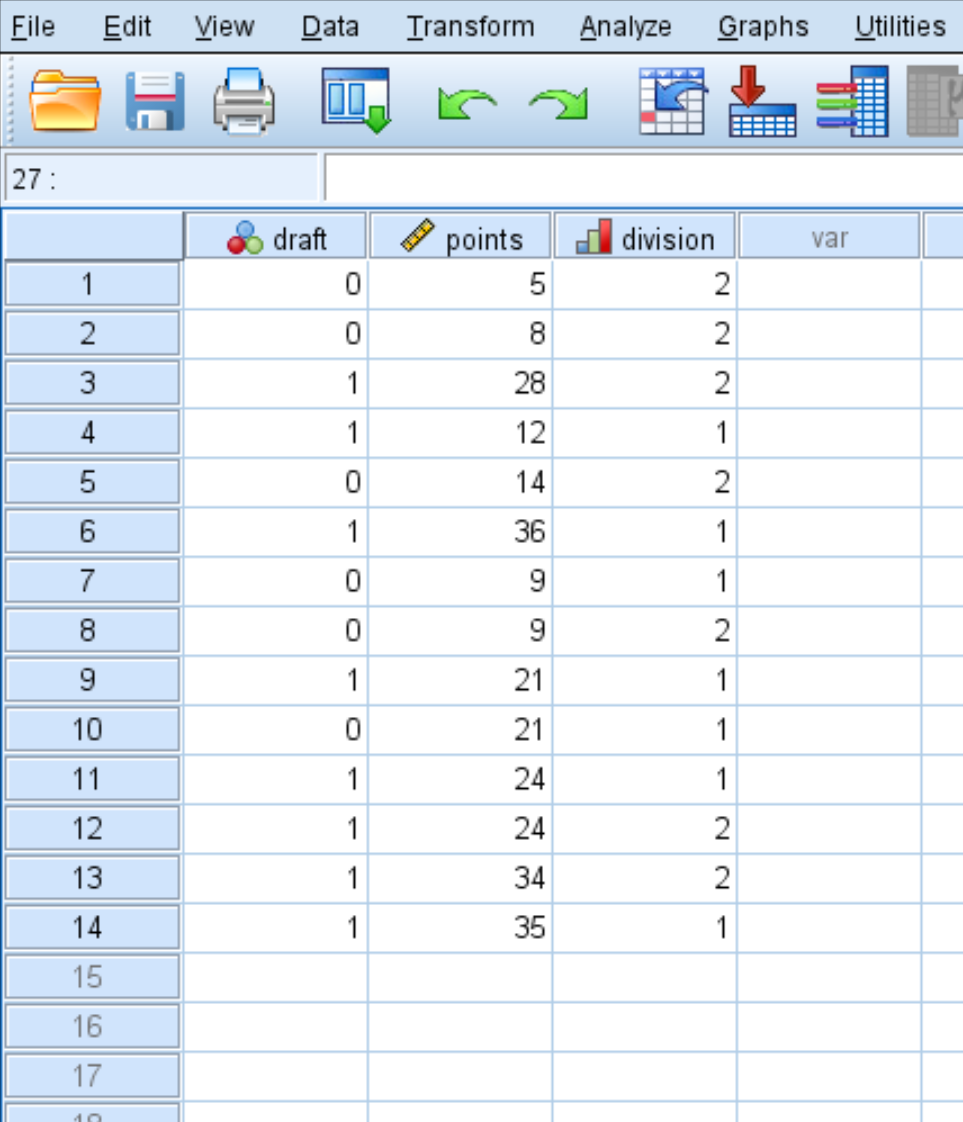
Stap 2: Voer logistische regressie uit.

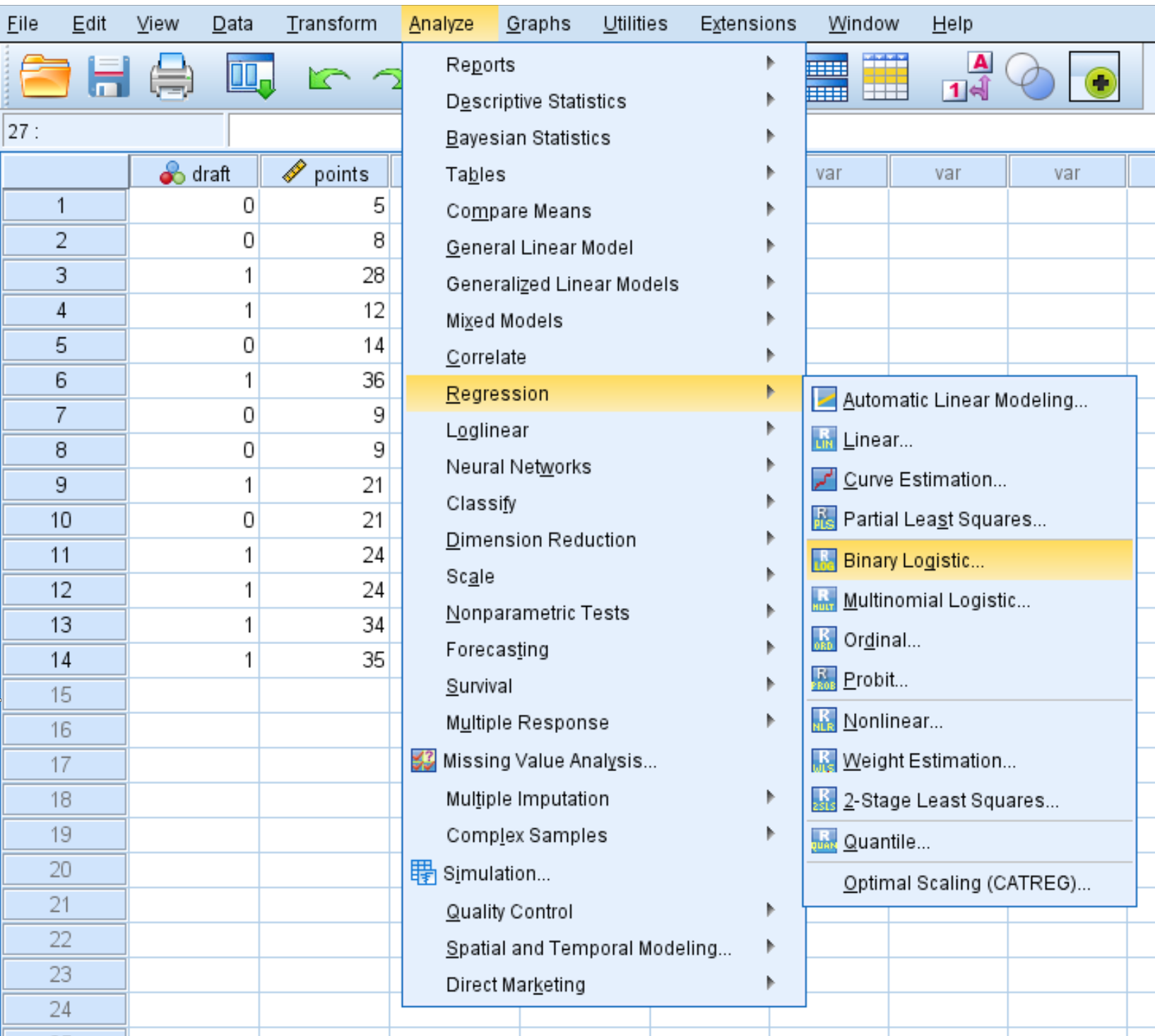
Klik op het tabblad Analyseren , vervolgens op Regressie en vervolgens op Binaire logistieke regressie :

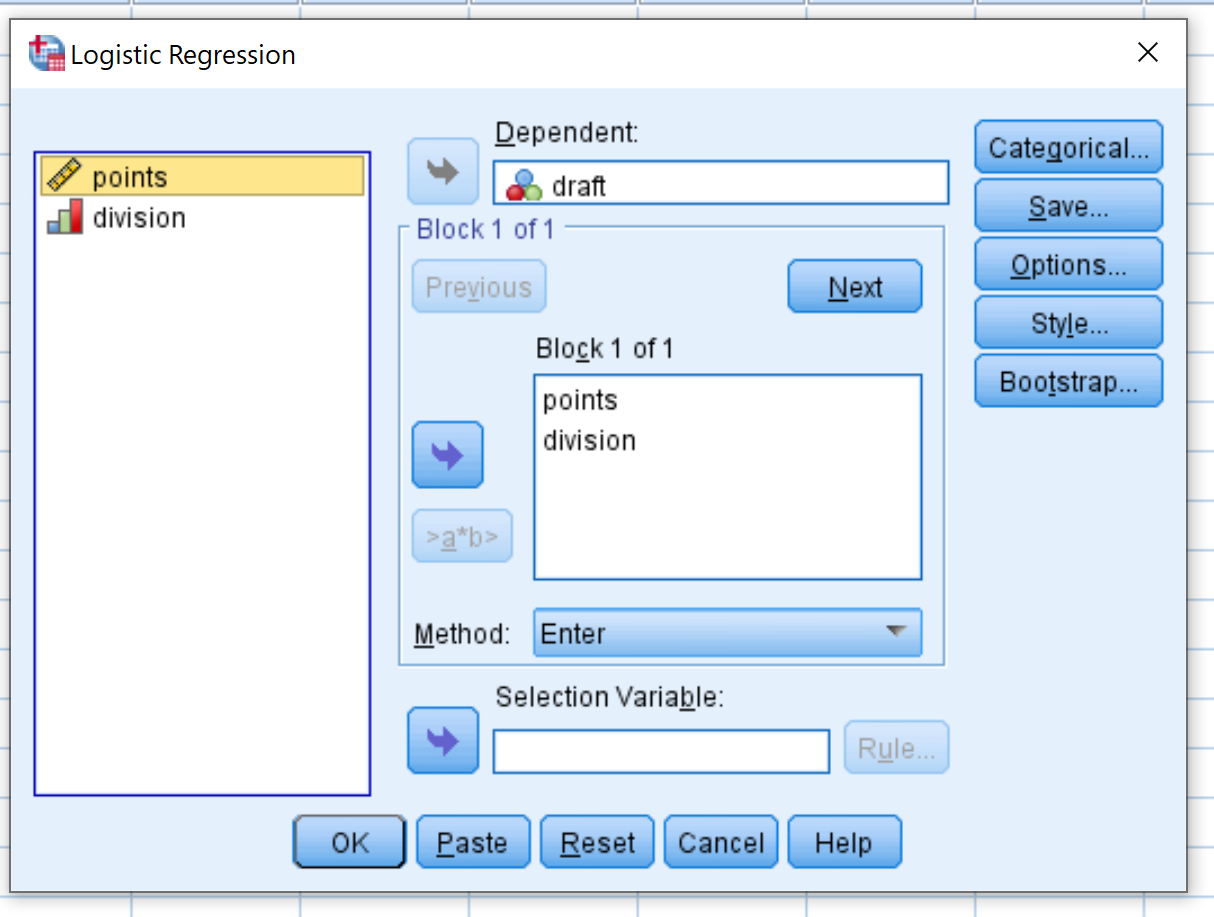
In het nieuwe venster dat verschijnt, sleept u het project van de binaire responsvariabele naar het gebied met de naam Dependent. Sleep vervolgens de dubbele punt en de deling van de voorspellende variabelen naar het vak met de naam Blok 1 van 1. Laat de methode ingesteld op Enter. Klik vervolgens op OK .

Stap 3. Interpreteer het resultaat.

Zodra u op OK klikt, verschijnt het logistische regressieresultaat:

Zo interpreteert u het resultaat:

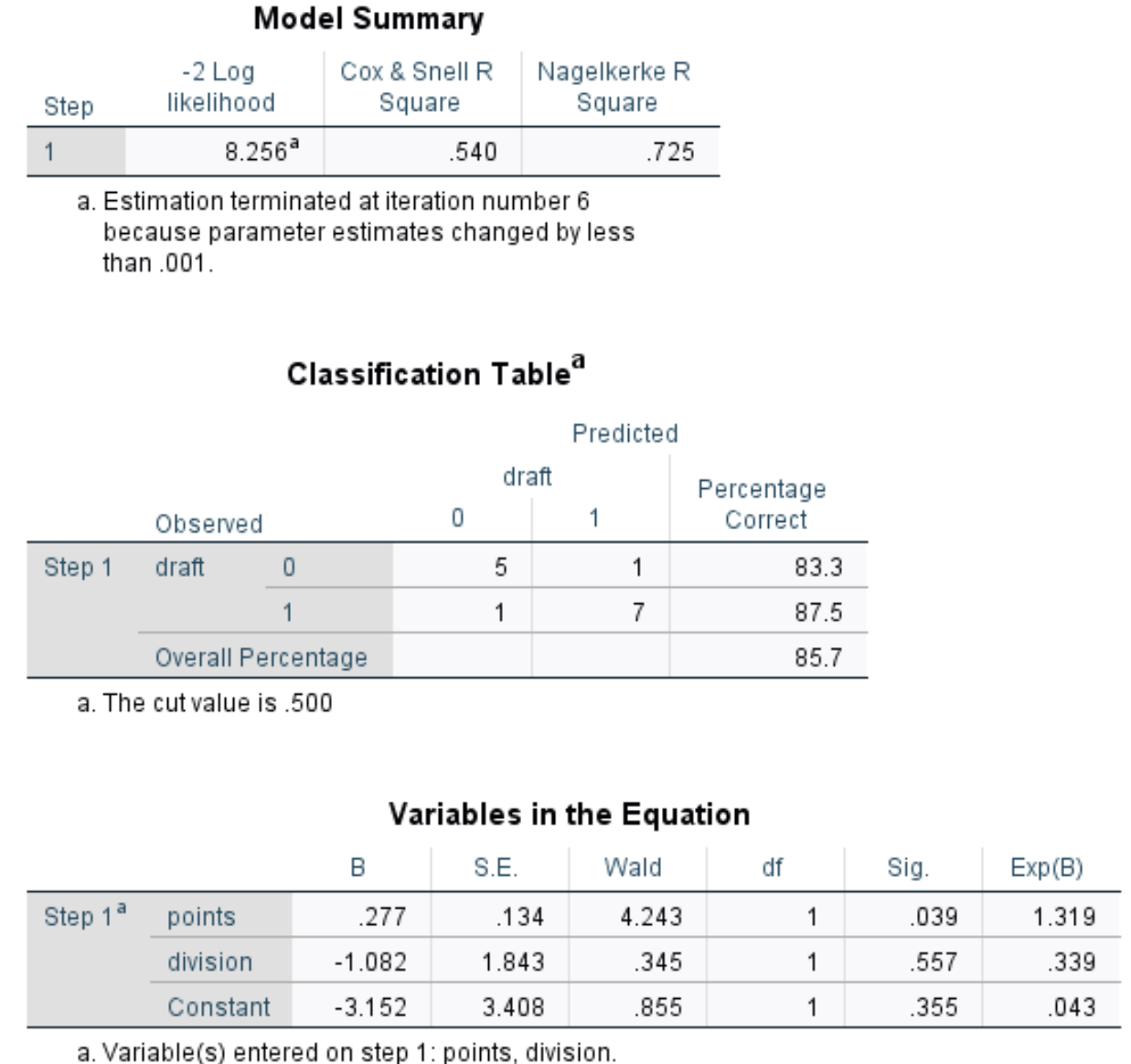
Modelsamenvatting: De nuttigste metriek in deze tabel is het Nagelkerke R-vierkant, dat ons het percentage variatie in de responsvariabele vertelt dat kan worden verklaard door de voorspellende variabelen. In dit geval kunnen punten en verdeling 72,5% van de diepgangvariabiliteit verklaren.

Classificatietabel: De nuttigste maatstaf in deze tabel is het totale percentage, dat ons vertelt welk percentage waarnemingen het model correct heeft kunnen classificeren. In dit geval kon het logistische regressiemodel de conceptuitkomst van 85,7% van de spelers correct voorspellen.

Variabelen in de vergelijking: Deze laatste tabel biedt ons verschillende nuttige metingen, waaronder:

• Wald: Wald-teststatistiek voor elke voorspellende variabele, die wordt gebruikt om te bepalen of elke voorspellende variabele statistisch significant is of niet.
• Sig: de p-waarde die overeenkomt met de Wald-teststatistiek voor elke voorspellende variabele. We zien dat de p-waarde voor punten 0,039 is en de p-waarde voor delen 0,557.
• Exp(B): de oddsratio voor elke voorspellende variabele. Dit vertelt ons de verandering in de kansen dat een speler wordt opgeroepen in verband met een toename van één eenheid in een bepaalde voorspellende variabele. De kans dat een speler uit Divisie 2 wordt opgeroepen, is bijvoorbeeld slechts 0,339 van de kans dat een speler uit Divisie 1 wordt opgeroepen. Op dezelfde manier wordt elke extra eenheidstoename in punten per spel geassocieerd met een toename van 1.319 in de kans dat een speler wordt opgeroepen.

We kunnen vervolgens de coëfficiënten (de waarden in de kolom met het label B) gebruiken om de waarschijnlijkheid te voorspellen dat een bepaalde speler wordt opgeroepen, met behulp van de volgende formule:

Waarschijnlijkheid = e ^{-3,152 + 0,277 (punten) – 1,082 (deling)} / (1+e ^{-3,152 + 0,277 (punten) – 1,082 (deling)} )

De kans dat een speler die gemiddeld 20 punten per wedstrijd behaalt en in Divisie 1 speelt, wordt opgeroepen, kan bijvoorbeeld als volgt worden berekend:

Waarschijnlijkheid = e ^{-3,152 + 0,277(20) – 1,082(1)} / (1+e ^{-3,152 + 0,277(20) – 1,082(1)} ) = 0,787 .

Omdat deze waarschijnlijkheid groter is dan 0,5, voorspellen we dat deze speler wordt opgeroepen.

Stap 4. Rapporteer de resultaten.

Ten slotte willen we de resultaten van onze logistische regressie rapporteren. Hier is een voorbeeld van hoe u dit kunt doen:

Er werd een logistieke regressie uitgevoerd om te bepalen hoe punten per spel en divisieniveau de kans beïnvloeden dat een basketbalspeler wordt opgeroepen. In totaal zijn bij de analyse 14 spelers gebruikt.

Het model verklaarde 72,5% van de variatie in projectresultaten en classificeerde 85,7% van de gevallen correct.

De kans dat een speler uit Divisie 2 wordt opgeroepen, was slechts 0,339 van de kans dat een speler uit Divisie 1 wordt opgeroepen.

Elke extra eenheidstoename in punten per spel ging gepaard met een toename van 1.319 in de kans dat een speler werd opgeroepen.