Hoe z-scores te berekenen in spss

Een z-score vertelt ons hoeveel standaarddeviaties een bepaalde waarde afwijkt van het gemiddelde.

De z-score van een gegeven waarde wordt als volgt berekend:

z-score = (x – μ) / σ

Goud:

• x: individuele waarde
• μ: populatiegemiddelde
• σ: standaarddeviatie van de populatie

In deze tutorial wordt uitgelegd hoe u z-scores berekent in SPSS.

Gerelateerd: Z-scores interpreteren

Hoe Z-scores te berekenen in SPSS

Stel dat we de volgende dataset hebben die het jaarinkomen (in duizenden) van 15 mensen weergeeft:

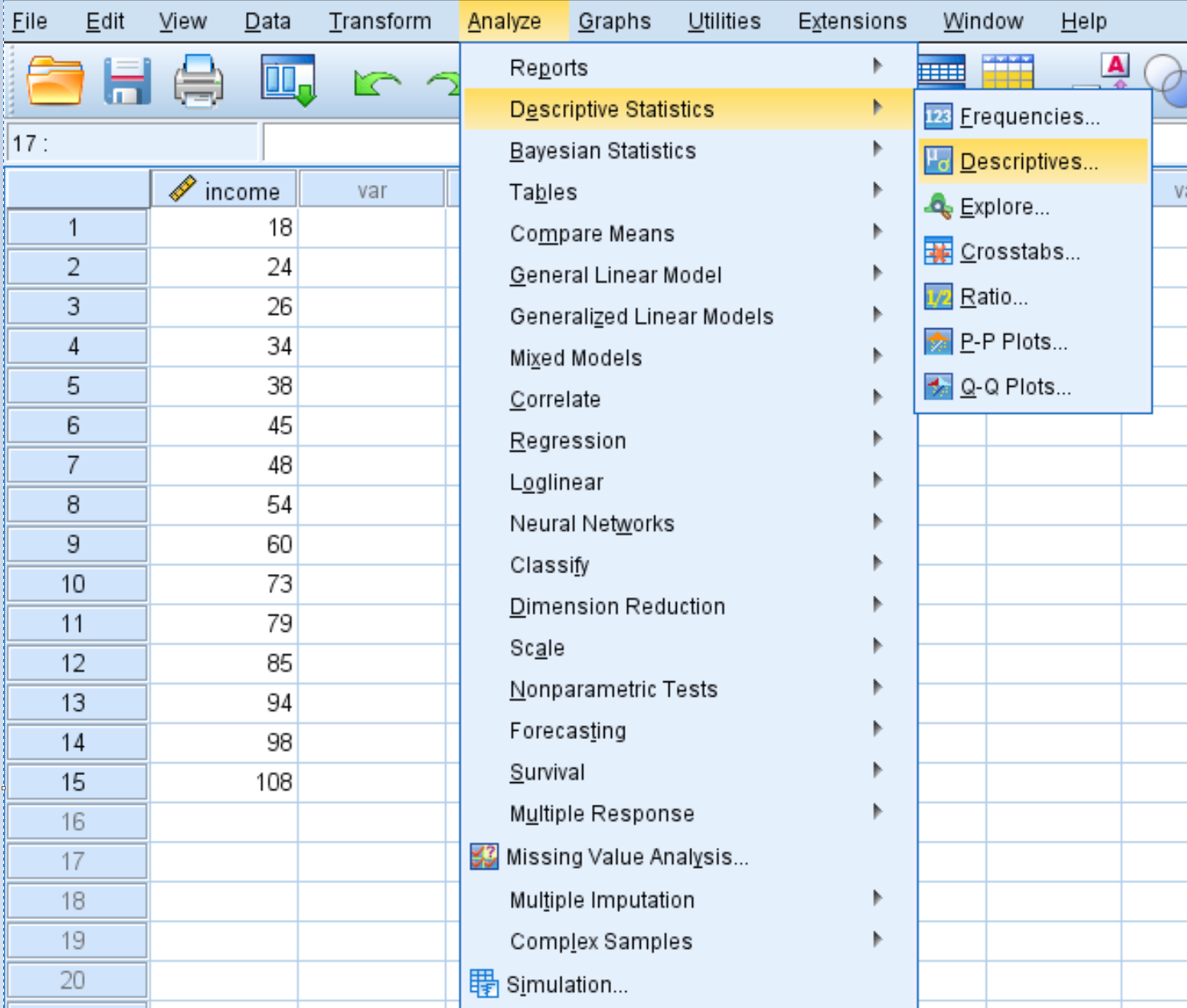
Om z-scores voor elke waarde in de dataset te berekenen, klikt u op het tabblad Analyseren , vervolgens op Beschrijvende statistieken en vervolgens op Beschrijvende gegevens :

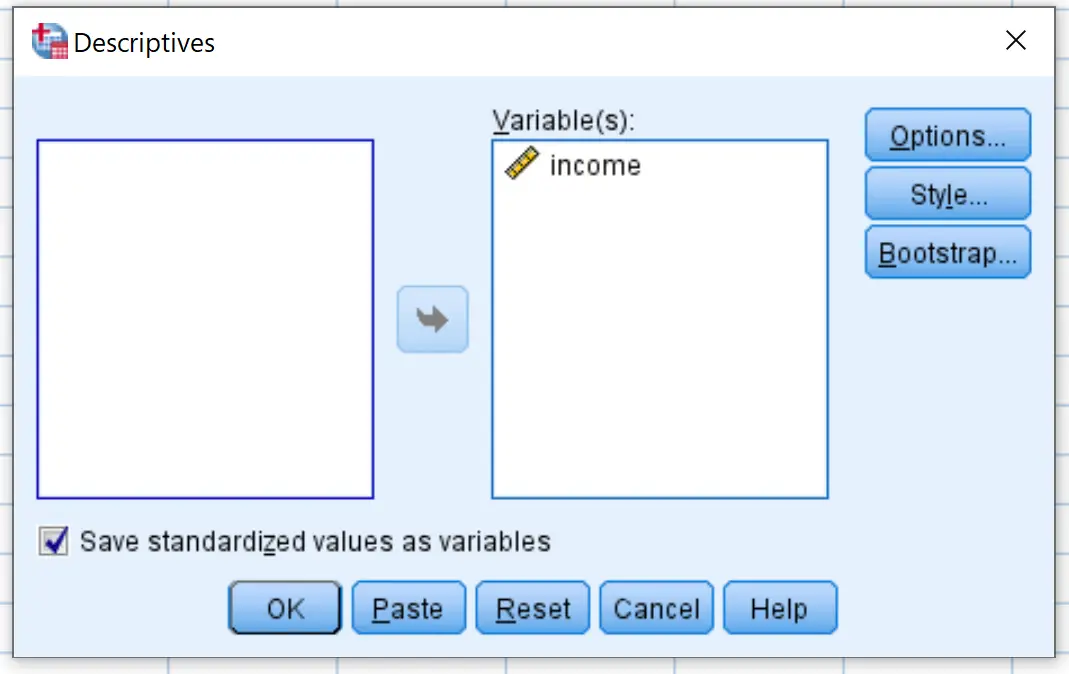
In het nieuwe venster dat verschijnt, sleept u de inkomensvariabele naar het vak met de naam Variabele(n).

Zorg ervoor dat het vakje naast Gestandaardiseerde waarden opslaan als variabelen is aangevinkt en klik vervolgens op OK .

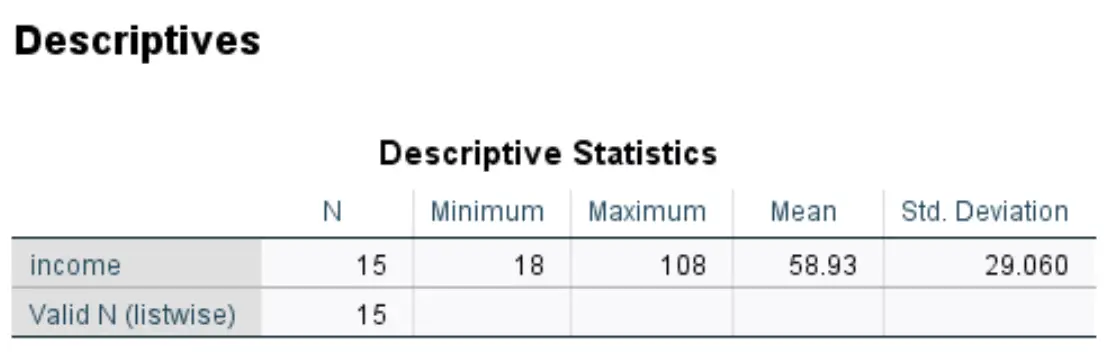
Zodra u op OK klikt, produceert SPSS een tabel met beschrijvende statistieken voor uw dataset:

SPSS zal ook een nieuwe kolom met waarden produceren die de z-score weergeeft voor elk van de oorspronkelijke waarden in uw dataset:

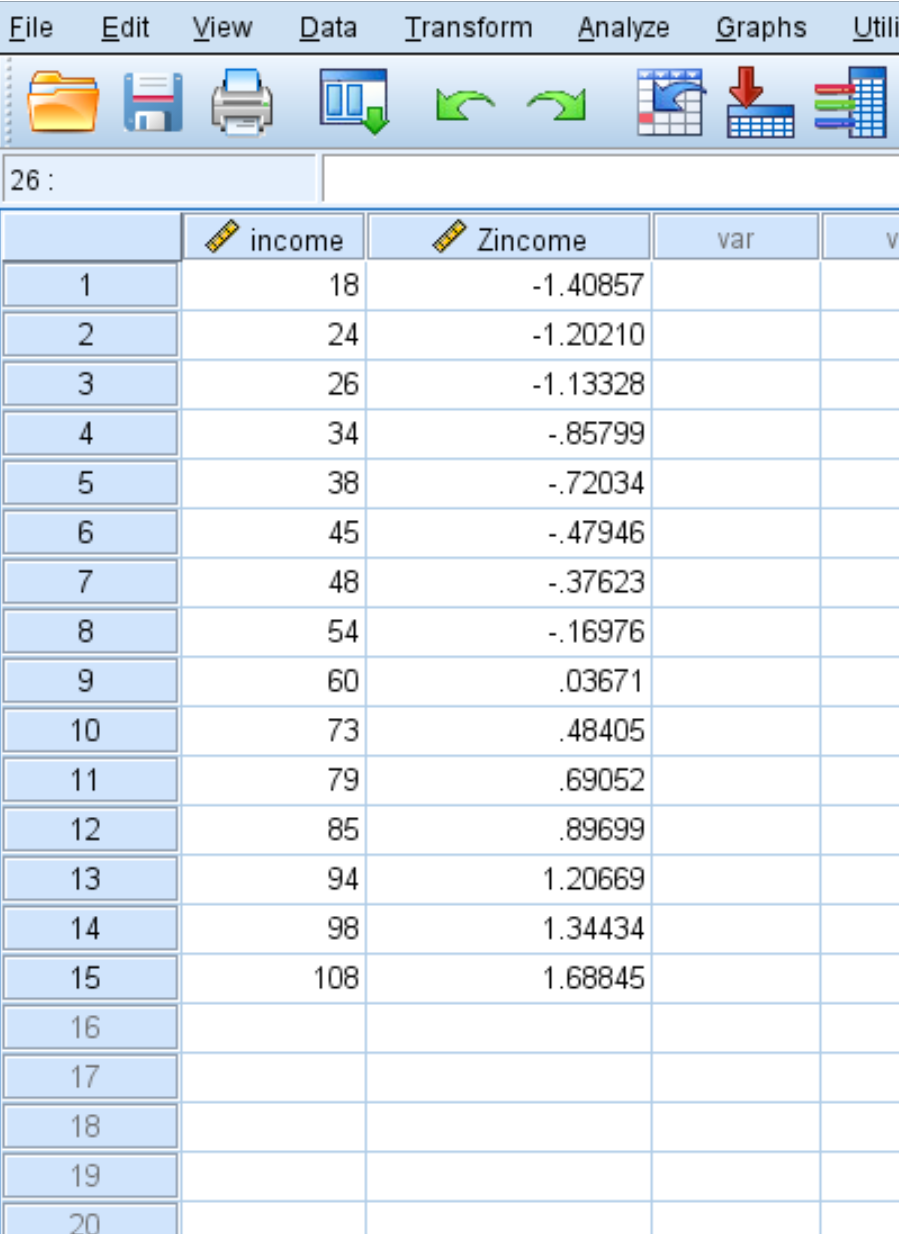
Elk van de z-scores wordt berekend met behulp van de formule z = (x – μ) / σ

De z-score voor de inkomenswaarde van 18 is bijvoorbeeld:

z = (18 – 58,93) / 29,060 = -1,40857 .

Z-scores voor alle andere gegevenswaarden worden op dezelfde manier berekend.

Hoe Z-scores te interpreteren

Bedenk dat een z-score ons eenvoudigweg vertelt hoeveel standaarddeviaties een waarde van het gemiddelde afwijkt.

Een z-score kan positief, negatief of gelijk aan nul zijn:

• Een positieve z-score geeft aan dat een bepaalde waarde boven het gemiddelde ligt.
• Een negatieve z-score geeft aan dat een bepaalde waarde onder het gemiddelde ligt.
• Een z-score van nul geeft aan dat een bepaalde waarde gelijk is aan het gemiddelde.

In ons voorbeeld ontdekten we dat het gemiddelde 58,93 was en de standaarddeviatie 29,060.

De eerste waarde in onze dataset was dus 18, die een z-score had van (18 – 58,93) / 29,060 = -1,40857 .

Dit betekent dat de waarde “18” 1,40857 standaarddeviaties lager is dan het gemiddelde.

Omgekeerd was de laatste waarde in onze gegevens 108, wat overeenkwam met een z-score van (108 – 58,93) / 29,060 = 1,68845 .

Dit betekent dat de waarde “108” 1,68845 standaarddeviaties boven het gemiddelde ligt.

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u andere veelvoorkomende taken in SPSS kunt uitvoeren:

Hoe beschrijvende statistieken voor variabelen in SPSS te berekenen
Hoe u een vijfcijferige samenvatting berekent in SPSS
Uitschieters identificeren in SPSS