Gini-index (of gini-coëfficiënt)

Von Dr.benjamin anderson August 5, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat de Gini-index, ook wel de Gini-coëfficiënt genoemd, is en waarvoor deze wordt gebruikt. Daarnaast vindt u een opgeloste oefening over het vinden van de Gini-index. Ten slotte kunt u de interpretatie van deze statistische metriek zien en wat de relatie is tussen de Gini-index en de Lorenz-curve.

Wat is de Gini-index?

De Gini-index , ook wel de Gini-coëfficiënt genoemd, is een statistische waarde die wordt gebruikt om de inkomensongelijkheid van een gebied te meten. Met andere woorden: de Gini-index geeft aan hoe gelijk een gebied is in de inkomensverdeling onder de bevolking.

De Gini-index is een getal tussen 0 en 1. Als de Gini-index 0 is, betekent dit dat de inkomensverdeling in het gebied zo eerlijk mogelijk is (perfecte gelijkheid), of met andere woorden: alle inwoners hebben hetzelfde inkomen. Aan de andere kant, als de Gini-coëfficiënt 1 is, komt dit overeen met perfecte ongelijkheid, dat wil zeggen dat één persoon alle inkomsten van het gebied heeft en de anderen niets ontvangen.

De Gini-index wordt gebruikt om de economische situatie tussen verschillende landen in de wereld te vergelijken, omdat deze het mogelijk maakt om de meest egalitaire landen en, omgekeerd, de meest ongelijke landen te vergelijken in termen van inkomensverdeling.

De Gini-index is uitgevonden door de beroemde statisticus Corrado Gini, vandaar de naam.

Hoe de Gini-index te berekenen

Gegeven de definitie van de Gini-index (of Gini-coëfficiënt), is hier hoe deze statistische maatstaf wordt berekend.

De formule voor de Gini-index (of Gini-coëfficiënt) is als volgt:

$\displaystyle G=\begin{vmatrix}\displaystyle 1-\sum_{k=1}^{n-1}(X_{k+1}-X_k)\cdot (Y_{k+1}+Y_k)\end{vmatrix}$

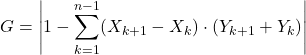
Goud:

$G$

is de Gini-index.
$X$

is het cumulatieve deel van de variabele populatie.
$Y$

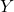
is het cumulatieve deel van de inkomensvariabele.

Zodat u precies kunt zien hoe de Gini-index wordt bepaald, is hieronder een stapsgewijs voorbeeld opgelost:

Bereken de Gini-index van de bevolking waarvan het inkomen in de volgende tabel wordt weergegeven.

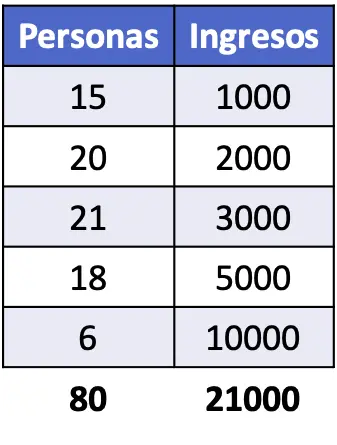
Om de Gini-coëfficiënt te vinden, moeten we het aandeel van elk inkomensniveau bepalen, evenals het cumulatieve aandeel. Bovendien moeten de berekeningen in de formule worden uitgevoerd om de waarde van de Gini-index te vinden.

Kortom, de volgende kolommen moeten aan de gegevenstabel worden toegevoegd:

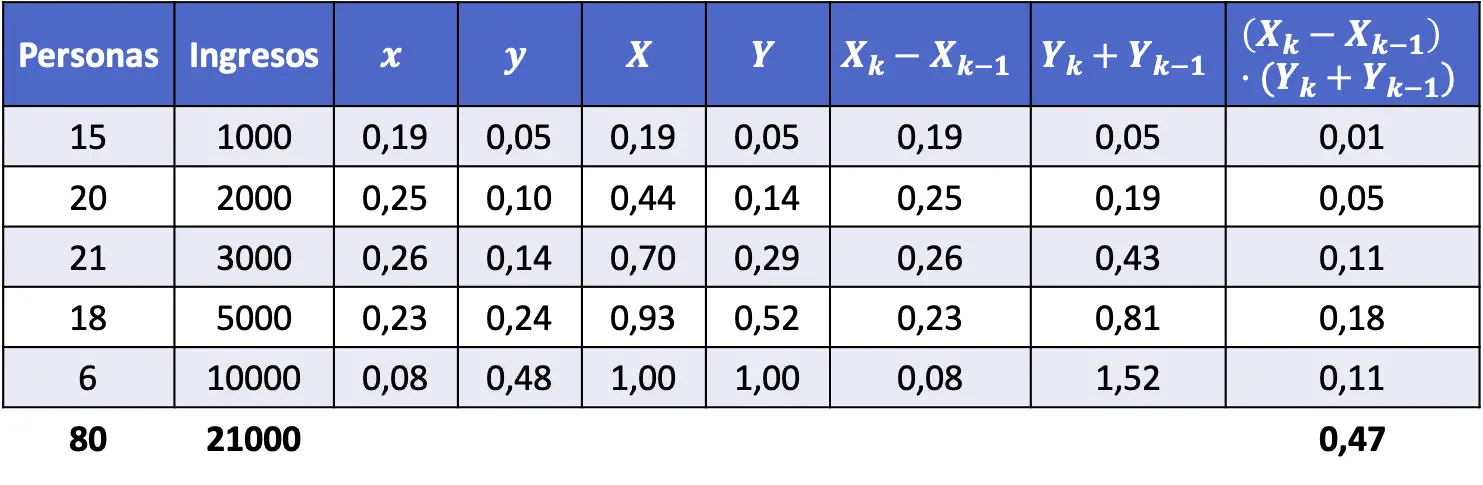
We gebruiken nu de Gini-indexformule:

$\displaystyle G=\begin{vmatrix}\displaystyle 1-\sum_{k=1}^{n-1}(X_{k+1}-X_k)\cdot (Y_{k+1}+Y_k)\end{vmatrix}$

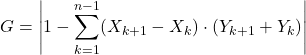
En ten slotte vervangen we de gegevens in de algebraïsche uitdrukking en berekenen we de Gini-coëfficiënt:

$\displaystyle G=\begin{vmatrix}\displaystyle 1-0,47\end{vmatrix}=0,53$

Verband tussen de Gini-index en de Lorenz-curve

In deze sectie zullen we zien hoe de Gini-index, ook bekend als de Gini-coëfficiënt, en de Lorenz-curve gerelateerd zijn.

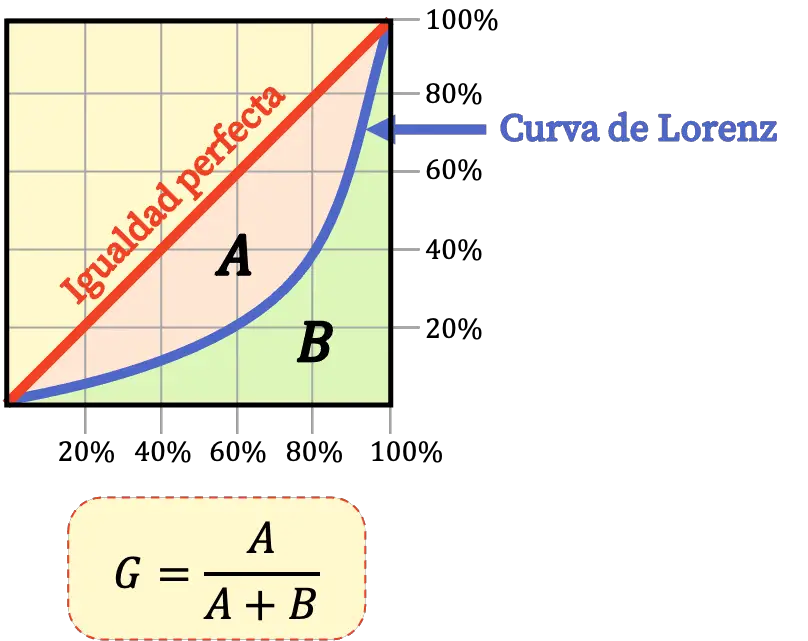
De Lorenz-curve is de grafische weergave van de economische ongelijkheid van de bevolking van een gebied. De Lorenz-curve geeft dus visueel de economische ongelijkheid van een bevolking aan.

Aan de andere kant is de Gini-index, zoals we hebben gezien, een waarde die wordt gebruikt om de ongelijkheden van een bevolking numeriek te beschrijven.

De Gini-index en de Lorenz-curve hebben dus hetzelfde doel : beide worden gebruikt om de economische ongelijkheid tussen de inwoners van een gebied te bepalen. De Gini-index evalueert de inkomensongelijkheid echter numeriek, terwijl de Lorenz-curve de economische ongelijkheid grafisch analyseert.

Bovendien kan de Gini-index worden berekend op basis van de gebieden die worden begrensd door de Lorenz-curve volgens de volgende formule:

relatie tussen de Gini-index en de Lorenz-curve

Interpretatie van de Gini-index

De waarde van de Gini-index kan variëren van 0 tot 1, beide inclusief. Hoe dichter de waarde van de Gini-coëfficiënt bij 0 ligt, dit betekent dat er meer economische gelijkheid in het gebied is. Aan de andere kant: hoe hoger de waarde van de Gini-index, hoe groter de ongelijkheid in de inkomensverdeling tussen de inwoners van een gebied.

De Gini-index zal dus gelijk zijn aan nul in een optimale situatie waarin alle inwoners exact hetzelfde inkomen hebben. Integendeel, de Gini-index zal 1 waard zijn wanneer het grondgebied een perfecte ongelijkheid vertoont, dat wil zeggen dat één enkele inwoner al het inkomen ontvangt en de rest van de inwoners geen inkomen heeft.

Landen met een grotere inkomensgelijkheid zijn dus landen met een lagere Gini-index. En de meest ongelijke landen hebben een zeer hoge Gini-index.

Zoals we hebben gezien, is de Gini-index gekoppeld aan de Lorenz-curve. Dus hoe lager de Gini-index, hoe dichter de Lorenz-curve bij de lijn van perfecte gelijkheid zal liggen. Hoe hoger de Gini-index, hoe meer kromming de Gini-curve zal hebben en dus hoe verder deze zal verwijderd zijn van de lijn die perfecte gelijkheid vertegenwoordigt.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder