Lorenz-curve

In dit artikel wordt uitgelegd wat de Lorenz-curve is en waarvoor deze wordt gebruikt. Je ontdekt hoe je de Lorenz-curve van een populatie kunt maken en bovendien kun je de oefening stap voor stap opgelost zien. Tenslotte worden de eigenschappen van de Lorenz-curve en de relatie met de Gini-index gepresenteerd.

Wat is de Lorenz-curve?

De Lorenz-curve is de grafische weergave van de economische ongelijkheid van de bevolking van een gebied. Met andere woorden: de Lorenz-curve is een curve die ons in staat stelt ongelijkheden in de inkomensverdeling over een gebied te analyseren.

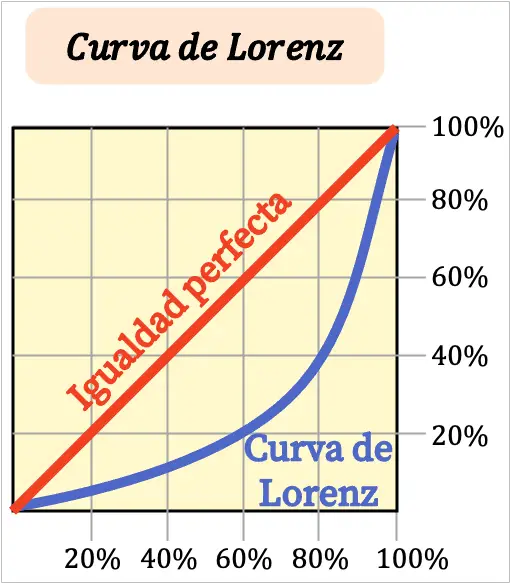
Hoe rechter de Lorenz-curve, hoe egalitairer het inkomen van het gebied. Aan de andere kant geldt dat hoe krommer de Lorenz-curve is, des te ongelijker de inkomens worden verdeeld.

Meestal worden de assen van de Lorenz-curve uitgedrukt als percentages. De X-as van de grafiek vertegenwoordigt het bevolkingspercentage en aan de andere kant toont de Y-as het inkomenspercentage.

De Lorenz-curve werd in 1905 uitgevonden door Max Otto Lorenz, een zeer belangrijke Amerikaanse econoom uit de 20e eeuw.

Hoe de Lorenz-curve te berekenen

Zodra we de definitie van de Lorenz-curve kennen, zullen we zien hoe deze statistische curve wordt berekend. Opgemerkt moet worden dat er een formule bestaat om de Lorenz-curve te definiëren, maar dat deze in de praktijk doorgaans niet wordt gebruikt. Daarom gaan we stap voor stap een voorbeeld oplossen, zodat je kunt zien hoe het moet.

• Vertegenwoordigt de Lorenz-curve van de bevolking waarvan het inkomen in de volgende tabel wordt weergegeven:

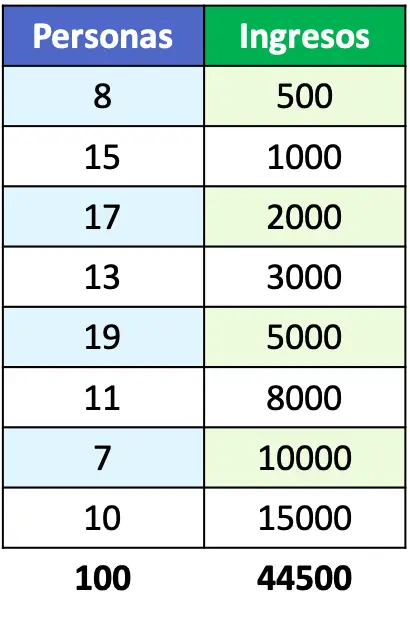
Als de probleemstelling ons het voorbeeld zou geven van een Lorenz-curvefunctie, zouden we de functie rechtstreeks in een grafiek kunnen weergeven. Maar in dit geval geven ze ons alleen het bevolkingsinkomen, dus moeten we het percentage van elke groep mensen berekenen.

Om de percentages van het aantal mensen en het inkomen te bepalen, moeten we dus twee kolommen aan de tabel toevoegen voor de populatievariabele:

• Een kolom met de geaccumuleerde absolute frequentie (Fi ₎ .
• Een tweede kolom die overeenkomt met het cumulatieve percentage, dat wordt berekend door de cumulatieve absolute frequentie te delen door het totale aantal personen.

En aan de andere kant moeten we drie kolommen toevoegen voor de inkomensvariabele:

• Kolom waarin het totale inkomen wordt berekend, gelijk aan het product van het aantal personen door het inkomen dat iedere persoon ontvangt.
• Een seconde met de geaccumuleerde absolute frequentie ( _Fi ) van het totale inkomen.
• Een derde kolom die het geaccumuleerde percentage bevat, bepaald door de vorige kolom te delen door het totale inkomen van de bevolking.

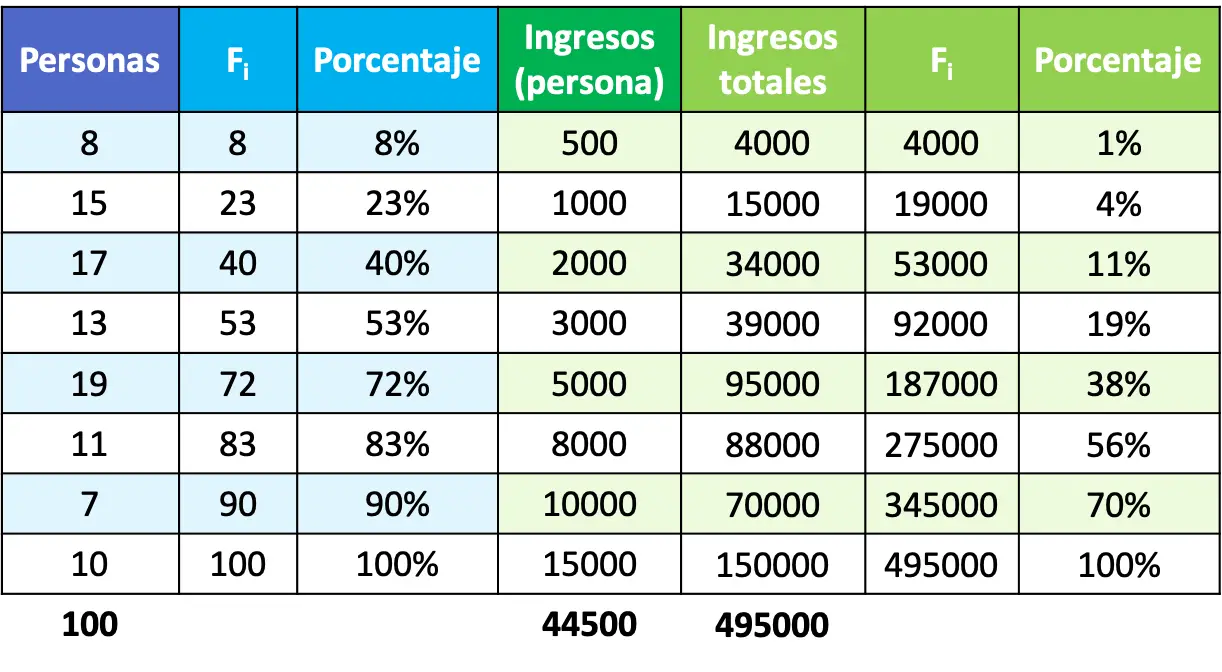
Nu we de percentages hebben berekend, hoeven we alleen nog maar de punten in een grafiek uit te zetten en ze samen te voegen om de Lorenz-curve te vormen. Houd er rekening mee dat de X-as het percentage van de bevolking is en de Y-as het percentage van het inkomen.

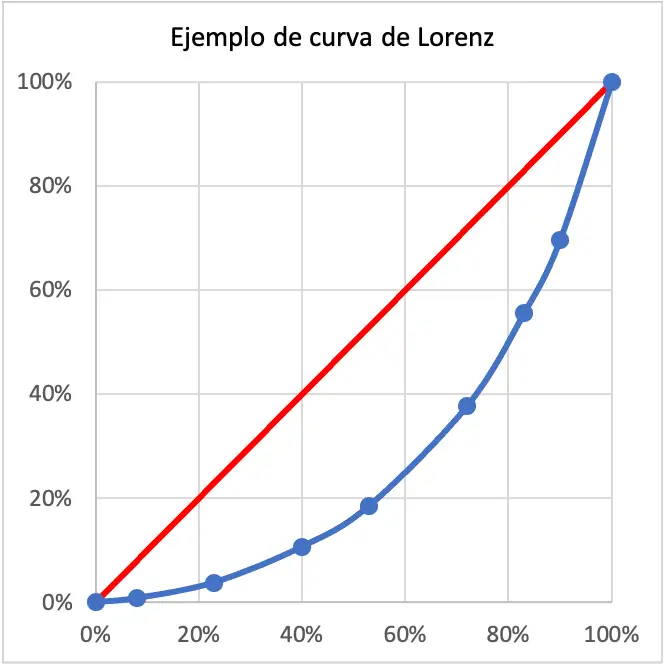
In dit geval is het inkomen van de bestudeerde bevolking zeer ongelijk, aangezien de Lorenz-curve erg breed is. In feite ligt de Lorenz-curve ver verwijderd van de rode lijn die perfecte gelijkheid vertegenwoordigt.

Interpretatie van de Lorenz-curve

In dit gedeelte wordt uitgelegd hoe u de Lorenz-curve van een populatie interpreteert, omdat u niet alleen weet hoe u deze in een grafiek moet weergeven, maar ook moet begrijpen wat deze betekent.

De Lorenz-curve geeft aan welk percentage van de bevolking een percentage van het totale inkomen van een gebied bezit. In het bovenstaande voorbeeld van de Lorenz-curve heeft bijvoorbeeld 40% van de bevolking een inkomen dat 11% van het totale bevolkingsinkomen bedraagt. Het is dus een zeer ongelijk terrein.

De Lorenz-curve vertegenwoordigt dus visueel de gelijkheid of ongelijkheid van inkomen tussen de inwoners van een land of gebied. Hoe verder we verwijderd raken van de lijn die volmaakte gelijkheid aangeeft, hoe meer dit betekent dat het inkomen van de bevolking ongelijker is. Aan de andere kant: hoe dichter de Lorenz-curve naar rechts komt, hoe meer dit impliceert dat het inkomen van de bevolking rechtvaardiger wordt verdeeld.

Bovendien, als de ene Lorenz-curve in de hele grafiek boven de andere Lorenz-curve ligt, betekent dit dat het inkomen van de eerste populatie gelijker is dan dat van de tweede.

Lorenz-curve en Gini-coëfficiënt

Zoals in het hele artikel wordt uitgelegd, laat de Lorenz-curve grafisch zien hoe het inkomen van een gebied wordt verdeeld en hoe ongelijk een gebied is.

Aan de andere kant geeft de Gini-coëfficiënt, ook wel Gini-index genoemd, numeriek de economische ongelijkheid van een gebied aan.

De Lorenz-curve en de Gini-coëfficiënt zijn dus met elkaar verbonden. De Gini-coëfficiënt van een land kan inderdaad worden berekend op basis van de Lorenz-curve. In het volgende artikel kun je zien hoe je dit doet:

Eigenschappen van de Lorenz-curve

De Lorenz-curve heeft de volgende eigenschappen:

• De Lorenz-curve begint altijd bij het punt (0,0) en eindigt bij (100,100).
• De Lorenz-curve is niet gedefinieerd als het steekproefgemiddelde nul is.
• De Lorenz-curve kan niet verschijnen in de grafiek boven de lijn van perfecte gelijkheid.
• Ervan uitgaande dat het inkomen niet negatief kan zijn, stijgt de Lorenz-curve altijd.