Curve-aanpassing in r (met voorbeelden)

Vaak wil je misschien de vergelijking vinden die het beste bij een curve van R past.

In het volgende stapsgewijze voorbeeld wordt uitgelegd hoe u curven aan gegevens in R kunt aanpassen met behulp van de functie poly() en hoe u kunt bepalen welke curve het beste bij de gegevens past.

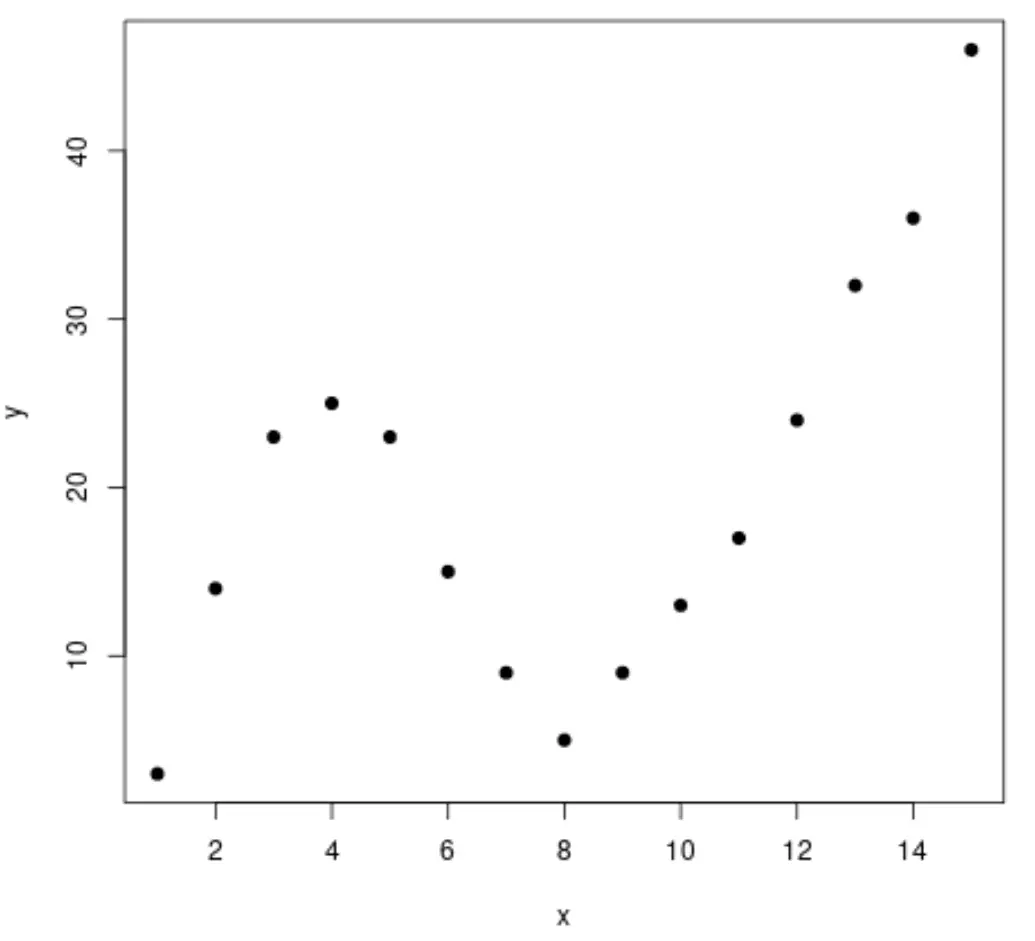
Stap 1: Gegevens creëren en visualiseren

Laten we beginnen met het maken van een nepgegevensset en vervolgens een spreidingsdiagram maken om de gegevens te visualiseren:

 #create data frame
df <- data. frame (x=1:15,
                 y=c(3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46))

#create a scatterplot of x vs. y
plot(df$x, df$y, pch= 19 , xlab=' x ', ylab=' y ') 

Stap 2: Pas meerdere curven aan

Laten we vervolgens verschillende polynomiale regressiemodellen aan de gegevens aanpassen en de curve van elk model in dezelfde plot visualiseren:

 #fit polynomial regression models up to degree 5
fit1 <- lm(y~x, data=df)
fit2 <- lm(y~poly(x,2,raw= TRUE ), data=df)
fit3 <- lm(y~poly(x,3,raw= TRUE ), data=df)
fit4 <- lm(y~poly(x,4,raw= TRUE ), data=df)
fit5 <- lm(y~poly(x,5,raw= TRUE ), data=df)

#create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of each model to plot
lines(x_axis, predict(fit1, data. frame (x=x_axis)), col=' green ')
lines(x_axis, predict(fit2, data. frame (x=x_axis)), col=' red ')
lines(x_axis, predict(fit3, data. frame (x=x_axis)), col=' purple ')
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')
lines(x_axis, predict(fit5, data. frame (x=x_axis)), col=' orange ')

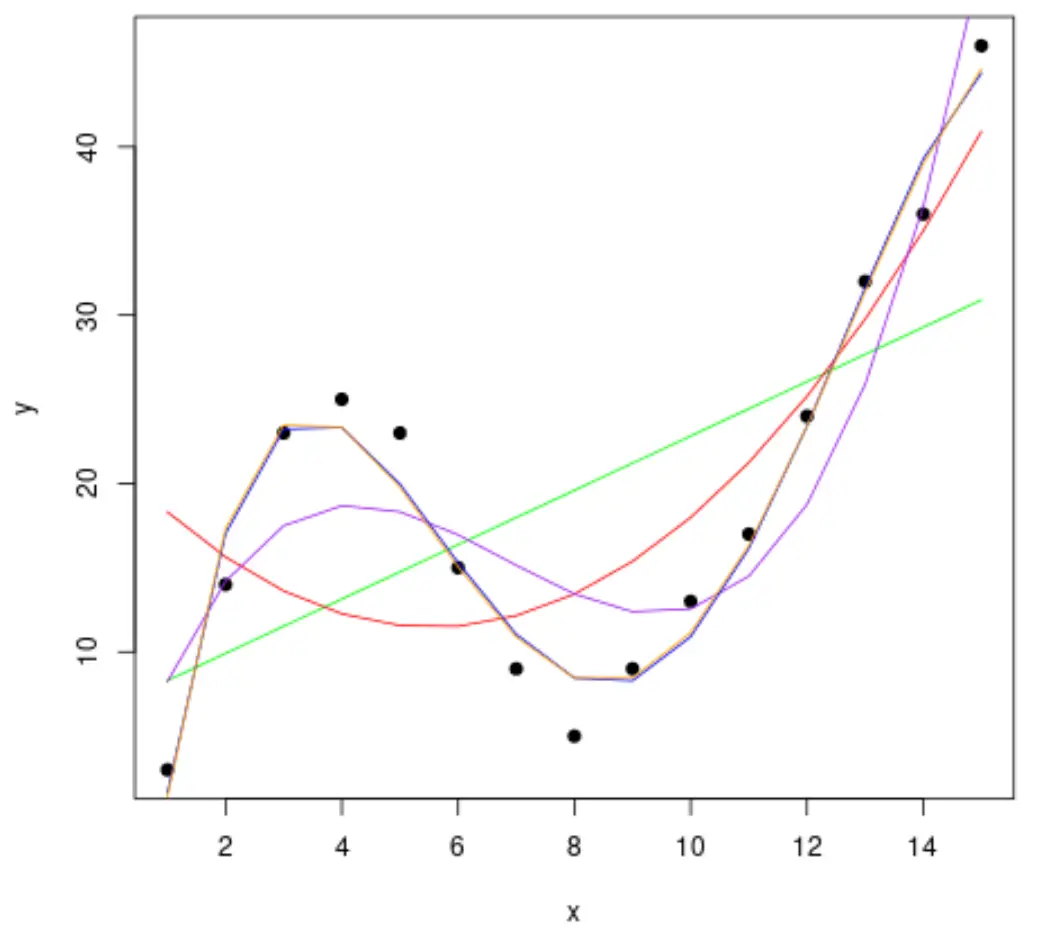
Om te bepalen welke curve het beste bij de gegevens past, kunnen we naar het aangepaste R-kwadraat van elk model kijken.

Deze waarde vertelt ons het percentage variatie in de responsvariabele dat kan worden verklaard door de voorspellende variabele(n) in het model, aangepast voor het aantal voorspellende variabelen.

 #calculated adjusted R-squared of each model
summary(fit1)$adj. r . squared
summary(fit2)$adj. r . squared
summary(fit3)$adj. r . squared
summary(fit4)$adj. r . squared
summary(fit5)$adj. r . squared

[1] 0.3144819
[1] 0.5186706
[1] 0.7842864
[1] 0.9590276
[1] 0.9549709

Uit het resultaat kunnen we zien dat het model met de hoogst aangepaste R-kwadraat de vierdegraads polynoom is, die een aangepaste R-kwadraat van 0,959 heeft.

Stap 3: Visualiseer de uiteindelijke curve

Ten slotte kunnen we een spreidingsdiagram maken met de curve van het vierdegraads polynoommodel:

 #create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of fourth-degree polynomial model
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')

We kunnen ook de vergelijking voor deze regel verkrijgen met behulp van de summary() functie:

 summary(fit4)

Call:
lm(formula = y ~ poly(x, 4, raw = TRUE), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-3.4490 -1.1732 0.6023 1.4899 3.0351 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) -26.51615 4.94555 -5.362 0.000318 ***
poly(x, 4, raw = TRUE)1 35.82311 3.98204 8.996 4.15e-06 ***
poly(x, 4, raw = TRUE)2 -8.36486 0.96791 -8.642 5.95e-06 ***
poly(x, 4, raw = TRUE)3 0.70812 0.08954 7.908 1.30e-05 ***
poly(x, 4, raw = TRUE)4 -0.01924 0.00278 -6.922 4.08e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.424 on 10 degrees of freedom
Multiple R-squared: 0.9707, Adjusted R-squared: 0.959 
F-statistic: 82.92 on 4 and 10 DF, p-value: 1.257e-07

De vergelijking van de curve is als volgt:

y = -0,0192x ⁴ + 0,7081x ³ – 8,3649x ² + 35,823x – 26,516

We kunnen deze vergelijking gebruiken om de waarde van deresponsvariabele te voorspellen op basis van de voorspellende variabelen in het model. Als x = 4 bijvoorbeeld, voorspellen we dat y = 23,34 :

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,3649(4) ² + 35,823(4) – 26,516 = 23,34

Aanvullende bronnen

Een inleiding tot polynomiale regressie
Polynomiale regressie in R (stap voor stap)
Hoe de seq-functie in R te gebruiken