Absolute frequentie

Dit artikel legt de betekenis van absolute frequentie in statistieken uit. Zo ontdek je hoe je de absolute frequentie van een dataset kunt verkrijgen, twee opgeloste oefeningen en bovendien de verschillen met andere soorten statistische frequenties.

Wat is de absolute frequentie?

In de statistiek is de absolute frequentie het aantal keren dat een waarde in een dataset voorkomt. Simpel gezegd is de absolute frequentie het aantal keren dat een resultaat wordt herhaald.

Als zeven mensen in een enquête bijvoorbeeld antwoorden dat hun favoriete kleur rood is, dan is de absolute frequentie van de kleur rood 7.

Daarom is de som van de absolute frequenties van alle waarden gelijk aan het totale aantal gegevens in de statistische steekproef.

Over het algemeen wordt de letter f met subscript i gebruikt om de absolute frequentie van de waarde i weer te geven, dus het symbool voor absolute frequentie is _fi .

Hoe de absolute frequentie te berekenen

Om de absolute frequenties van een dataset te verkrijgen, moet u de volgende stappen volgen:

1. Als de variabele discreet is, maak dan een array van alle verschillende waarden die in de dataset voorkomen, dat wil zeggen: plaats elke verschillende waarde in een rij van een tabel.
2. Als de variabele continu is, groepeert u de gegevens in intervallen en maakt u een tabel met alle intervallen.
3. Tel het aantal keren dat een waarde in de dataset voorkomt en noteer het resultaat in de frequentietabel.
4. Herhaal de vorige stap voor elke verschillende waarde in de voorbeeldgegevens.

Absolute frequentievoorbeelden

Zodra we de definitie van absolute frequentie hebben gezien en de theorie over hoe deze wordt berekend, gaan we twee voorbeelden bekijken, zodat u begrijpt hoe dit wordt gedaan. In het eerste voorbeeld zullen we de absolute frequenties van een discrete variabele bepalen en in het tweede voorbeeld van een continue variabele, aangezien de procedure enigszins varieert afhankelijk van het geval.

Voorbeeld 1: discrete variabele

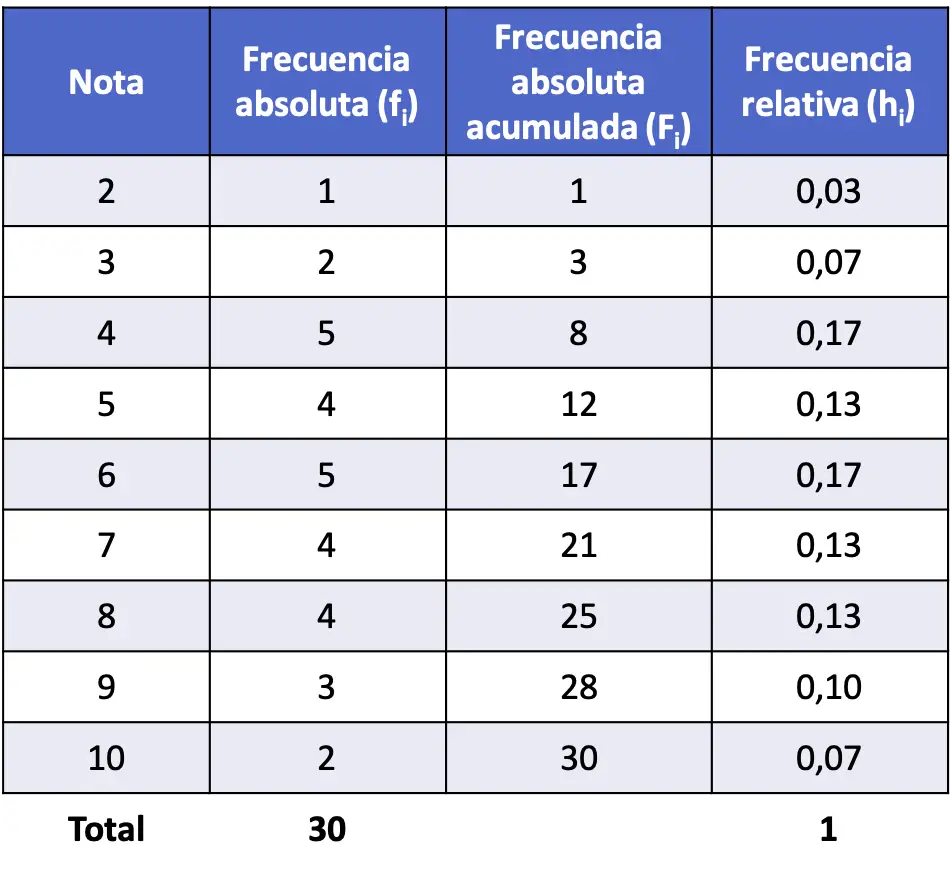
• De cijfers behaald in de statistiek in een klas van 30 studenten zijn als volgt. Wat is de absolute frequentie van elke noot?

In dit geval is het een discrete variabele omdat er alleen gehele getallen kunnen zijn, dus het is niet nodig om ze in intervallen te groeperen.

Tel dus gewoon hoe vaak elke waarde verschijnt en schrijf deze in een frequentietabel:

Merk op dat de som van alle absolute frequenties gelijk is aan het totale aantal datapunten. Als deze regel niet wordt gevolgd, betekent dit dat u een aantal gegevens bent vergeten te tellen.

Voorbeeld 2: continue variabele

• De lengte van 20 personen werd gemeten en de onderstaande resultaten werden verkregen. Verdeel de gegevens in intervallen en vind de absolute frequentie van elk interval.

De gegevens in dit voorbeeld volgen een continue verdeling, omdat getallen decimaal kunnen zijn. Daarom moeten we de gegevens in intervallen groeperen, in dit geval zullen we intervallen maken met een breedte van 10 tienden.

We tellen dus het aantal gegevens in elk interval en vertegenwoordigen de absolute frequenties in een tabel:

Absolute frequentie en cumulatieve absolute frequentie

Zoals de naam al doet vermoeden, is cumulatieve absolute frequentie een ander type frequentie dat in statistieken wordt gebruikt en verband houdt met absolute frequentie.

De cumulatieve absolute frequentie van een waarde is gelijk aan de som van de absolute frequentie van de waarde zelf plus de absolute frequenties van alle voorgaande waarden.

Als voorbeeld kun je hieronder de berekening zien van de geaccumuleerde absolute frequenties van de eerste oefening die hierboven is opgelost:

Absolute frequentie en relatieve frequentie

In statistieken is relatieve frequentie een ander type frequentie dan de twee hierboven gezien, omdat het het percentage van elke waarde vertegenwoordigt vergeleken met het totaal. Daarom zullen we in deze sectie het verschil tussen deze twee concepten zien.

Het verschil tussen absolute frequentie en relatieve frequentie is dat absolute frequentie het absolute aantal waarden in een monster is, terwijl relatieve frequentie de verhouding is van elke waarde tot het totaal.

Daarom wordt de relatieve frequentie berekend door de absolute frequentie te delen door het totale aantal gegevens.