Hoe aic in sas te berekenen (met voorbeeld)

Het Akaike Information Criterion (AIC) is een maatstaf die wordt gebruikt om de fit van meerdere regressiemodellen te vergelijken.

Het wordt als volgt berekend:

AIC = 2K – 2 ln (L)

Goud:

• K: Het aantal modelparameters. De standaardwaarde van K is 2, dus een model met slechts één voorspellende variabele heeft een K-waarde van 2+1 = 3.
• ln (L) : De log-waarschijnlijkheid van het model. De meeste statistische software kan deze waarde automatisch voor u berekenen.

AIC is ontworpen om het model te vinden dat de meeste variatie in de gegevens verklaart, terwijl modellen worden bestraft die een buitensporig aantal parameters gebruiken.

Nadat u meerdere regressiemodellen heeft geïnstalleerd, kunt u de AIC-waarde van elk model vergelijken. Hoe lager de AIC, hoe geschikter het model.

In het volgende voorbeeld ziet u hoe u AIC kunt berekenen voor verschillende regressiemodellen in SAS.

Voorbeeld: Hoe AIC in SAS te berekenen

Stel dat we drie verschillende meervoudige lineaire regressiemodellen willen toepassen om te voorspellen welk examencijfer studenten in een klas zullen behalen.

Dit zijn de voorspellende variabelen die we in elk model zullen gebruiken:

• Voorspellende variabelen in model 1: uren besteed aan studeren
• Voorspellende variabelen in model 2: praktijkexamens uit het verleden
• Voorspellende variabelen in Model 3: uren besteed aan studeren en afgelegde oefenexamens

Eerst gebruiken we de volgende code om een dataset te maken met deze informatie voor 20 studenten:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Vervolgens zullen we proc reg gebruiken om elk van deze regressiemodellen aan te passen en zullen we de instructie Selection=adjrsq sse aic gebruiken om de AIC-waarden voor elk model te berekenen:

 /*fit multiple linear regression models and calculate AIC for each model*/
proc reg data =exam_data;
    model score = hours prep_exams / selection=adjrsq sse aic;
run ; 

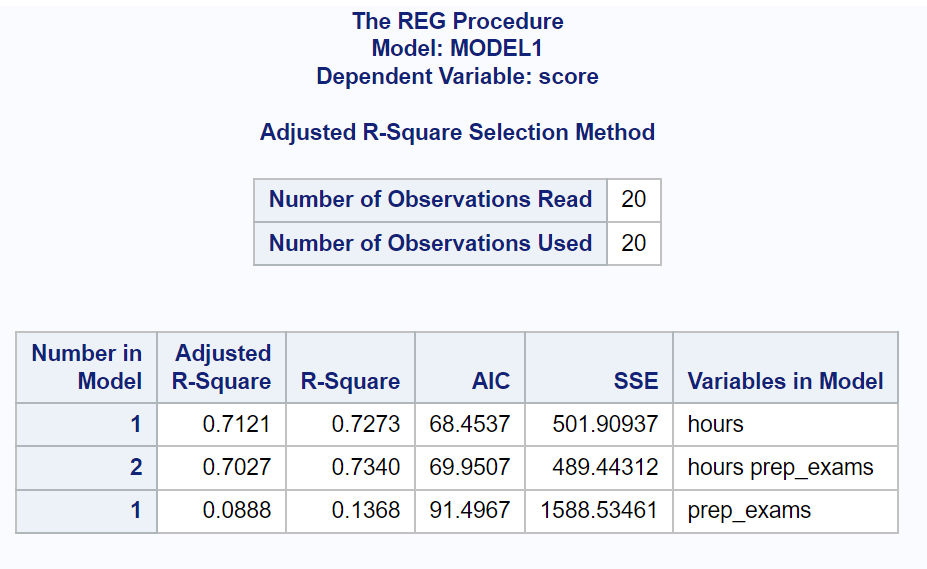
Uit het resultaat kunnen we de AIC-waarden voor elk model zien:

• AIC met uren als voorspellende variabele: 68,4537
• AIC met uren en examens als voorspellende variabelen: 69,9507
• AIC met examens als voorspellende variabele: 91,4967

Het model met de laagste AIC-waarde is het model dat alleen uren als voorspellende variabele bevat.

We verklaren dus dat het volgende model het beste bij de gegevens past:

Score = β ₀ + β ₁ (uren bestudeerd)

Zodra we dit model als het beste hebben geïdentificeerd, kunnen we het aanpassen en de resultaten analyseren, inclusief de R-kwadraatwaarde en bètacoëfficiënten, om de exacte relatie tussen het aantal bestudeerde uren en het cijfer van de student te bepalen. ‚eindexamen.

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in SAS kunt uitvoeren:

Hoe u eenvoudige lineaire regressie uitvoert in SAS
Hoe u meerdere lineaire regressie uitvoert in SAS
Hoe R-kwadraat in SAS te berekenen
Hoe RMSE in SAS te berekenen