Hoe alpha/2 t-waarden te vinden

Telkens wanneer je de term t _α/2 tegenkomt in de statistieken, verwijst deze eenvoudigweg naar de kritische waarde t van de t-verdelingstabel die overeenkomt met α/2.

In deze zelfstudie wordt het volgende uitgelegd:

• Hoe t _α/2 te vinden met behulp van de az-tabel.
• Hoe t _α/2 te vinden met behulp van een rekenmachine.
• Hoe t _α/2 -waarden te gebruiken.

Laten we gaan!

Hoe u t _α/2 kunt vinden met behulp van aan tafel

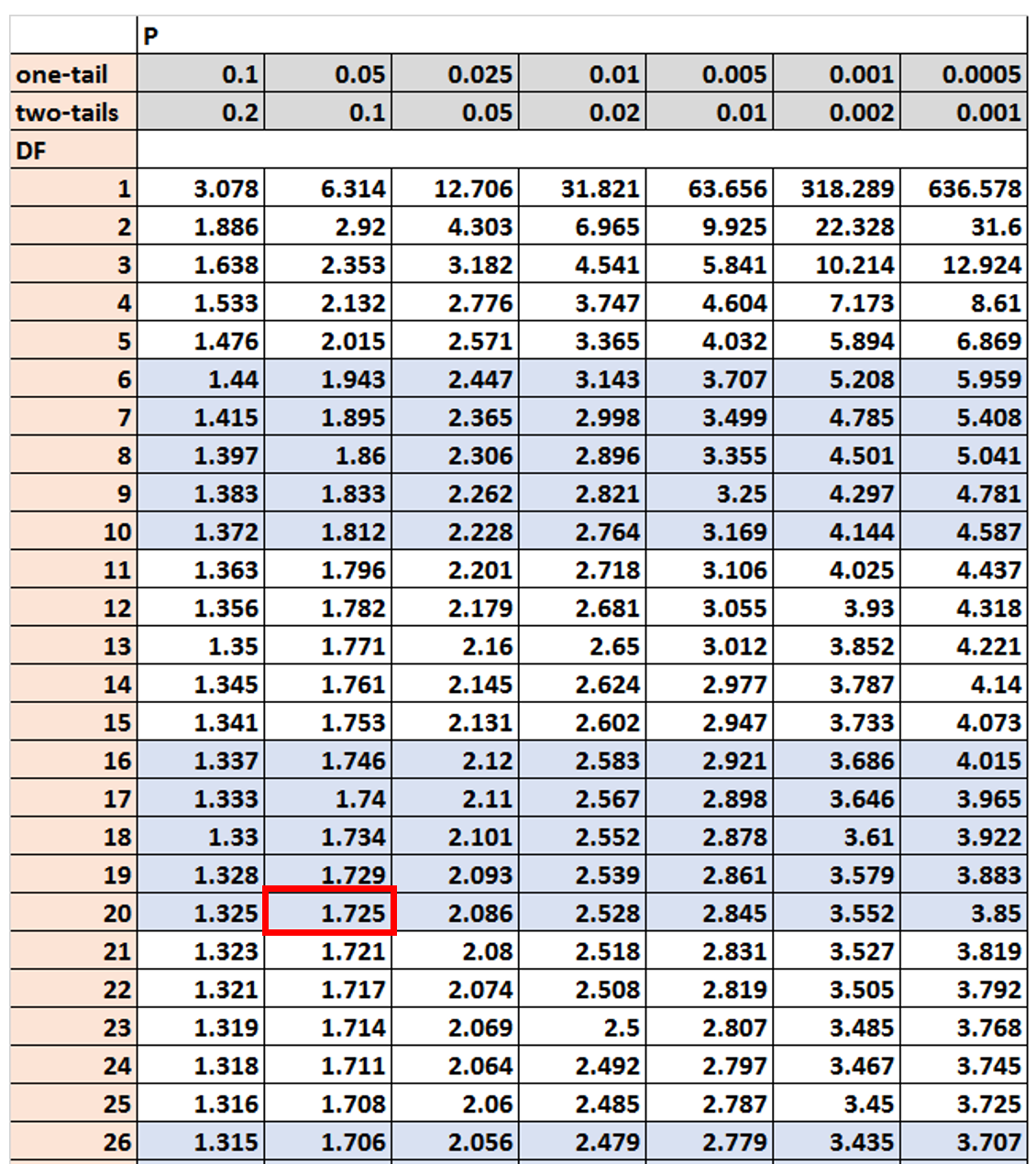
Stel dat we t _α/2 willen vinden voor een test met behulp van de volgende waarden:

• Alfaniveau: 0,10
• Testtypen: Bilateraal
• Vrijheidsgraden: 20

Met behulp van een t-verdelingstabel kunnen we ontdekken dat de kritische t-waarde 1,725 is:

Hoe t _α/2 te vinden met behulp van een rekenmachine

We kunnen voor sommige tests ook de inverse t-verdelingscalculator gebruiken om t _α/2 te vinden.

Stel dat we bijvoorbeeld opnieuw t _α/2 willen vinden voor een test met behulp van de volgende waarden:

• Alfaniveau: 0,10
• Testtypen: Bilateraal
• Vrijheidsgraden: 20

We kunnen de volgende waarden in de rekenmachine invoeren en ontdekken dat de kritische waarde t 1,7247 is:

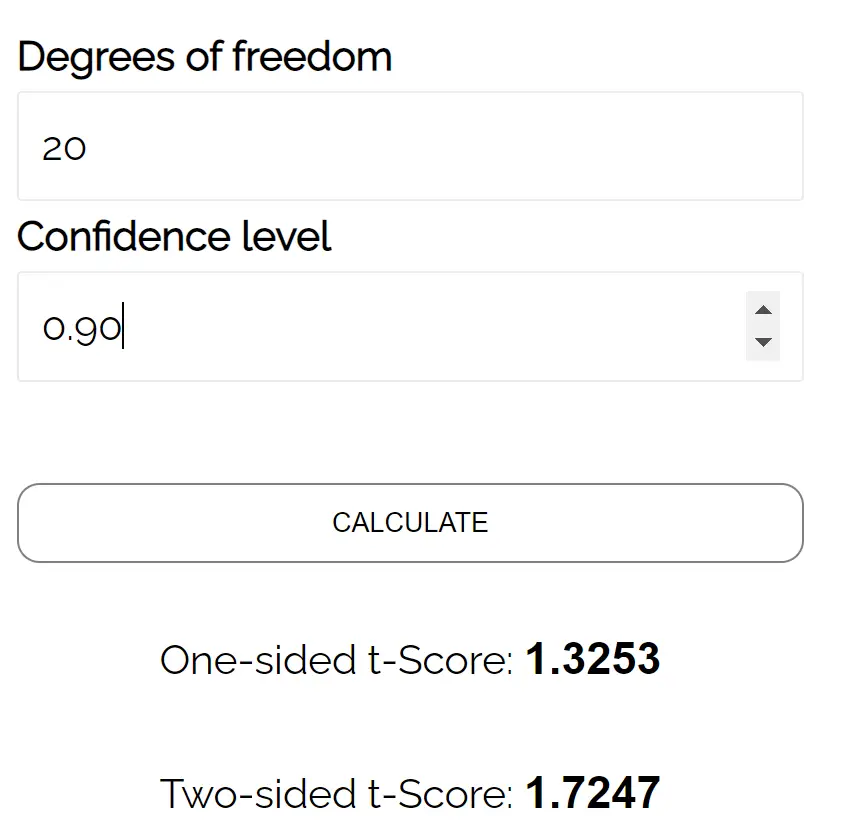
Dit komt overeen met de kritische waarde t die we in de t-verdelingstabel hebben gevonden.

Hoe t _α/2 -waarden te gebruiken

In de praktijk worden bij het testen van hypothesen kritische t-waarden gebruikt om te bepalen of de resultaten van een test statistisch significant zijn.

Het basisproces om dit te doen is:

Stap 1: Bereken de teststatistiek met behulp van onbewerkte gegevens.

Stap 2: Vergelijk de teststatistiek met de kritische waarde t (t _α/2 ).

Stap 3: Verwerp de nulhypothese van de test of verwerp deze niet.

Als de absolute waarde van de t-teststatistiek groter is dan de kritische t-waarde, kunnen we de nulhypothese van de test verwerpen.

Anders, als de absolute waarde van de t-teststatistiek kleiner is dan de kritische t-waarde, slagen we er niet in de nulhypothese te verwerpen.

Aanvullende bronnen

Hoe leest u de verdelingstabel t
Hoe kritische waarden te vinden in Excel
Hoe kritische waarden te vinden in R