Bewerkingen op verzamelingen: vereniging, snijpunt, complement en verschil

Een set is een verzameling elementen.

We duiden een set aan met een hoofdletter en we definiëren de elementen van de set met behulp van accolades. Stel dat we bijvoorbeeld een verzameling hebben genaamd „A“ met de elementen 1, 2, 3. We zouden dit als volgt schrijven:

EEN = {1, 2, 3}

In deze tutorial worden de meest gebruikte set-bewerkingen in kansrekening en statistiek uitgelegd.

unie

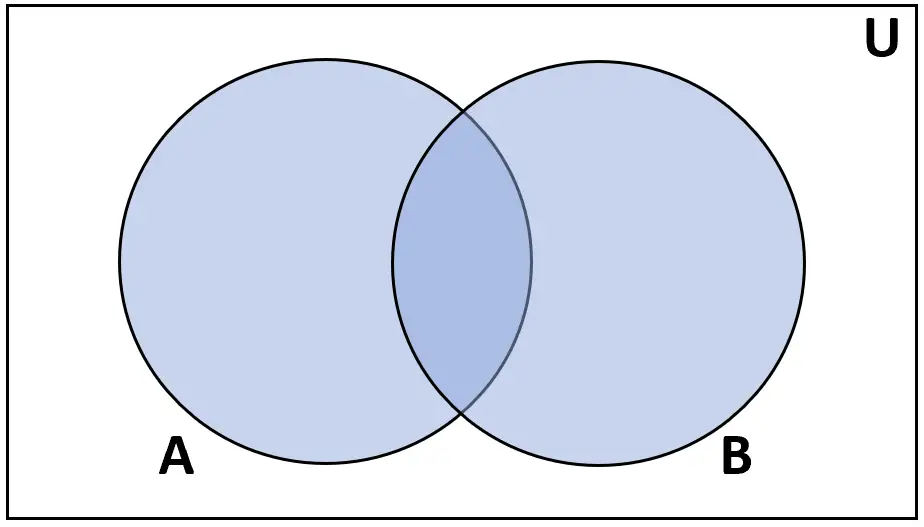
Definitie: De vereniging van verzamelingen A en B is de verzameling elementen die in A of in B voorkomen.

Beoordeling: A ∪ B

Voorbeelden:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

Kruispunt

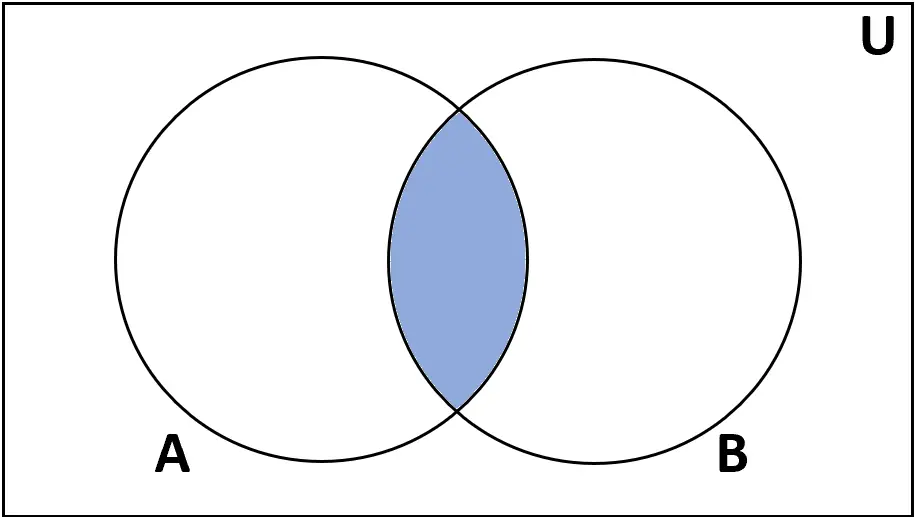
Definitie: Het snijpunt van verzamelingen A en B is de verzameling elementen die zowel in A als B voorkomen.

Notatie: A ∩ B

Voorbeelden:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

Aanvulling

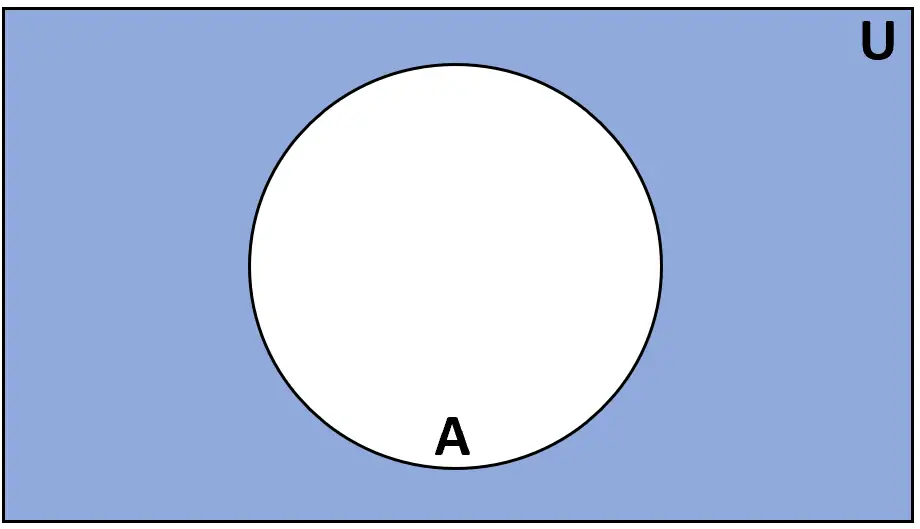
Definitie: Het complement van de verzameling A is de verzameling elementen die zich in de universele verzameling U bevinden, maar niet in A.

Beoordeling: A‘ of ^Ac

Voorbeelden:

• Als U = {1, 2, 3, 4, 5, 6} en A = {1, 2}, dan A ^c = {3, 4, 5, 6}
• Als U = {1, 2, 3} en A = {1, 2}, dan A ^c = {3}

Verschil

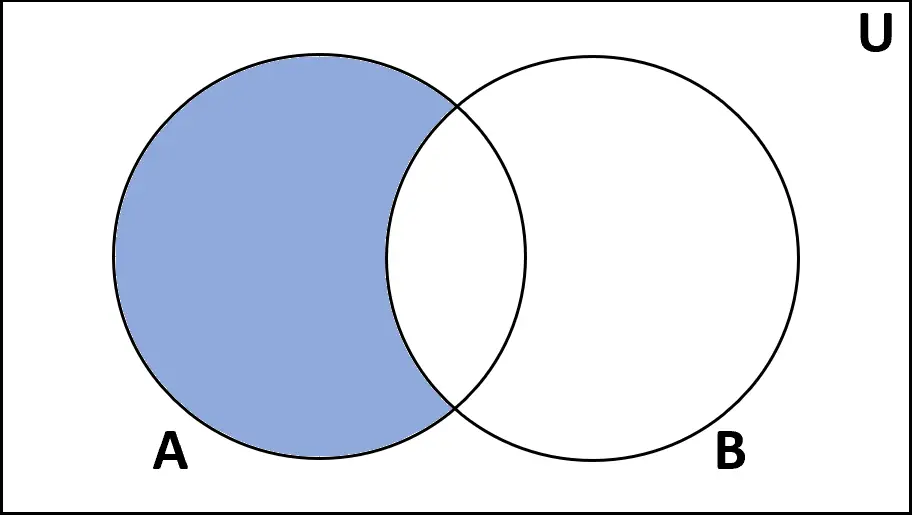
Definitie: Het verschil tussen verzamelingen A en B is de verzameling elementen die in A maar niet in B voorkomen.

Waarderingen: A – B

Voorbeelden:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

Symmetrisch verschil

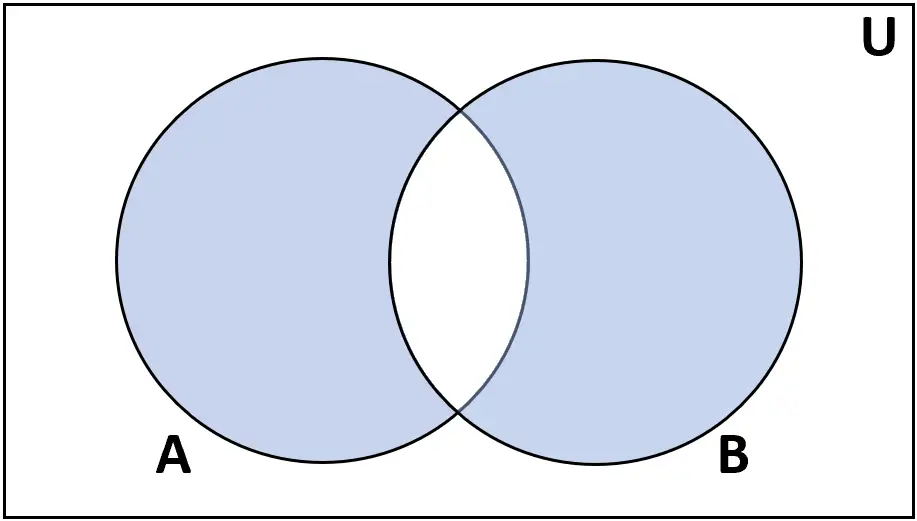
Definitie: Het symmetrische verschil tussen sets A en B is de set elementen die in A of B voorkomen, maar niet in beide.

Beoordeling: AΔB

Voorbeelden:

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

Cartesiaans product

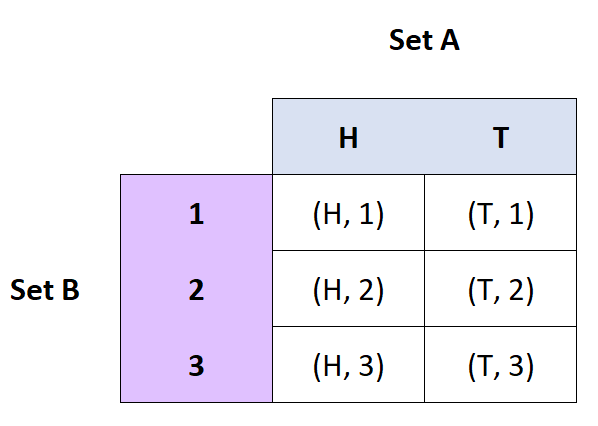
Definitie: Het cartesiaanse product van de verzamelingen A en B is de verzameling geordende paren van A en B.

Beoordeling: A x B

Voorbeelden:

• Als A = {H, T} en B = {1, 2, 3}, dan A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}
• Als A = {T, H} en B = {1, 2, 3}, dan A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}