Een inleiding tot ancova (variantieanalyse)

ANCOVA staat voor ‘analyse van covariantie’. Om te begrijpen hoe een ANCOVA werkt, helpt het om eerst ANOVA te begrijpen.

Een ANOVA   (variantieanalyse) wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Laten we bijvoorbeeld zeggen dat we willen weten of de studietechniek al dan niet van invloed is op de examenscores van een klas studenten. We verdeelden de klas willekeurig in drie groepen. Elke groep gebruikt een maand lang een andere studietechniek ter voorbereiding op een examen. Aan het einde van de maand leggen alle studenten hetzelfde examen af.

Om erachter te komen of het bestuderen van techniek invloed heeft op examenscores, kunnen we een one-way ANOVA uitvoeren, die ons vertelt of er een statistisch significant verschil is tussen de gemiddelde scores van de drie groepen.

Een ANCOVA is een uitbreiding van een ANOVA waarin we willen bepalen of er een statistisch significant verschil bestaat tussen drie of meer onafhankelijke groepen na rekening te hebben gehouden met een of meer covariabelen .

Een covariabele is een continue variabele die varieert met de responsvariabele.

Laten we bijvoorbeeld zeggen dat we willen weten of studietechniek al dan niet invloed heeft op de examenscores, maar we willen rekening houden met het cijfer dat de leerling al heeft in de klas . We kunnen hun huidige cijfer als covariabele gebruiken en een ANCOVA uitvoeren om te bepalen of er een statistisch significant verschil is tussen de gemiddelde examenscores van de drie groepen.

Hierdoor kunnen we testen of de studietechniek al dan niet invloed heeft op de examenscores zodra de invloed van de covariabele is weggenomen.

Als we dus vaststellen dat er een statistisch significant verschil is in de examenscores tussen de drie studietechnieken, kunnen we er zeker van zijn dat dit verschil bestaat , zelfs als we rekening houden met het huidige cijfer van de leerlingen in de klas (c ‚dat wil zeggen, als ze het al goed gaat of als het al goed gaat). niet in de klas) .

ANCOVA-aannames

Voordat u een ANCOVA uitvoert, is het belangrijk om ervoor te zorgen dat aan de volgende aannames wordt voldaan:

• De covariabele(n) en factorvariabele(n) zijn onafhankelijk – De covariabele en factorvariabele moeten onafhankelijk van elkaar zijn, omdat het toevoegen van een covariabele term in het model alleen zinvol is als de covariabele en de factorvariabele onafhankelijk op de responsvariabele.
• De covariaat(en) zijn continue gegevens. Covariabelen moeten continu zijn (dwz interval- of ratiogegevens).
• Homogeniteit van varianties – Varianties tussen groepen moeten ongeveer gelijk zijn.
• Onafhankelijkheid – Waarnemingen in elke groep moeten onafhankelijk zijn.
• Normaliteit – Gegevens moeten in elke groep ongeveer normaal verdeeld zijn.
• Geen extreme uitschieters – Er mogen in geen van de groepen extreme uitschieters voorkomen die de ANCOVA-resultaten aanzienlijk zouden kunnen beïnvloeden.

ANCOVA: voorbeeld

Een docent wil weten of drie verschillende studietechnieken van invloed zijn op examenscores, maar ze wil rekening houden met het huidige cijfer dat de leerling al in de klas heeft.

Er wordt een ANCOVA uitgevoerd met behulp van de volgende variabelen:

• Factorvariabele: technische studie
• Covariaat: huidige score
• Responsvariabele: examenscore

De volgende tabel presenteert de dataset van de 15 studenten die zijn gerekruteerd om aan het onderzoek deel te nemen:

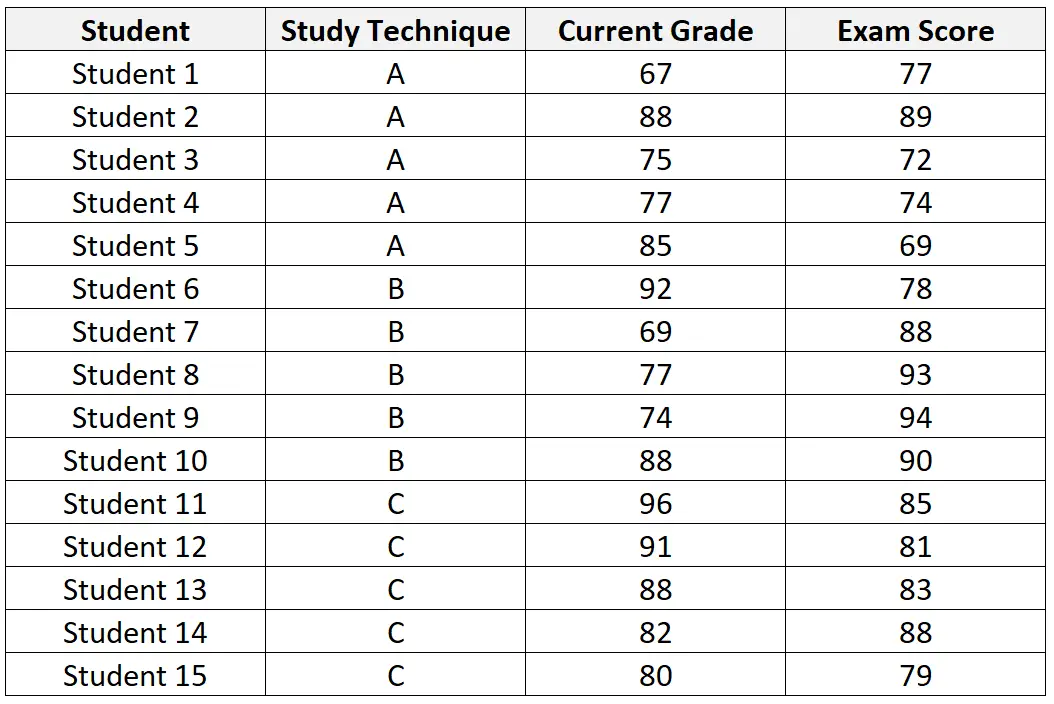
Na het uitvoeren van een ANCOVA op de dataset verkrijgt de docent de volgende resultaten:

De p-waarde voor de onderzoekstechniek is 0,03155 . Omdat deze waarde kleiner is dan 0,05, kunnen we de nulhypothese verwerpen dat elk van de studietechnieken tot hetzelfde gemiddelde examencijfer leidt, zelfs nadat rekening is gehouden met het huidige cijfer van de student in de klas .

Om precies te bepalen welke studietechnieken verschillende gemiddelde examenscores opleveren, zal de docentpost-hoc testen moeten uitvoeren.

Aanvullende bronnen

Hoe een ANCOVA uit te voeren in Excel
Hoe voer je een ANCOVA uit in R
Hoe een ANCOVA uit te voeren in Python
De verschillen tussen ANOVA, ANCOVA, MANOVA en MANCOVA