Eenrichtings-anova en herhaalde metingen-anova: het verschil

Twee soorten ANOVA-modellen waar studenten vaak tussen verward raken, zijn eenrichtings-ANOVA en eenrichtings-ANOVA met herhaalde metingen.

Hier is het simpele verschil:

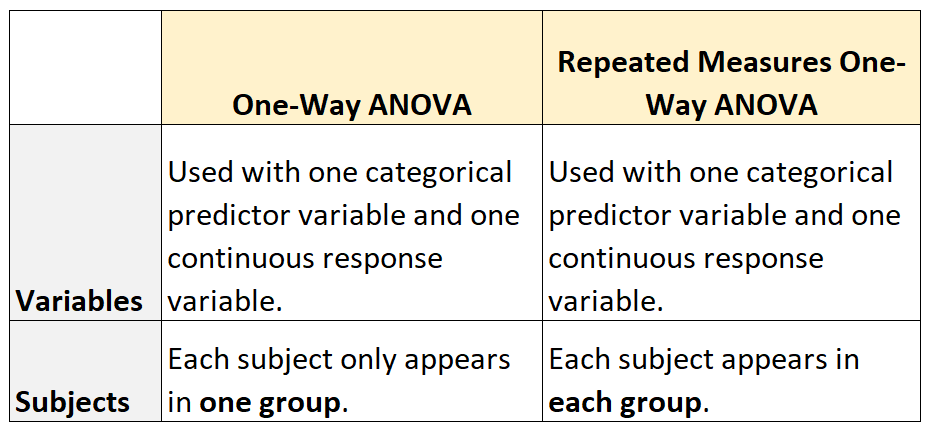
Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

Een ANOVA met herhaalde metingen in één richting wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer groepen waarin dezelfde onderwerpen in elke groep voorkomen .

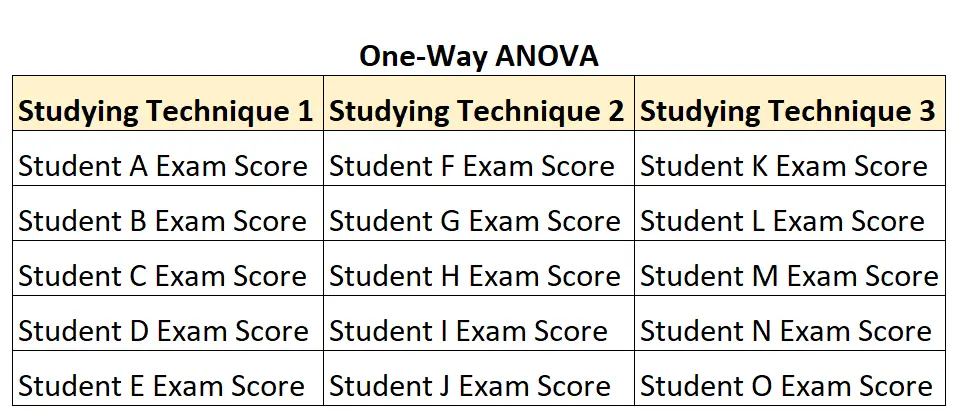
Stel bijvoorbeeld dat een hoogleraar wil vaststellen of drie verschillende studietechnieken leiden tot verschillende gemiddelde cijfers op tentamens. Om dit te testen rekruteert hij 15 studenten en wijst willekeurig 5 studenten toe om elke studietechniek een week vóór het examen te gebruiken.

Hij zou een one-way ANOVA kunnen gebruiken om te testen op verschillen tussen groepsgemiddelden, aangezien elke leerling slechts in één groep voorkomt.

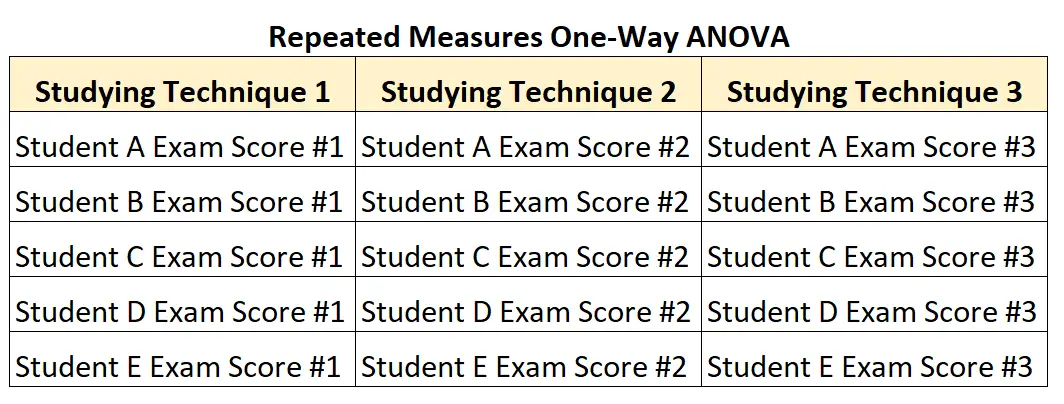
Stel echter dat de professor slechts vijf studenten rekruteert en elke student vraagt elke studietechniek drie verschillende weken te gebruiken ter voorbereiding op toetsen van gelijke moeilijkheidsgraad.

In dit scenario zou hij een ANOVA met herhaalde metingen in één richting kunnen gebruiken om te testen op verschillen tussen de gemiddelden van groepen, aangezien elke leerling in elke groep voorkomt.

Wanneer herhaalde metingen ANOVA gebruiken

Een ANOVA met herhaalde metingen wordt in twee specifieke situaties gebruikt:

1. Meet de gemiddelde scores van proefpersonen over drie of meer tijdstippen. U wilt bijvoorbeeld de rusthartslag van de proefpersonen een maand vóór aanvang van een trainingsprogramma, halverwege het programma en een maand na het programma meten om te zien of er een significant verschil is in de gemiddelde rusthartslag. door deze drie momenten.

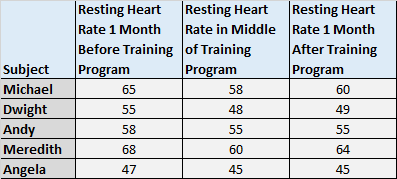
Omdat de hartslag van elke proefpersoon meerdere keren wordt gemeten, kunnen we een ANOVA met herhaalde metingen gebruiken om te bepalen of er een significant verschil is in de gemiddelde hartslag over deze drie tijdsperioden.

2. Meet de gemiddelde scores van proefpersonen in drie verschillende omstandigheden. U kunt de proefpersonen bijvoorbeeld vragen om drie verschillende films te bekijken en elke film te beoordelen op basis van hoe leuk ze deze vonden.

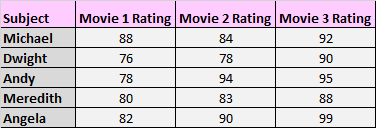
Ook hier komen in elke groep dezelfde onderwerpen voor, dus moeten we een ANOVA met herhaalde metingen gebruiken om het verschil in gemiddelden tussen deze drie condities te testen.

Voor- en nadelen van herhaalde metingen ANOVA

Een ANOVA met herhaalde metingen in één richting biedt de volgende voordelen ten opzichte van reguliere ANOVA in één richting:

1. Het is sneller en kosteneffectiever om een klein aantal individuen te rekruteren om deel te nemen aan een eenrichtings-ANOVA met herhaalde metingen, omdat onderzoekers simpelweg meerdere keren gegevens van dezelfde individuen kunnen verkrijgen.

2. Onderzoekers kunnen een deel van de variantie in de gegevens aan de individuen zelf toeschrijven, waardoor het gemakkelijker wordt om de werkelijke verschillen tussen verschillende behandelingen op te sporen.

Een ANOVA met herhaalde metingen in één richting heeft echter de volgende nadelen:

1. Als een individu het experiment verlaat, verliezen onderzoekers meer gegevens vergeleken met een reguliere eenrichtings-ANOVA.

2. Het is mogelijk dat individuen last hebben van volgorde-effecten , dat wil zeggen verschillen in het gedrag van deelnemers als gevolg van de volgorde waarin behandelingen aan hen worden gepresenteerd. Mensen kunnen bijvoorbeeld moe of moe worden tegen de tijd dat ze de laatste behandeling ondergaan.

Aanvullende bronnen

Inleiding tot One-Way ANOVA
One-way ANOVA-calculator
Inleiding tot ANOVA met herhaalde metingen
ANOVA-calculator voor herhaalde metingen in één richting