Geneste anova uitvoeren in r (stap voor stap)

Een geneste ANOVA is een type ANOVA (“variantieanalyse”) waarbij ten minste één factor binnen een andere factor is genest .

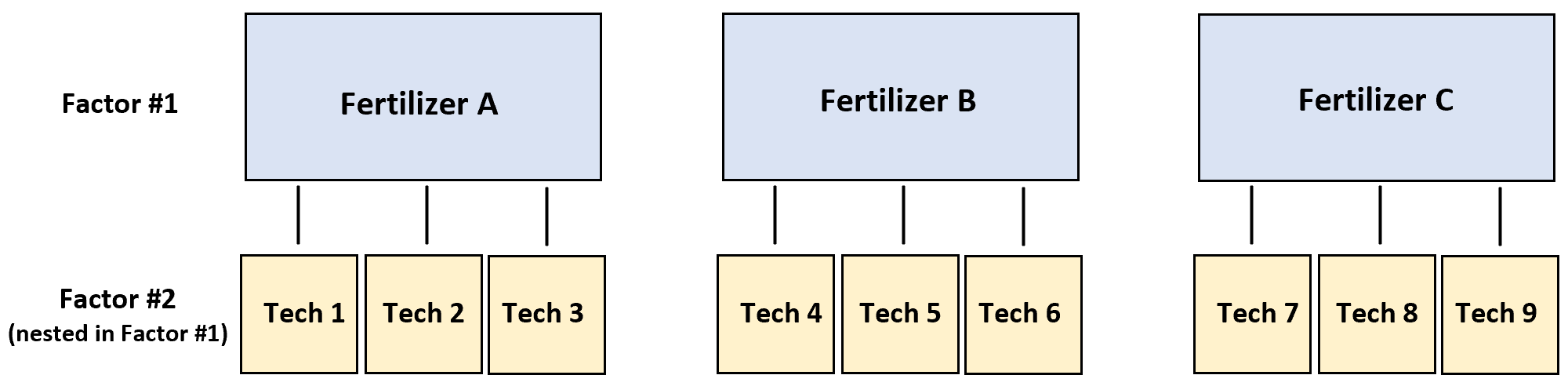
Stel dat een onderzoeker bijvoorbeeld wil weten of drie verschillende meststoffen verschillende niveaus van plantengroei opleveren.

Om dit te testen, strooien drie verschillende technici elk kunstmest A op vier planten, drie andere technici strooien elk kunstmest B op vier planten, en drie andere technici strooien elk kunstmest C op vier planten.

In dit scenario is deresponsvariabele de plantengroei en zijn de twee factoren technicus en kunstmest. Het blijkt dat de technicus zich in de kunstmest bevindt :

Het volgende stapsgewijze voorbeeld laat zien hoe u deze geneste ANOVA in R kunt uitvoeren.

Stap 1: Creëer de gegevens

Laten we eerst een dataframe maken om onze gegevens in R te bewaren:

 #create data
df <- data. frame (growth=c(13, 16, 16, 12, 15, 16, 19, 16, 15, 15, 12, 15,
                          19, 19, 20, 22, 23, 18, 16, 18, 19, 20, 21, 21,
                          21, 23, 24, 22, 25, 20, 20, 22, 24, 22, 25, 26),
                 fertilizer=c(rep(c(' A ', ' B ', ' C '), each= 12 )),
                 tech=c(rep(1:9, each= 4 )))

#view first six rows of data
head(df)

  growth fertilizer tech
1 13 A 1
2 16 A 1
3 16 A 1
4 12 A 1
5 15 A 2
6 16 A 2

Stap 2: Pas de geneste ANOVA aan

We kunnen de volgende syntaxis gebruiken om een geneste ANOVA in R te passen:

aov(antwoord ~ factor A / factor B)

Goud:

• respons: de responsvariabele
• factor A: de eerste factor
• factor B: de tweede factor genest in de eerste factor

De volgende code laat zien hoe u de geneste ANOVA voor onze dataset kunt aanpassen:

 #fit nested ANOVA
nest <- aov(df$growth ~ df$fertilizer / factor(df$tech))

#view summary of nested ANOVA
summary(nest)

                              Df Sum Sq Mean Sq F value Pr(>F)    
df$fertilizer 2 372.7 186.33 53.238 4.27e-10 ***
df$fertilizer:factor(df$tech) 6 31.8 5.31 1.516 0.211    
Residuals 27 94.5 3.50                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Stap 3: Interpreteer het resultaat

We kunnen naar de p-waardekolom kijken om te bepalen of elke factor al dan niet een statistisch significant effect heeft op de plantengroei.

Uit de bovenstaande tabel kunnen we zien dat kunstmest een statistisch significant effect heeft op de plantengroei (p-waarde < 0,05), maar technici niet (p-waarde = 0,211).

Dit vertelt ons dat als we de plantengroei willen vergroten, we ons moeten concentreren op de gebruikte meststof en niet op de individuele technicus die de meststof aanbrengt.

Stap 4: Visualiseer de resultaten

Ten slotte kunnen we boxplots gebruiken om de verdeling van de plantengroei per kunstmest en per technicus te visualiseren:

 #load ggplot2 data visualization package
library (ggplot2)

#create boxplots to visualize plant growth
ggplot(df, aes (x=factor(tech), y=growth, fill=fertilizer)) +
  geom_boxplot()

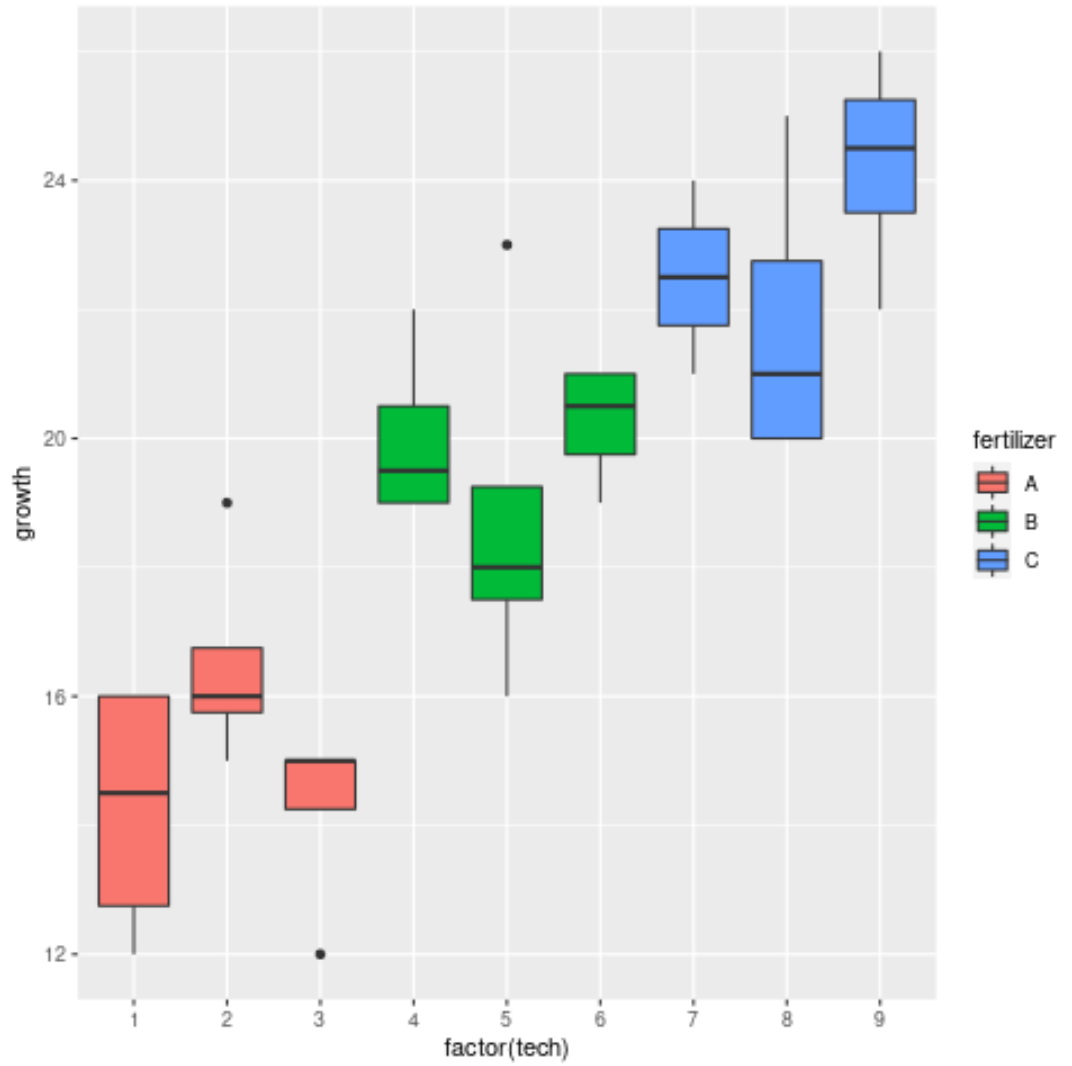
De grafiek laat zien dat er sprake is van een aanzienlijke variatie in de groei tussen de drie verschillende meststoffen, maar niet zo veel variatie tussen de technici binnen elke meststofgroep.

Dit lijkt overeen te komen met de resultaten van de geneste ANOVA en bevestigt dat meststoffen een significant effect hebben op de plantengroei, maar individuele technici niet.

Aanvullende bronnen

Eenrichtings-ANOVA uitvoeren in R
Hoe tweeweg-ANOVA uit te voeren in R
Hoe herhaalde metingen ANOVA in R uit te voeren