Anova met of zonder replicatie: wat is het verschil?

Een tweeweg-ANOVA wordt gebruikt om te bepalen of twee voorspellende variabelen (of ‘factoren’) al dan niet een statistisch significant effect hebben op een responsvariabele.

Er zijn twee verschillende typen tweeweg-ANOVA-modellen:

1. Tweerichtings-ANOVA zonder replicatie

• Voor elke combinatie van niveaus voor de voorspellende variabelen is er slechts één observatie .

2. Tweerichtings-ANOVA met replicatie

• Voor elke combinatie van niveaus voor de voorspellende variabelen zijn er meerdere waarnemingen .

Een plantkundige wil bijvoorbeeld weten of blootstelling aan de zon (Geen, Laag, Gemiddeld, Hoog) en de waterfrequentie (Dagelijks, Wekelijks) een statistisch significant effect hebben op de plantengroei.

Ze zou een van de volgende tweeweg-ANOVA-modellen kunnen uitvoeren:

1. Tweerichtings-ANOVA zonder replicatie

Met deze aanpak zou de botanicus alleen de groei van een plant meten voor elke combinatie van zonlichtniveaus en waterfrequentie.

Het mat bijvoorbeeld de groei van een plant die niet dagelijks werd blootgesteld aan zonlicht en water kreeg.

Vervolgens mat ze de groei van een enkele plant zonder blootstelling aan zonlicht en wekelijkse watergift.

Enzovoort.

De volgende tabel laat zien hoe een tweerichtings-ANOVA zonder replicatie eruit zou kunnen zien:

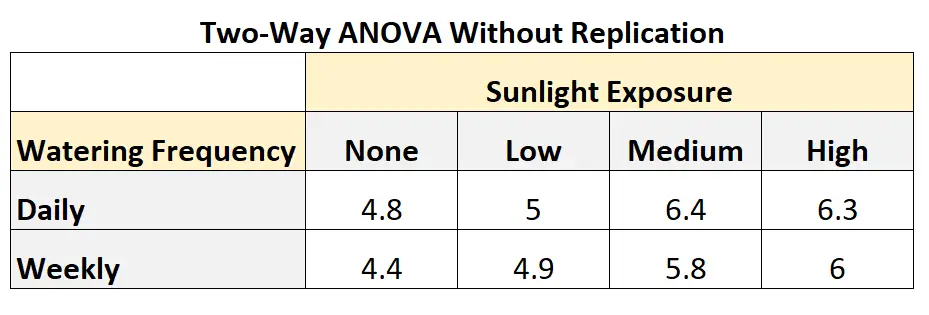
Uit de tabel kunnen we zien:

• De plant die niet werd blootgesteld aan zonlicht en dagelijks water kreeg, werd 12,5 cm lang.
• De plant zonder blootstelling aan de zon en zonder wekelijkse watergift had een groei van 10,2 cm.
• De plant met weinig blootstelling aan de zon en dagelijkse watergift groeide 5 centimeter.
• De plant met weinig blootstelling aan de zon en wekelijkse watergift groeide 11,2 cm.

Enzovoort.

2. Tweerichtings-ANOVA met replicatie

Met behulp van deze aanpak zou de botanicus de groei van meerdere planten meten voor elke combinatie van zonlichtniveaus en waterfrequentie.

Het zou bijvoorbeeld de groei kunnen meten van vijf verschillende planten die niet dagelijks worden blootgesteld aan zonlicht en water krijgen.

Vervolgens mat ze de groei van vijf andere planten zonder blootstelling aan zonlicht en zonder wekelijkse watergift.

Enzovoort.

De volgende tabel laat zien hoe een tweerichtings-ANOVA met replicatie eruit zou kunnen zien:

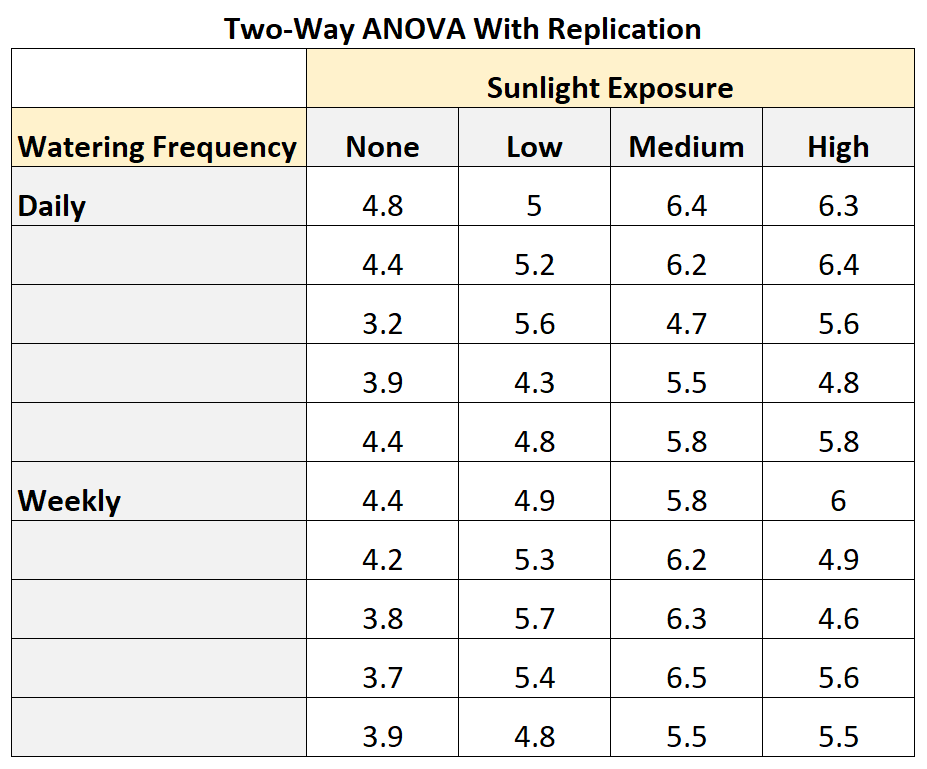
Uit de tabel kunnen we zien:

• Een plant zonder blootstelling aan de zon en dagelijkse watergift had een groei van 12,5 cm.
• Een andere plant die niet werd blootgesteld aan zonlicht en dagelijks water kreeg, werd 11,2 cm lang.
• Een andere plant die niet werd blootgesteld aan zonlicht en dagelijks water kreeg, werd 9,5 cm lang.

Enzovoort.

Het verschil tussen ANOVA met en zonder replicatie

Het grootste verschil tussen een ANOVA-model met replicatie en een ANOVA-model zonder replicatie is dat het interactie-effect tussen de twee voorspellende variabelen alleen kan worden gemeten in een ANOVA met replicatie .

Een interactie-effect betekent dat er een vorm van interactie bestaat tussen de twee voorspellende variabelen, die van invloed kan zijn op de manier waarop we de relatie tussen de voorspellende variabelen en de responsvariabele interpreteren.

De botanicus wil bijvoorbeeld misschien weten of blootstelling aan de zon en de frequentie van water geven de plantengroei beïnvloeden.

Hoewel het mogelijk is dat deze twee voorspellende variabelen de plantengroei beïnvloeden, is het ook mogelijk dat ze met elkaar interageren.

Het is bijvoorbeeld mogelijk dat blootstelling aan zonlicht ervoor zorgt dat planten met verschillende snelheden groeien, afhankelijk van of een plant dagelijks of wekelijks water krijgt.

In dit geval is er sprake van een interactie-effect tussen blootstelling aan de zon en de waterfrequentie.

De enige manier om een interactie-effect te meten is echter om meerdere metingen te hebben voor elke combinatie van niveaus voor de voorspellende variabelen.

ANOVA met en zonder replicatie in Excel

Als we een tweerichtings-ANOVA zonder replicatie in Excel uitvoeren, ziet het resultaat er als volgt uit:

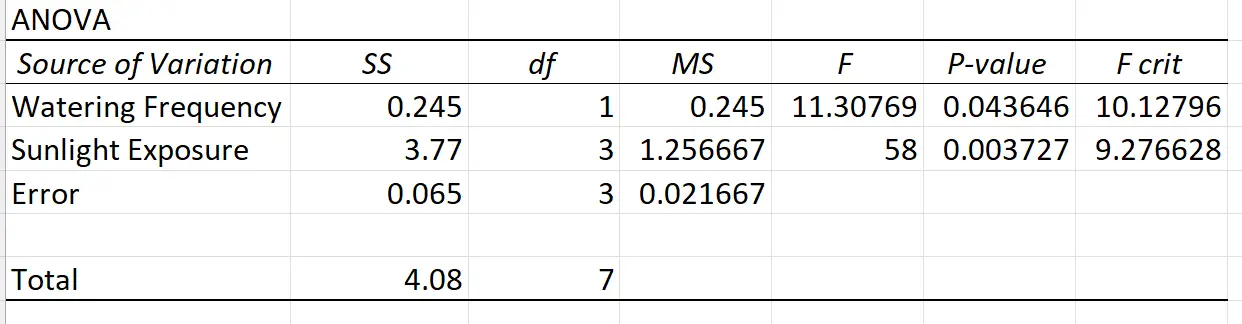
Omdat de p-waarden in de ANOVA-tabel voor blootstelling aan de zon en waterfrequentie kleiner zijn dan 0,05, zouden we kunnen concluderen dat beide variabelen een statistisch significant effect hebben op de plantengroei.

Houd er echter rekening mee dat er geen interactietermen zijn opgenomen in de ANOVA-tabel, dus we weten niet of er een interactie-effect is tussen de twee voorspellende variabelen.

Aan de andere kant, als we een tweerichtings-ANOVA met replicatie in Excel uitvoeren, ziet het resultaat er als volgt uit:

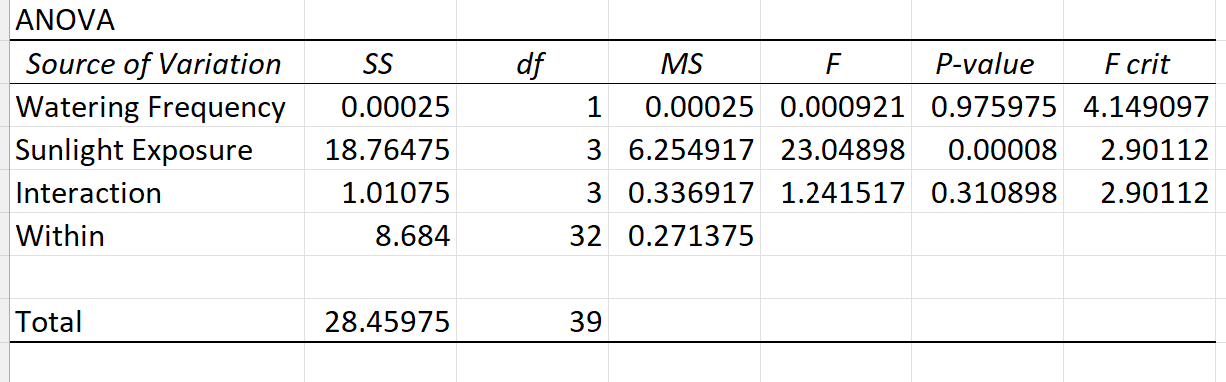
Merk op dat deze ANOVA-tabel p-waarden bevat voor blootstelling aan de zon, de waterfrequentie en het interactie-effect tussen deze twee voorspellende variabelen.

Uit de tabel kunnen we opmaken dat de waterfrequentie niet statistisch significant is, dat de blootstelling aan de zon statistisch significant is en dat er geen interactie-effect is tussen de twee voorspellende variabelen die niet statistisch significant zijn.

Dit betekent dat we conclusies kunnen trekken over de effecten van blootstelling aan de zon op de plantengroei, ongeacht de waterfrequentie .

Gerelateerd: Een tweerichtings-ANOVA uitvoeren in Excel

Aanvullende bronnen

De volgende zelfstudies bieden aanvullende informatie over tweeweg-ANOVA-modellen:

Handmatig een tweerichtings-ANOVA uitvoeren
Hoe u tweerichtings-ANOVA-resultaten rapporteert
Hoe F-waarden te interpreteren in een tweerichtings-ANOVA