Een anova uitvoeren met ongelijke steekproefgroottes

Een vraag die studenten vaak stellen als het om statistiek gaat, is:

Is het mogelijk om een one-way ANOVA uit te voeren als de steekproefomvang van elke groep niet gelijk is?

Het korte antwoord:

Ja, u kunt eenzijdige ANOVA uitvoeren als de steekproefomvang niet gelijk is. Gelijke steekproefgroottes behoren niet tot de aannames in een ANOVA.

Er zijn echter twee mogelijke problemen waarmee u rekening moet houden bij het uitvoeren van een eenrichtings-ANOVA met ongelijke steekproefomvang:

(1) Verminderde statistische kracht.

(2) Robuustheid gereduceerd tot ongelijke variantie.

In de volgende paragrafen worden deze twee potentiële problemen gedetailleerd uitgelegd.

Probleem #1: Verminderde statistische kracht

Wanneer we welk type statistische test dan ook gebruiken om groepen te vergelijken, is de statistische kracht van de test het hoogst wanneer elke groep een gelijke steekproefomvang heeft.

Bedenk dat statistische power verwijst naar de waarschijnlijkheid dat een test een effect detecteert terwijl er daadwerkelijk een effect bestaat.

Er kan worden aangetoond dat hoe groter de verschillen in de steekproefomvang tussen groepen zijn, hoe lager de statistische kracht van een ANOVA.

Dit is de reden waarom onderzoekers over het algemeen gelijke steekproefgroottes willen om een grotere power te hebben en daardoor een grotere kans om echte verschillen te ontdekken.

Het is zeker mogelijk om een eenrichtings-ANOVA uit te voeren met ongelijke steekproefgroottes, maar u moet er rekening mee houden dat de kracht van de eenrichtings-ANOVA kleiner zal zijn.

Probleem #2: Robuustheid gereduceerd tot ongelijke variantie

Een van de aannames van een eenrichtings-ANOVA is dat de variantie tussen elke groep gelijk is.

Over het algemeen wordt een eenrichtings-ANOVA als robuust beschouwd voor schendingen van de aanname van gelijke varianties, maar alleen als elke groep dezelfde steekproefomvang heeft .

Als u dus ongelijke steekproefgroottes en ongelijke varianties tussen groepen heeft, kunnen de resultaten van eenrichtings-ANOVA moeilijk te vertrouwen zijn.

Hoe u kunt beslissen of u een eenrichtings-ANOVA wilt gebruiken bij ongelijke steekproefgroottes

Als u ongelijke steekproefgroottes heeft en een eenrichtings-ANOVA wilt uitvoeren om te testen op verschillen tussen groepsgemiddelden, kunt u het volgende stroomdiagram gebruiken om te beslissen hoe u verder moet gaan:

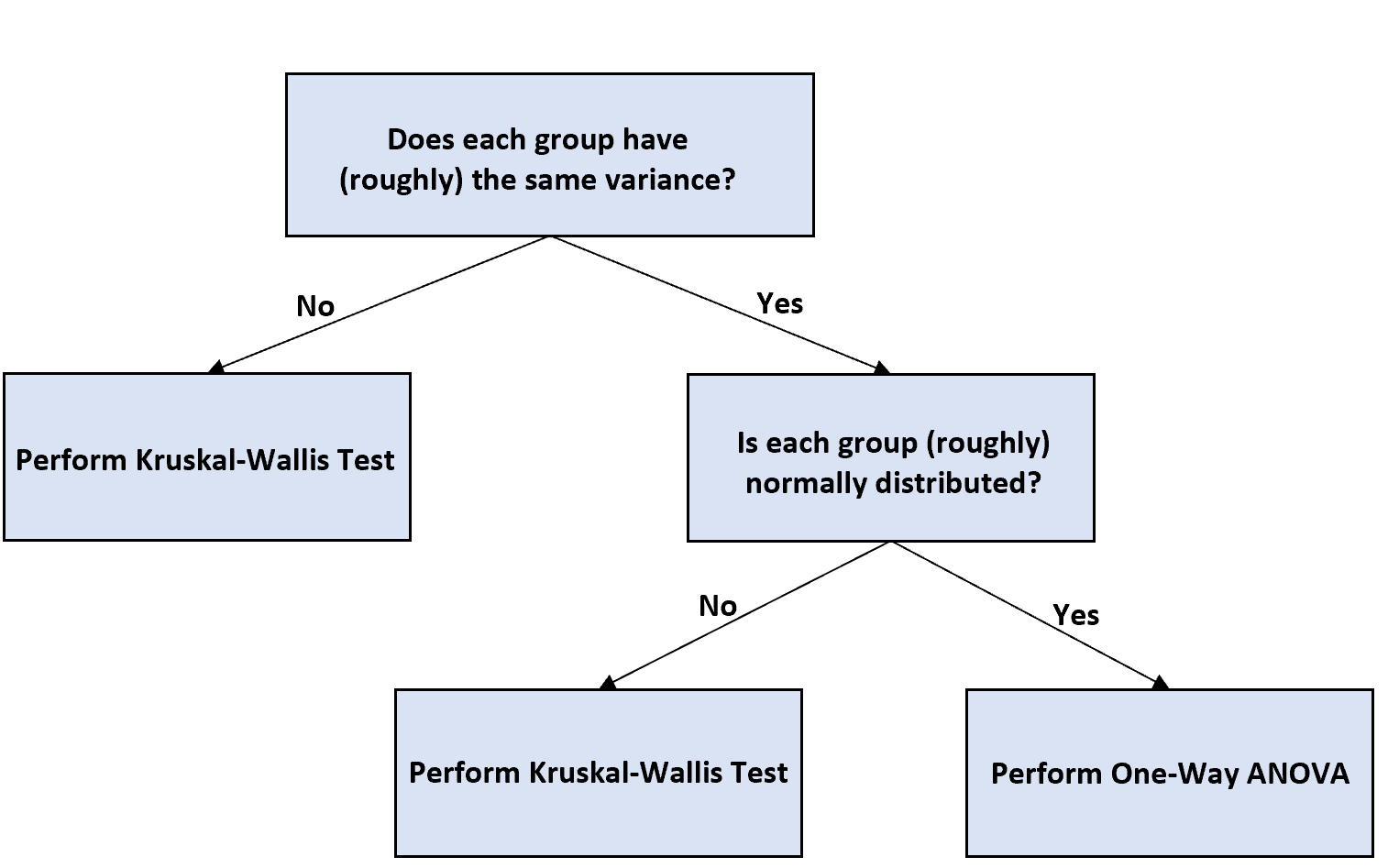
Hier volgt een korte uitleg van het stroomschema:

Stap 1: Bepaal of elke groep dezelfde variantie heeft.

Om te bepalen of elke groep dezelfde variantie heeft, kunt u een van de volgende twee benaderingen gebruiken:

• Maak boxplots voor elke groep en kijk of de verdeling van waarden in elke groep ongeveer gelijk is.
• Voer een formele statistische test uit voor gelijke varianties, zoals de Bartlett-test .

Als de varianties niet gelijk zijn, voert u een Kruskal-Wallis-test uit, die wordt beschouwd als het niet-parametrische equivalent van een eenrichtings-ANOVA.

Als de gaten gelijk zijn, gaat u verder met de volgende stap.

Stap 2: Bepaal of elke groep normaal verdeeld is.

Om te bepalen of de waarden in elke groep ongeveer normaal verdeeld zijn, kunt u een van de volgende twee benaderingen gebruiken:

• Maak histogrammen ofQQ-plots voor elke groep.
• Voer formele statistische tests uit zoals Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre of D’Agostino-Pearson.

Als elke groep normaal verdeeld is, kunt u een eenrichtings-ANOVA uitvoeren en de resultaten interpreteren zoals u dat bij elke gewone eenrichtings-ANOVA zou doen.

Als elke groep niet normaal verdeeld is, voer dan een Kruskal-Wallis-test uit.

Aanvullende bronnen

Een inleiding tot One-Way ANOVA
Hoe u ANOVA-aannames kunt controleren
Een inleiding tot de Kruskal-Wallis-test
Hoe F-waarde en P-waarde in ANOVA te interpreteren