Eenrichtings-anova uitvoeren op een ti-84-rekenmachine

Een eenrichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen.

In deze tutorial wordt uitgelegd hoe u een one-way ANOVA uitvoert op een TI-84-rekenmachine.

Voorbeeld: One-way ANOVA op een TI-84-rekenmachine

Stel dat we 30 studenten werven voor deelname aan een onderzoek. Studenten worden willekeurig toegewezen om een maand lang een van de drie studietechnieken te gebruiken ter voorbereiding op een examen. Aan het einde van de maand maken alle studenten dezelfde toets.

Gebruik de volgende stappen om een eenrichtings-ANOVA uit te voeren om te bepalen of de gemiddelde scores voor de drie groepen hetzelfde zijn.

Stap 1: Voer de gegevens in.

Eerst voeren we de gegevenswaarden in voor de verklarende variabele en de responsvariabele. Druk op Stat en vervolgens op BEWERKEN . Vul de volgende examenresultaten in voor studenten die de eerste studietechniek in kolom L1, de tweede studietechniek in kolom L2 en de derde studietechniek in kolom L3 gebruikten:

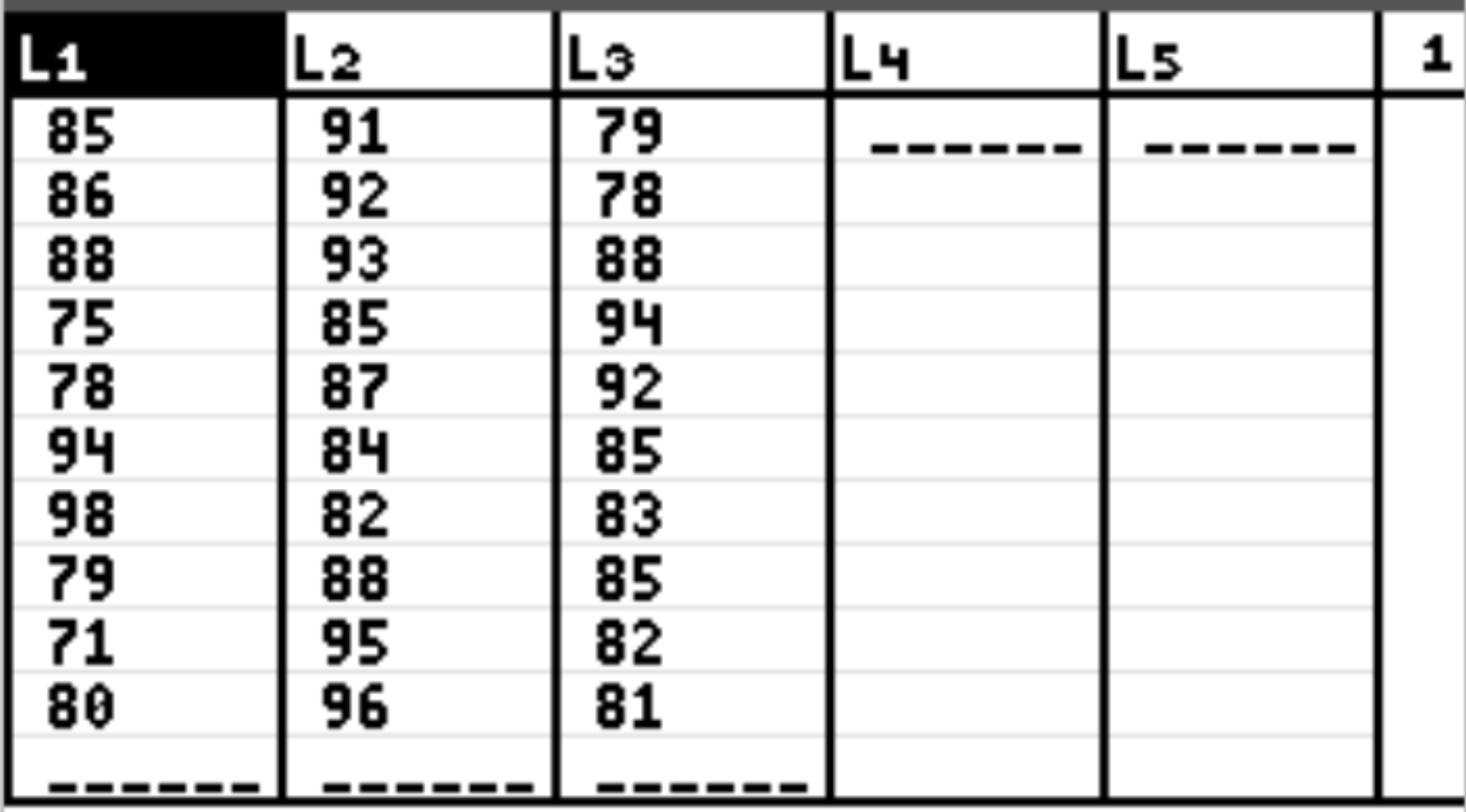
Stap 2: Voer eenrichtings-ANOVA uit.

Vervolgens voeren we de one-way ANOVA uit. Druk op Stat en scroll vervolgens naar TESTS . Blader vervolgens omlaag naar ANOVA en druk op Enter .

Voer de lijsten in waar de gegevens zijn opgeslagen, gescheiden door komma’s, voeg vervolgens een haakje sluiten toe en druk op Enter .

Opmerking: Om L1 weer te geven, drukt u op 2 en vervolgens op 1 . Om L2 weer te geven, drukt u op 2nd en vervolgens op 2 . Om L3 weer te geven, drukt u op 2nd en vervolgens op 3 .

De volgende resultaten verschijnen zodra u op Enter drukt:

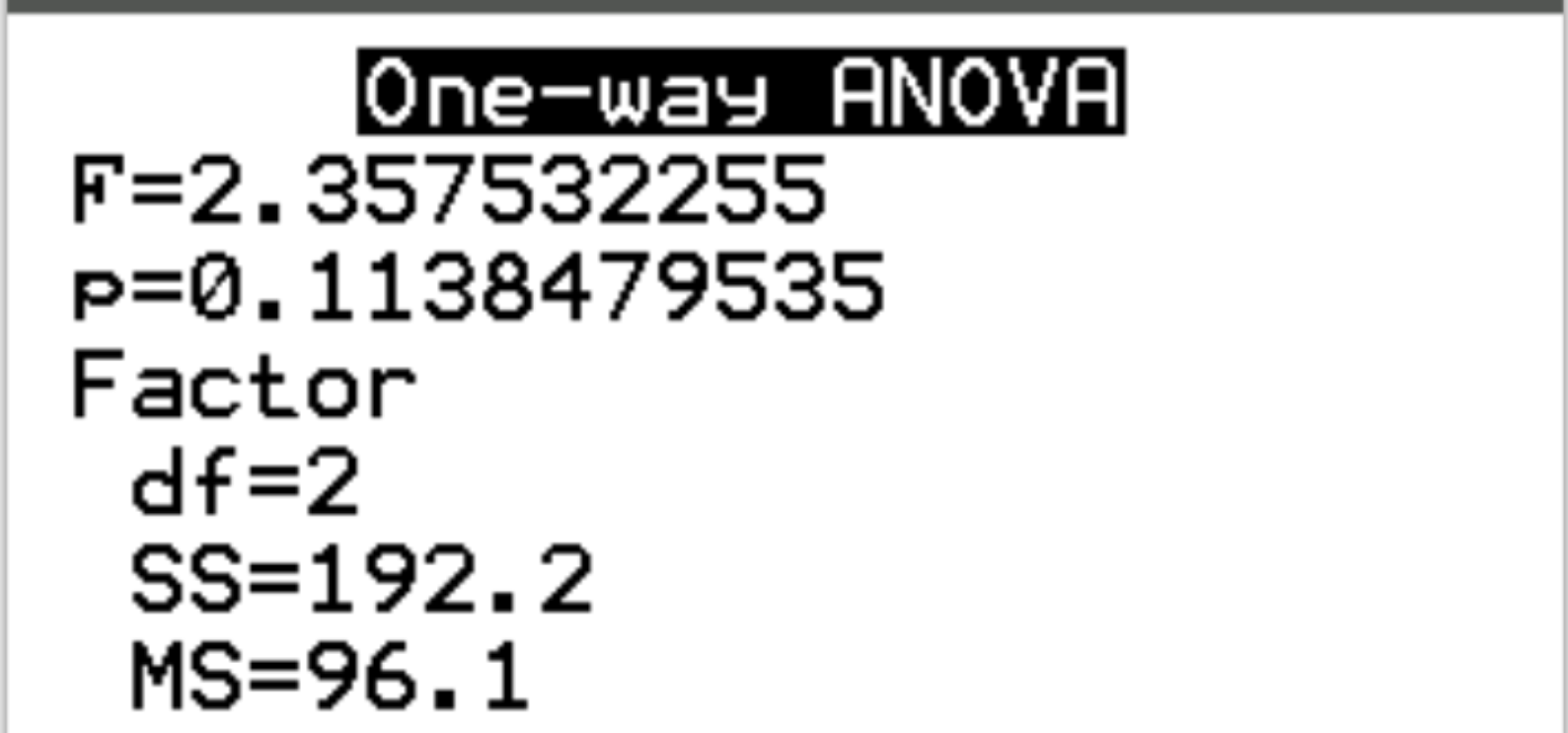
Stap 3: Interpreteer de resultaten.

De F-statistiek van de test is 2,3575 en de overeenkomstige p-waarde is 0,1138 . Omdat deze p-waarde niet kleiner is dan 0,05, slagen we er niet in de nulhypothese te verwerpen.

Daarom hebben we onvoldoende bewijs om te zeggen dat de gemiddelde examenscore tussen de drie groepen verschillend is. Met andere woorden: we hebben niet genoeg bewijs om te zeggen dat de onderzoekstechniek tot verschillende testresultaten leidt.