Hoe scheefheid en kurtosis in r te berekenen

In de statistiek zijn scheefheid en kurtosis twee manieren om de vorm van een verdeling te meten.

Scheefheid is een maatstaf voor de scheefheid van een verdeling. Deze waarde kan positief of negatief zijn.

• Negatieve scheefheid geeft aan dat de staart zich aan de linkerkant van de verdeling bevindt, die zich uitstrekt naar meer negatieve waarden.
• Een positieve scheefheid geeft aan dat de staart zich aan de rechterkant van de verdeling bevindt, die zich uitstrekt naar meer positieve waarden.
• Een waarde nul geeft aan dat er geen asymmetrie in de verdeling is, wat betekent dat de verdeling perfect symmetrisch is.

Kurtosis is een maatstaf voor de vraag of een verdeling zwaar of lichtstaartig is vergeleken met eennormale verdeling .

• De kurtosis van een normale verdeling is 3.
• Als een bepaalde verdeling een kurtosis van minder dan 3 heeft, wordt er gesproken van playkurtic , wat betekent dat deze de neiging heeft om minder en minder extreme uitschieters te produceren dan de normale verdeling.
• Als een bepaalde verdeling een kurtosis groter dan 3 heeft, wordt er gezegd dat deze leptokurtisch is, wat betekent dat deze de neiging heeft om meer uitschieters te produceren dan de normale verdeling.

Opmerking: Sommige formules (Fisher-definitie) trekken 3 af van de kurtosis om vergelijking met de normale verdeling te vergemakkelijken. Met behulp van deze definitie zou een verdeling een grotere kurtosis hebben dan een normale verdeling als deze een kurtosis-waarde groter dan 0 had.

In deze tutorial wordt uitgelegd hoe u zowel scheefheid als kurtosis van een bepaalde dataset in R kunt berekenen.

Voorbeeld: scheefheid en afvlakking in R

Stel dat we de volgende dataset hebben:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

We kunnen de verdeling van waarden in deze dataset snel visualiseren door een histogram te maken:

 hist(data, col=' steelblue ') 

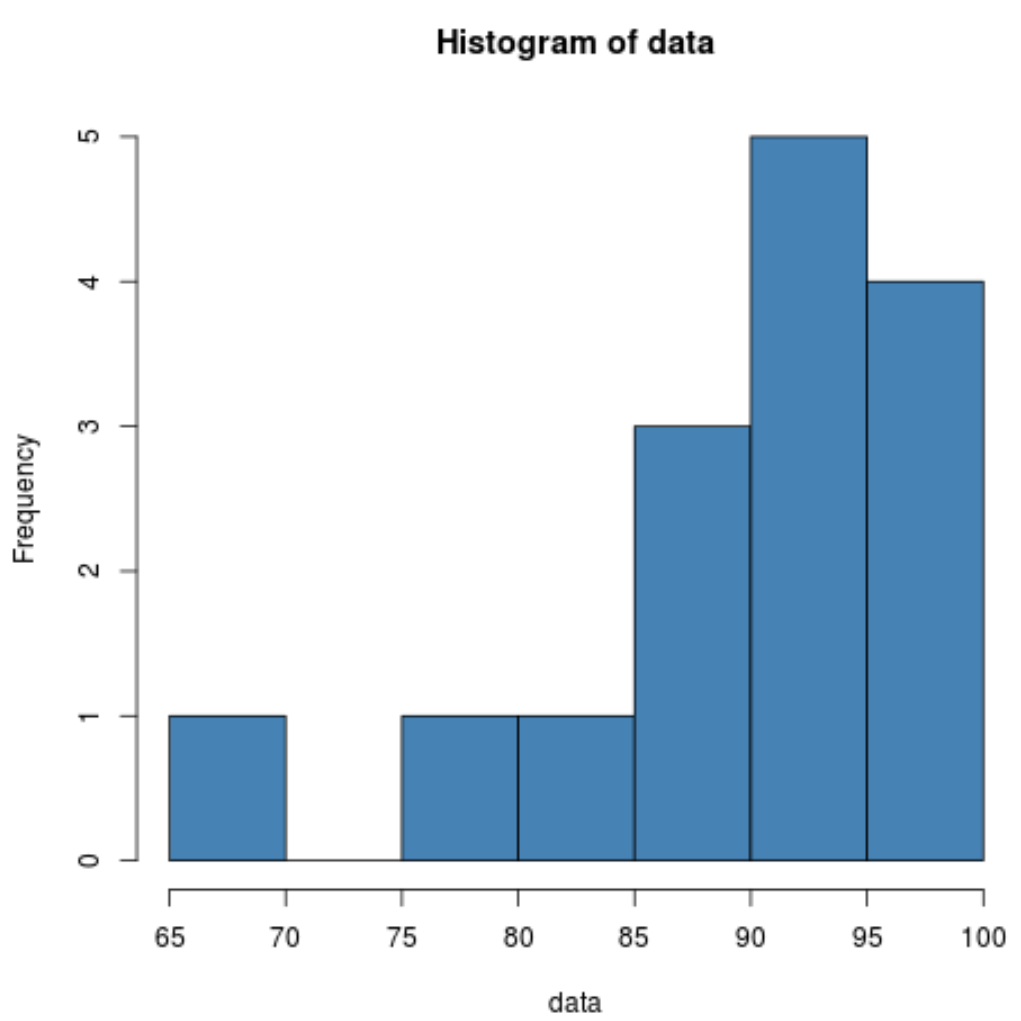
Uit het histogram blijkt dat de verdeling naar links scheef lijkt te zijn. Dat wil zeggen dat een groter deel van de waarden geconcentreerd is aan de rechterkant van de verdeling.

Om de scheefheid en kurtosis van deze dataset te berekenen, kunnen we de functies skewness() en kurtosis() gebruiken vanaf de momentbibliotheek in R:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

De scheefheid blijkt -1.391777 te zijn en de kurtosis blijkt 4.177865 te zijn.

Omdat de scheefheid negatief is, duidt dit erop dat de verdeling scheef blijft. Dit bevestigt wat we in het histogram zagen.

Omdat de kurtosis groter is dan 3, geeft dit aan dat de verdeling meer waarden in de staarten heeft vergeleken met een normale verdeling.

De momentenbibliotheek biedt ook de functie jarque.test() , die een goodness-of-fit-test uitvoert die bepaalt of de voorbeeldgegevens al dan niet scheefheid en kurtosis vertonen die consistent zijn met een normale verdeling. De nul- en alternatieve hypothesen van deze test zijn als volgt:

Nulhypothese : de dataset vertoont scheefheid en kurtosis die overeenkomt met een normale verdeling.

Alternatieve hypothese : de dataset vertoont scheefheid en kurtosis die niet overeenkomt met een normale verdeling.

De volgende code laat zien hoe u deze test uitvoert:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

De p-waarde van de test blijkt 0,05756 te zijn. Omdat deze waarde niet kleiner is dan α = 0,05, slagen we er niet in de nulhypothese te verwerpen. We hebben niet voldoende bewijs om te zeggen dat deze dataset een scheefheid en kurtosis heeft die verschilt van de normale verdeling.

De volledige documentatie van de Moments Library vindt u hier .

Bonus: scheefheids- en kurtosis-calculator

U kunt de scheefheid voor een bepaalde gegevensset ook berekenen met behulp van de Statistical Skewness and Kurtosis Calculator , die automatisch de scheefheid en kurtosis voor een bepaalde gegevensset berekent.