De stelling van bayes

Von August 1, 2023 Waarschijnlijkheid Keine Kommentare

Dit artikel legt uit wat de stelling van Bayes is en waarvoor het wordt gebruikt in kansrekening en statistiek. Zo ontdek je wat de formule is van de stelling van Bayes, opgeloste voorbeelden van de stelling van Bayes en wat de toepassingen van deze stelling zijn.

Wat is de stelling van Bayes?

In de waarschijnlijkheidstheorie is de stelling van Bayes een wet die wordt gebruikt om de waarschijnlijkheid van een gebeurtenis te berekenen wanneer a priori informatie over die gebeurtenis bekend is.

Meer specifiek relateert de stelling van Bayes op wiskundige wijze de waarschijnlijkheid van gebeurtenis A gegeven gebeurtenis B aan de waarschijnlijkheid van B gegeven A.

Als u bijvoorbeeld van tevoren weet hoe waarschijnlijk het is dat iemand hoofdpijn krijgt als hij griep heeft, kunt u de stelling van Bayes gebruiken om de waarschijnlijkheid te bepalen dat iemand griep krijgt als hij hoofdpijn heeft.

De stelling van Bayes kent vele toepassingen. Het wordt bijvoorbeeld gebruikt in de geneeskunde, de economie of de technologie om de waarschijnlijkheid van bepaalde gebeurtenissen te berekenen, afhankelijk van andere gebeurtenissen. Hieronder zullen we in detail ingaan op de verschillende toepassingen van de stelling van Bayes.

De stelling van Bayes werd uitgevonden door de Engelse wiskundige Thomas Bayes (1702-1761), hoewel deze postuum in 1763 werd gepubliceerd.

Formule van de stelling van Bayes

De stelling van Bayes zegt dat gegeven een voorbeeldruimte die is samengesteld uit een reeks elkaar uitsluitende gebeurtenissen {A 1 , A 2 ,…, A i ,…, A n } waarvan de kansen niet nul zijn en een andere gebeurtenis B , we de voorwaardelijke gebeurtenis wiskundig kunnen relateren waarschijnlijkheid van A i gegeven de gebeurtenis B met de voorwaardelijke waarschijnlijkheid van B gegeven A i .

De formule voor de stelling van Bayes , ook bekend als de regel van Bayes , is dus:

Formule van de stelling van Bayes, de regel van Bayes

Goud:

  • P(A_i|B)

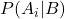
    is de voorwaardelijke waarschijnlijkheid van gebeurtenis A i gegeven gebeurtenis B, de posterieure waarschijnlijkheid genoemd.

  • P(B|A_i)

    is de voorwaardelijke waarschijnlijkheid van gebeurtenis B gegeven gebeurtenis Ai .

  • P(A_i)

    is de waarschijnlijkheid dat gebeurtenis A i zal plaatsvinden, de a priori waarschijnlijkheid genoemd.

Merk op dat de noemer van de stellingformule van Bayes de totale waarschijnlijkheid van gebeurtenis B is.

Voorbeeld van de stelling van Bayes

Zodra we de definitie van de stelling van Bayes zien en wat de formule ervan is, zullen we een opgelost voorbeeld zien van hoe een waarschijnlijkheid wordt berekend met de stelling van Bayes om het concept beter te begrijpen.

  • Een elektronicawinkel verkoopt televisies van drie merken: X, Y, Z. Er wordt geschat dat 20% van de omzet bestaat uit televisies van het merk die defect zijn, 3% van de televisies van het merk Y zijn defect en 4% van de televisies van het merk Z zijn defect. Hoe groot is de kans dat het een merk Z-tv betreft, gegeven een defecte tv?

De oefening geeft ons de kansen dat een klant elk televisiemerk zal kopen:

  • Gebeurtenis A 1 : Een klant koopt een televisie van merk X → P(A 1 )=0,20
  • Gebeurtenis A 2 : Een klant koopt een televisie van het merk Y → P(A 2 )=0,50
  • Gebeurtenis A 3 : Een klant koopt een televisie van het merk Z → P(A 3 )=0,30

Daarnaast geeft de meting ons ook de kans dat een televisie van elk merk defect is:

Gebeurtenis B: De tv is defect

  • B|A 1 : Bij een televisie van merk X is de televisie defect → P(B|A 1 )=0,05
  • B|A 2 : Bij een televisie van merk Y is de televisie defect → P(B|A 2 )=0,03
  • B|A 3 : Bij een merk Z televisie is de televisie defect → P(B|A 3 )=0,04

Dus de waarschijnlijkheidsboom van alle gebeurtenissen die ons interesseren is als volgt:

Boomdiagram van de stelling van Bayes

Om dus de waarschijnlijkheid te berekenen dat het bij een defecte televisie om merk Z gaat, moeten we de formule uit de stelling van Bayes gebruiken:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

Met behulp van de terminologie die in dit voorbeeld wordt gebruikt, ziet de formule van Bayes er als volgt uit:

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

De berekening van de waarschijnlijkheid dat een bepaalde defecte televisie van merk Z is, is dus als volgt:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}

Concluderend is de kans dat als een televisie defect is, het merk Z is, 32%.

Toepassingen van de stelling van Bayes

Er zijn veel toepassingen van de stelling van Bayes, waaronder:

  1. Medische tests : De stelling van Bayes wordt in de geneeskunde vaak gebruikt om de waarschijnlijkheid te bepalen dat diagnostische tests worden doorstaan. In het geval van een HIV-test kan de stelling bijvoorbeeld worden gebruikt om de kans te berekenen dat iemand het virus daadwerkelijk heeft als de testuitslag positief is.
  2. Financiële analyse : In de financiële wereld wordt de stelling van Bayes gebruikt om de waarschijnlijkheid te berekenen dat bepaalde economische gebeurtenissen, zoals een stijging of daling van de aandelenwaarde, zullen plaatsvinden gegeven een reeks economische variabelen.
  3. Marktonderzoek : De stelling van Bayes maakt het mogelijk om bijvoorbeeld de waarschijnlijkheid te bepalen dat iemand een product zal kopen nadat hij een advertentie voor dit product heeft gezien.
  4. Weersvoorspellingen : Weermodellen gebruiken ook de stelling van Bayes om de waarschijnlijkheid te bepalen dat een bepaalde weersvoorspelling op basis van waargenomen gegevens uitkomt. Dit verbetert de nauwkeurigheid van klimaatvoorspellingen.
  5. Computerbeveiliging – Op het gebied van cyberbeveiliging kan de stelling van Bayes worden toegepast om de waarschijnlijkheid te bepalen dat een verdachte activiteit werkelijk een aanval op het computersysteem is.

Problemen met de stelling van Bayes opgelost

Oefening 1

Er wordt geschat dat 1% van de bevolking aan een ziekte lijdt. Een test om deze ziekte op te sporen is 95% nauwkeurig voor positieve gevallen en 90% nauwkeurig voor negatieve gevallen. Als een willekeurig geselecteerde persoon positief test, wat is dan de kans dat hij/zij de ziekte daadwerkelijk heeft?

De oefenverklaring geeft ons de volgende kansen:

A 1 : De persoon heeft de ziekte → P(A 1 )=0,01
A 2 : De persoon heeft de ziekte niet → P(A 2 )=0,99

B: De test is positief
B|A 1 : De test is positief als de persoon de ziekte heeft → P(B|A 1 )=0,95
B|A 2 : De test is positief als de persoon de ziekte niet heeft → P(B|A 2 )=1-0,90=0,10

Om vervolgens de waarschijnlijkheid te berekenen dat een willekeurig geselecteerde persoon de ziekte daadwerkelijk heeft wanneer hij positief wordt getest, moet de regel van Bayes worden toegepast:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_1|B)=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}

Dus vervangen we de waarden in de formule en voeren de waarschijnlijkheidsberekening uit:

\begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}

Kortom, de kans dat een willekeurig gekozen persoon positief test en daadwerkelijk de ziekte heeft, is 8,76%.

Oefening 2

Er wordt geschat dat de kans dat een aandeel op één dag zal stijgen 40% is, dat het stabiel zal blijven 10% en dat het zal dalen 50%. Bovendien weten we dat wanneer de markt stijgt, er een kans van 90% is dat een financieel analist dit correct zal voorspellen, dat wanneer de markt stabiel blijft, de kans dat de voorspelling correct zal zijn 75% is en dat in geval van een daling, de kans op een juiste voorspelling is 75%. 85%.%. Als een analist voorspelt dat de markt zal dalen, hoe waarschijnlijk is het dan dat deze daadwerkelijk zal dalen?

In dit geval biedt de oefenverklaring ons de volgende kansen:

A 1 : De markt stijgt in één dag → P(A 1 )=0,40
A 2 : De markt blijft stabiel gedurende één dag → P(A 2 )=0,10
A 3 : De markt stijgt in één dag → P(A 3 )=0,50

B: De analist voorspelt dat de markt zal dalen
B|A 1 : De analist voorspelt correct dat de markt zal stijgen → P(B|A 1 )=0,90
B|A 2 : De analist voorspelt correct dat de markt stabiel blijft → P(B|A 2 )=0,75
B|A 3 : De analist voorspelt correct dat de markt zal dalen → P(B|A 3 )=0,85

Om de waarschijnlijkheid te bepalen dat een analist een voorspelling doet dat de markt zal dalen en dat deze juist is, moeten we de formule van de stelling van Bayes gebruiken:

P(A_i|B)=\cfrac{P(B|A_i)\cdot P(A_i)}{\displaystyle \sum_{k=1}^n P(B|A_k)\cdot P(A_k)}

P(A_3|B)=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}

We vervangen de waarschijnlijkheidswaarden in de formule van Bayes en berekenen de waarschijnlijkheid:

\begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}

Daarom is de kans dat een analist gelijk heeft als hij zegt dat de aandelenmarkt zal dalen 49,42%.

Über den Autor

Dr.benjamin anderson
Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Einen Kommentar hinzufügen

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert