Waarom is de mediaan belangrijk in statistieken?

De mediaan vertegenwoordigt de middelste waarde van een dataset, wanneer alle waarden zijn gerangschikt van klein naar groot.

De mediaan in de volgende gegevensset is bijvoorbeeld 19:

Gegevensset: 3, 4, 11, 15, 19 , 22, 23, 23, 26

De mediaan vertegenwoordigt ook het ^50e percentiel van een dataset. Dat wil zeggen dat precies de helft van de waarden in de dataset boven de mediaan ligt en de helft van de waarden eronder.

De mediaan is een belangrijke maatstaf om te berekenen, omdat deze ons een idee geeft van waar het ‘centrum’ van een dataset zich bevindt. Dit geeft ons ook een idee van de “typische” waarde in een bepaalde dataset.

Laten we bijvoorbeeld zeggen dat we een dataset hebben met de verkoopprijzen van 10.000 verschillende huizen in een bepaalde stad.

In plaats van naar rijen en rijen ruwe gegevens te kijken, kunnen we de mediaanwaarde berekenen om snel inzicht te krijgen in de gemiddelde verkoopprijs van woningen in die stad.

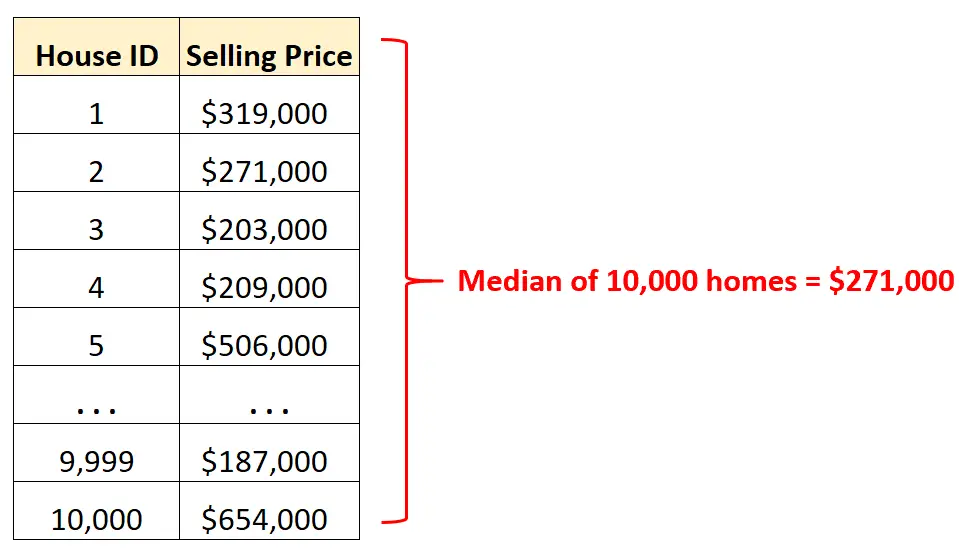
Wetende dat de gemiddelde verkoopprijs $271.000 bedraagt, weten we dat precies de helft van de 10.000 woningen voor meer dan dat bedrag is verkocht en de andere helft voor minder.

Dit geeft ons ook een idee van de ‘typische’ verkoopprijs van woningen in deze stad.

Wanneer moet u de mediaan gebruiken?

Bij het analyseren van datasets willen we vaak begrijpen waar de centrale waarde ligt.

In de statistiek zijn er twee veelgebruikte maatstaven die we gebruiken om het middelpunt van een dataset te meten:

• Gemiddelde : de gemiddelde waarde in een reeks gegevens
• Mediaan : de mediaanwaarde in een gegevensset

Het blijkt dat de mediaan een nuttiger maatstaf is in de volgende omstandigheden:

• Wanneer de verdelingasymmetrisch is.
• Wanneer de verdeling uitschieters bevat.

Om dit te illustreren, bekijken we de volgende twee voorbeelden.

Voorbeeld 1: Berekening van de mediaan van een scheve verdeling

Beschouw de volgende loonverdeling voor inwoners van een bepaalde stad:

De mediaan weerspiegelt het “typische” salaris van een inwoner beter dan het gemiddelde, omdat de verdeling scheef naar rechts is.

Dit betekent dat hoge lonen aan de rechterkant van de verdeling het gemiddelde wegduwen van het centrum van de verdeling.

In dit specifieke voorbeeld is het gemiddelde salaris $47.000, terwijl het gemiddelde salaris $32.000 is. De mediaan is veel representatiever voor het typische salaris in deze stad.

Voorbeeld 2: Berekening van de mediaan bij aanwezigheid van uitbijters

Bekijk de volgende grafiek die het aantal vierkante meters huizen in een bepaalde straat laat zien:

Het gemiddelde wordt sterk beïnvloed door enkele extreem grote huizen, terwijl de mediaan dat niet is.

We kunnen zien dat de mediaan de ‘typische’ vierkante meters van een huis in die straat beter weergeeft dan het gemiddelde, omdat deze niet wordt beïnvloed door uitschieters.

Samenvatting

Hier volgt een korte samenvatting van de belangrijkste punten die in dit artikel worden behandeld:

• De mediaan vertegenwoordigt de middelste waarde in een dataset.
• De mediaan is belangrijk omdat deze ons een idee geeft van waar de centrale waarde in een dataset ligt.
• De mediaan is doorgaans nuttiger om te berekenen dan het gemiddelde als een verdeling scheef is en/of uitschieters heeft.

Aanvullende bronnen

Concrete voorbeelden: gebruik van gemiddelde, mediaan en modus
Wanneer moet u gemiddelde vs. Mediaan: met voorbeelden
Waarom is modus belangrijk in statistieken?