Waarom is modus belangrijk in statistieken?

De modus vertegenwoordigt de waarde die het vaakst voorkomt in een gegevensset.

Een dataset kan geen modi hebben (als er geen waarden worden herhaald), één modus of meerdere modi.

De modus in de volgende gegevensset is bijvoorbeeld 19:

Gegevensset: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26

Dit is de waarde die het vaakst voorkomt.

In de statistiek is de modus belangrijk om de volgende redenen:

Reden 1 : Hierdoor weten we welke waarde(n) in een dataset het meest voorkomt.

Reden 2 : Het is nuttig om de meest voorkomende waarde in categorische gegevens te vinden wanneer het gemiddelde en de mediaan niet kunnen worden berekend.

Reden 3 : Het geeft ons een idee van waar het ‘centrum’ van een dataset zich bevindt, ook al worden de mediaan en het gemiddelde vaker gebruikt (zoals we later in dit artikel zullen zien).

De volgende voorbeelden illustreren elk van deze redenen in de praktijk.

Reden 1: De modus vertelt ons welke waarde het meest voorkomt

Laten we zeggen dat we een dataset van 100.000 rijen hebben met de verkoopprijzen van huizen in de Verenigde Staten:

Stel dat we statistische software (zoals Excel , R , Python , etc.) gebruiken om de modus van deze dataset te berekenen en ontdekken dat er drie modi zijn:

• $ 280.000
• $ 300.000
• $ 305.000

Dit geeft ons meteen een beeld van de meest voorkomende huizenprijzen in de dataset.

Het berekenen van de modusduizenden is ook veel sneller dan het bekijken van rijen gegevens en proberen vast te stellen welke huizenprijzen het vaakst voorkomen.

Reden 2: De modus zoekt naar de meest voorkomende waarde in categorische gegevens

Stel dat we een dataset van 1000 rijen hebben die ons de kleur vertelt van de auto die eigendom is van individuen in een bepaalde buurt:

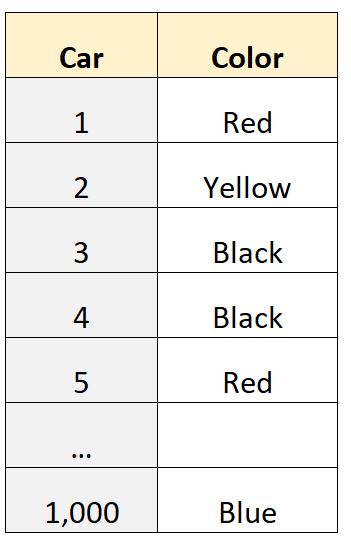
De variabele „kleur“ is eencategorische variabele , wat betekent dat de waarden tot categorieën behoren („rood“, „geel“, „zwart“, enz.) en daarom kunnen we geen kwantitatieve waarde zoals het gemiddelde of de mediaan berekenen .

We kunnen de modus echter berekenen omdat deze eenvoudigweg de meest voorkomende waarde in de dataset vertegenwoordigt.

We zouden bijvoorbeeld statistische software kunnen gebruiken om te bepalen dat de modus van deze dataset ‚zwart‘ is, wat ons vertelt dat de meest voorkomende autokleur in deze dataset zwart is.

Reden 3: Modus geeft ons een idee waar het centrum van een dataset zich bevindt

De modus wordt ook beschouwd als een maatstaf voor de centrale tendens , wat betekent dat het ons een idee kan geven van waar het ‘centrum’ van de dataset zich bevindt.

Stel dat we bijvoorbeeld de volgende dataset hebben die de examenscores van 20 verschillende studenten in een klas toont:

De modus blijkt 82 te zijn – dit is de meest voorkomende examenscore. Dit blijkt ook een goede indicatie te zijn van waar de “kern” beoordelingsscore in deze dataset ligt.

Stel echter dat we in plaats daarvan de volgende dataset met examenresultaten hebben:

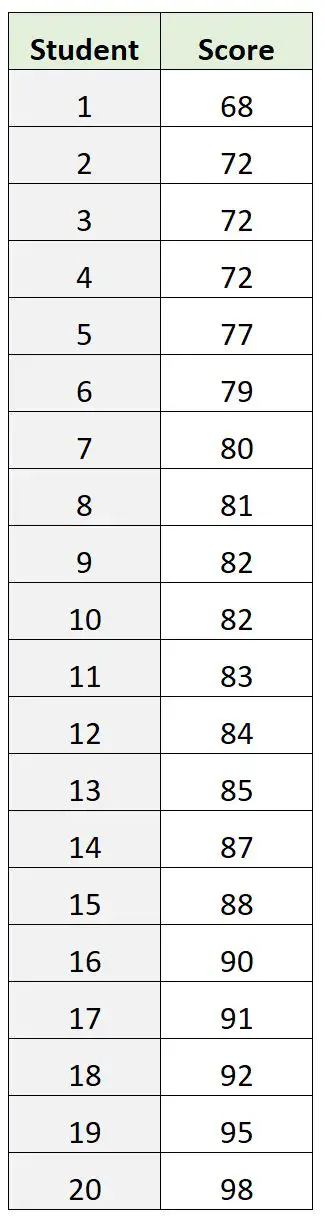
In deze dataset is 72 de score voor het mode-examen. Dit blijkt echter een slechte indicatie te zijn van waar de ‘kern’-score van het examen ligt.

De gemiddelde examenscore is 82,9 en de mediane examenscore is 82,5 , die ons beide een beter idee geven waar de ‘centrale’ waarde ligt in relatie tot de mode.

Samenvatting

Hier volgt een korte samenvatting van de belangrijkste punten die in dit artikel worden behandeld:

• De modus vertegenwoordigt de waarde(n) die het vaakst voorkomen in een dataset.
• De modus vertelt ons de meest voorkomende waarde in categorische gegevens wanneer het gemiddelde en de mediaan niet kunnen worden gebruikt.
• De modus geeft ons een idee van waar het ‘centrum’ van een dataset zich bevindt, maar kan misleidend zijn in vergelijking met het gemiddelde of de mediaan.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over gemiddelde, mediaan en modus in statistieken:

Waarom is het gemiddelde belangrijk in statistieken?
Waarom is de mediaan belangrijk in statistieken?
Concrete voorbeelden: gebruik van gemiddelde, mediaan en modus
Wanneer moet u gemiddelde vs. Mediaan: met voorbeelden