Het belang van statistieken in het onderwijs (met voorbeelden)

Het vakgebied statistiek houdt zich bezig met het verzamelen, analyseren, interpreteren en presenteren van gegevens.

In de onderwijscontext zijn statistieken belangrijk om de volgende redenen:

Reden 1 : Statistieken stellen docenten in staat de prestaties van leerlingen te begrijpen met behulp van beschrijvende statistieken.

Reden 2 : Statistieken stellen docenten in staat trends in de prestaties van leerlingen te ontdekken met behulp van datavisualisaties.

Reden 3 : Statistieken stellen docenten in staat verschillende lesmethoden met elkaar te vergelijken door middel van het testen van hypothesen.

In de rest van dit artikel bespreken we elk van deze redenen.

Reden 1: Begrijp de prestaties van leerlingen met behulp van beschrijvende statistieken

Beschrijvende statistieken worden gebruikt om gegevens te beschrijven .

In een onderwijscontext kan een leraar de volgende beschrijvende statistieken berekenen voor de leerlingen in zijn klas:

• De gemiddelde score op een bepaald examen.
• De standaardafwijking van scores op een bepaald examen.
• Het bereik van scores op een bepaald examen.
• Het percentage studenten dat geslaagd is voor een bepaald examen.
• Het 90e percentiel van de resultaten op een bepaald examen.

Dankzij deze metingen kan de leraar de resultaten van de leerlingen in zijn klas op een bepaald examen beter begrijpen.

Ze kan dan beslissen of ze haar lesmethode wil veranderen als te weinig studenten slagen voor het examen, of eventueel extra bijlesmogelijkheden wil bieden aan studenten met slechte examenresultaten, enz.

Opmerking : dit soort beschrijvende statistieken worden op alle onderwijsniveaus gebruikt. Een directeur kan bijvoorbeeld beschrijvende statistieken gebruiken om de toetsscores van leerlingen van een hele school te monitoren. Een staatsdepartement van onderwijs kan ook beschrijvende statistieken gebruiken om testscores voor studenten in een hele staat te controleren.

Reden 2: Ontdek trends met behulp van datavisualisatie

Een andere veelgebruikte manier om statistieken in het onderwijs te gebruiken is het visualiseren van gegevens zoals lijngrafieken, histogrammen, boxplots, cirkeldiagrammen en andere grafieken.

Dit soort grafieken wordt vaak gebruikt om docenten te helpen trends in de prestaties van de klas en de prestaties van individuele leerlingen te ontdekken.

Stel bijvoorbeeld dat een docent het volgende staafdiagram maakt om de gemiddelde examenscore gedurende het jaar te visualiseren:

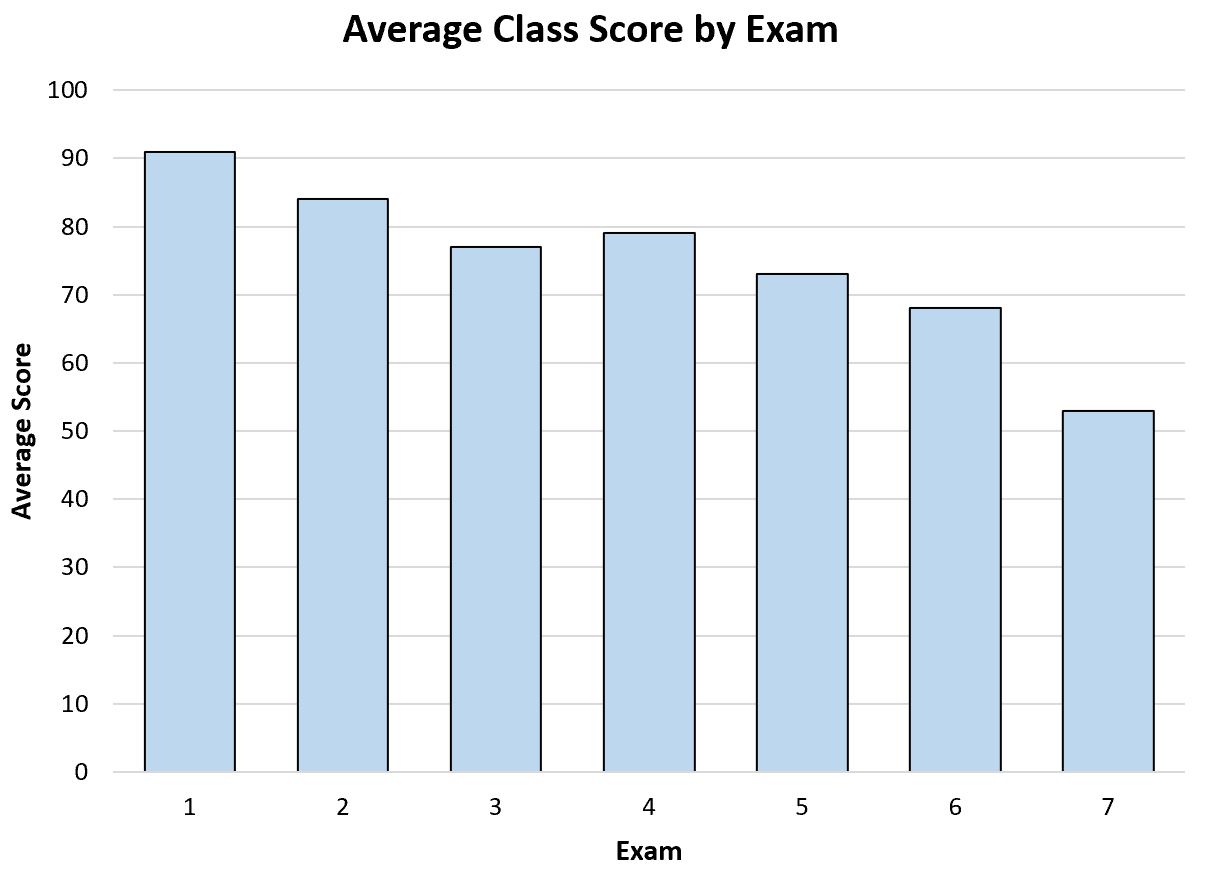
Alleen al door naar dit staafdiagram te kijken, kan de leraar zien dat de gemiddelde toetsscore van de leerlingen in zijn klas in de loop van het jaar langzaam afneemt.

Dit kan de leraar in staat stellen zijn lesmethoden te verbeteren of misschien zijn leerlingen een enquête te geven om hun mening over zijn lesmethoden te vragen, enz.

Reden 3: Vergelijk lesmethoden met behulp van hypothesetoetsing

Ook in het onderwijs wordt statistiek gebruikt in de vorm van het toetsen van hypothesen .

Dit zijn tests die docenten kunnen gebruiken om te bepalen of er statistische significantie bestaat tussen verschillende lesmethoden.

Stel bijvoorbeeld dat een docent wil bepalen of een bepaald leerplan invloed heeft op de toetsscores. Om dit te testen selecteert hij willekeurig 15 studenten die een voortest doen. Vervolgens laat hij elke leerling het leerplan een maand lang gebruiken en vervolgens een posttest met vergelijkbare moeilijkheidsgraad.

De testresultaten voor elk van de 15 studenten worden hieronder weergegeven:

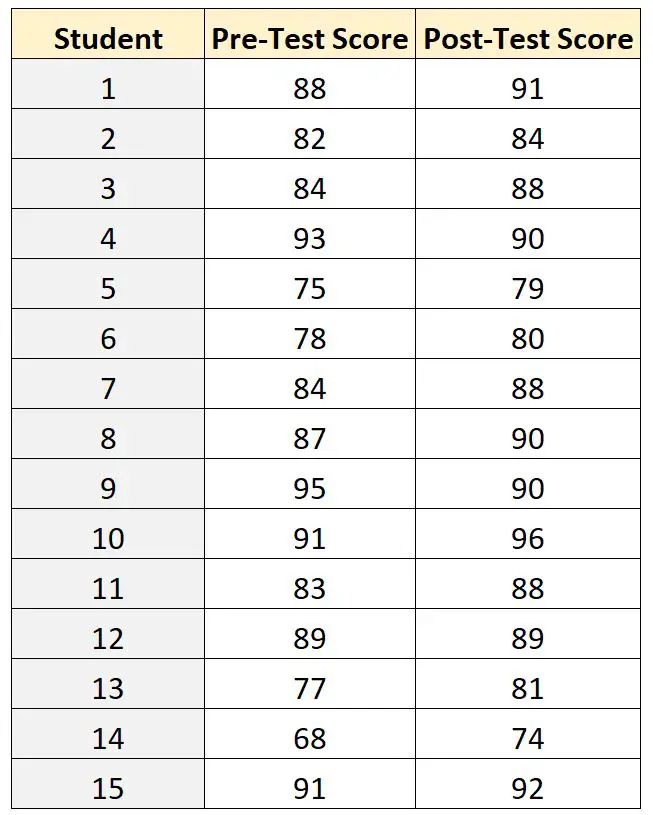
Om het verschil tussen de gemiddelde scores vóór en na de test te vergelijken, kan de docent gepaarde t-teststeekproeven gebruiken, omdat voor elke leerling de pre-testscore kan worden gekoppeld aan de post-testscore.

Stel dat de professor statistische software gebruikt om deze paired-samples t-test uit te voeren en de volgende resultaten ontvangt:

• t-teststatistiek: -2,97
• p-waarde: 0,0101

In dit voorbeeld gebruikt de t-test van gepaarde monsters de volgende nul- en alternatieve hypothesen:

• H ₀ : De gemiddelde pre-test- en post-testscores zijn gelijk
• H _A : De gemiddelde pre-test- en post-testscores zijn niet gelijk

Omdat de p-waarde ( 0,0101 ) kleiner is dan 0,05, verwerpen we de nulhypothese.

Dit betekent dat we voldoende bewijs hebben om te zeggen dat de gemiddelde toetsscore verschillend is voor studenten voor en na deelname aan de opleiding.

Opmerking : dit is slechts één voorbeeld van het testen van hypothesen dat in het onderwijs wordt gebruikt. Andere veel voorkomende tests zijn onder meer een t-test met één monster , een t-test met twee monsters , eenrichtings-ANOVA en een tweerichtings-ANOVA .

Aanvullende bronnen

In de volgende artikelen wordt het belang van statistieken op andere gebieden uitgelegd:

Het belang van statistieken in bedrijven
Het belang van statistiek in de economie
Het belang van statistiek in de gezondheidszorg