Hoe bemonsteringsverdelingen in r te berekenen

Een steekproefverdeling is een waarschijnlijkheidsverdeling van een bepaalde statistiek gebaseerd op veel willekeurige steekproeven uit één populatie.

In deze zelfstudie wordt uitgelegd hoe u het volgende kunt doen met steekproefverdelingen in R:

• Genereer een steekproefverdeling.
• Visualiseer de steekproefverdeling.
• Bereken het gemiddelde en de standaardafwijking van de steekproefverdeling.
• Bereken de kansen met betrekking tot de steekproefverdeling.

Genereer een steekproefverdeling in R

De volgende code laat zien hoe u een steekproefverdeling in R genereert:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

In dit voorbeeld hebben we de functie rnorm() gebruikt om het gemiddelde van 10.000 steekproeven te berekenen waarin elke steekproefomvang 20 was en werd gegenereerd op basis van een normale verdeling met een gemiddelde van 5,3 en een standaarddeviatie van 9.

We kunnen zien dat het eerste monster een gemiddelde van 5,283992 had, het tweede monster een gemiddelde van 6,304845, enzovoort.

Visualiseer de steekproefverdeling

De volgende code laat zien hoe u een eenvoudig histogram maakt om de steekproefverdeling te visualiseren:

 #create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

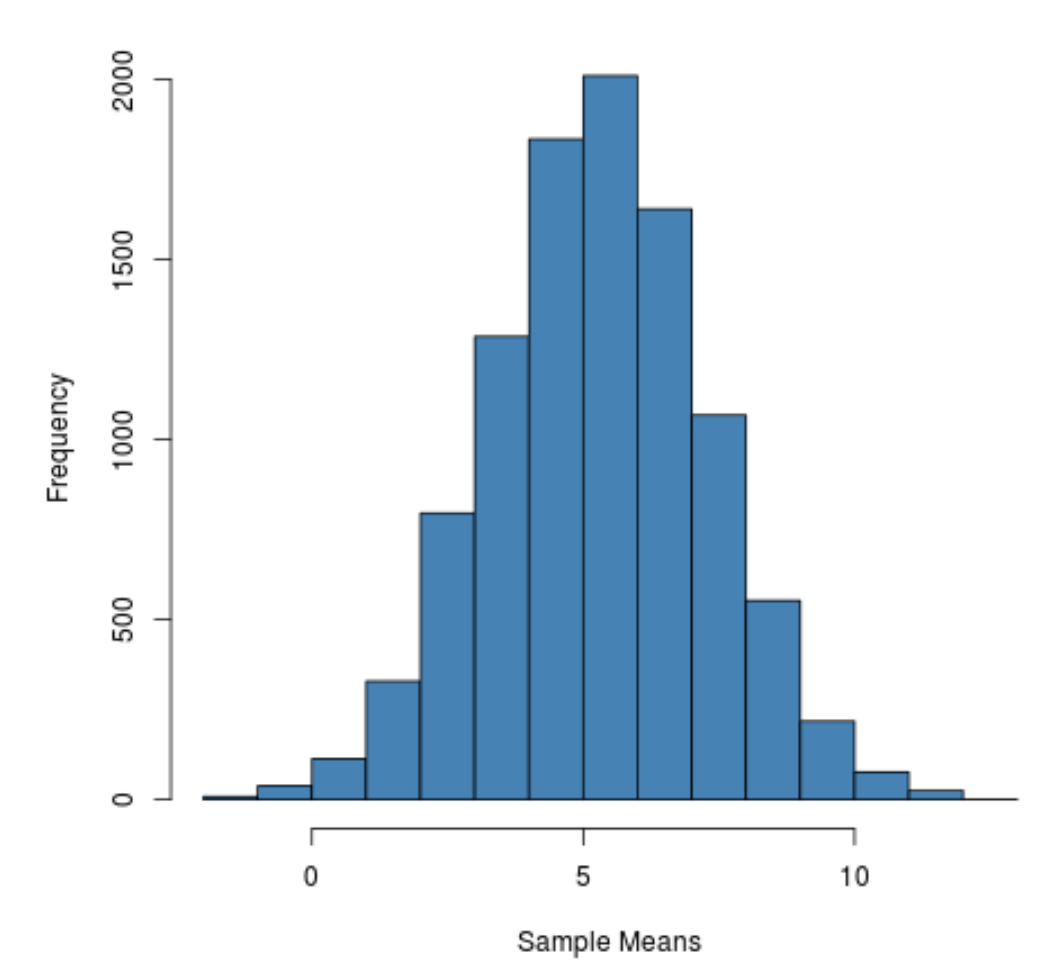
Het is te zien dat de steekproefverdeling klokvormig is met een piek nabij de waarde 5.

Aan de staarten van de verdeling kunnen we echter zien dat sommige steekproeven gemiddelden groter dan 10 hadden en andere gemiddelden kleiner dan 0.

Zoek het gemiddelde en de standaarddeviatie

De volgende code laat zien hoe u het gemiddelde en de standaardafwijking van de steekproefverdeling kunt berekenen:

 #mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

Theoretisch zou het gemiddelde van de steekproefverdeling 5,3 moeten zijn. We kunnen zien dat het werkelijke steekproefgemiddelde in dit voorbeeld 5,287195 is, wat dicht bij 5,3 ligt.

En theoretisch zou de standaardafwijking van de steekproefverdeling gelijk moeten zijn aan s/√n, wat 9 / √20 = 2,012 zou zijn. We kunnen zien dat de werkelijke standaardafwijking van de steekproefverdeling 2,00224 is, wat dichtbij 2,012 ligt.

Bereken de kansen

De volgende code laat zien hoe u de waarschijnlijkheid kunt berekenen dat een bepaalde waarde voor een steekproefgemiddelde wordt verkregen, gegeven een populatiegemiddelde, de populatiestandaarddeviatie en de steekproefomvang.

 #calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

In dit specifieke voorbeeld vinden we de waarschijnlijkheid dat het steekproefgemiddelde kleiner is dan of gelijk is aan 6, gegeven het feit dat het populatiegemiddelde 5,3 is, de standaarddeviatie van de populatie 9 is en de omvang van de steekproef van 20 0,6417 is.

Dit komt zeer dicht in de buurt van de waarschijnlijkheid berekend door de Sampling Distribution Calculator :

De volledige code

De volledige R-code die in dit voorbeeld wordt gebruikt, wordt hieronder weergegeven:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

Aanvullende bronnen

Een inleiding tot bemonsteringsverdelingen
Bemonsteringsdistributiecalculator
Een inleiding tot de centrale limietstelling