Een gids voor de benjamini-hochberg-procedure

Elke keer dat u een statistische test uitvoert, is het mogelijk dat u door puur toeval een p-waarde van minder dan 0,05 krijgt, zelfs als uw nulhypothese waar is.

Stel dat u bijvoorbeeld wilt weten of een bepaalde plant een gemiddelde hoogte van meer dan 25 cm heeft. Uw nul- en alternatieve hypothesen voor testen zouden zijn:

_H0 : μ = 10 inch

H _A : μ > 10 inch

Om deze hypothese te testen, kun je op pad gaan en een willekeurige steekproef van twintig planten verzamelen om te meten. Hoewel de werkelijke gemiddelde hoogte van deze plantensoort 25 cm bedraagt, is het mogelijk dat u een steekproef van twintig ongewoon hoge planten heeft geselecteerd, waardoor u de nulhypothese verwerpt.

Zelfs als de nulhypothese waar zou zijn (de gemiddelde hoogte van deze plant was eigenlijk 25 cm), verwierp je deze. In de statistieken noemen we dit een ‘valse ontdekking’. U beweert een ontdekking te hebben gedaan – een “significant resultaat” – maar dit is feitelijk onjuist.

Stel je nu voor dat je 100 statistische tests tegelijk uitvoert. Bij een alfaniveau van 0,05 is de kans op een valse ontdekking bij een individuele test slechts 5%, maar omdat je zo’n groot aantal tests doet, zou je verwachten dat slechts ongeveer 5 op de 100 tot valse ontdekkingen leiden.

In de moderne wereld kunnen valse ontdekkingen een veelvoorkomend probleem zijn, omdat de technologie onderzoekers in staat heeft gesteld honderden of zelfs duizenden statistische tests tegelijk uit te voeren.

Medische onderzoekers kunnen bijvoorbeeld statistische tests uitvoeren op tienduizenden genen tegelijk. Zelfs met een percentage valse ontdekkingen van slechts 5% betekent dit dat honderden tests tot valse ontdekkingen kunnen leiden.

Eén manier om het aantal valse ontdekkingen onder controle te houden, is door gebruik te maken van de zogenaamde Benjamini-Hochberg-procedure.

De Benjamini-Hochberg-procedure

De Benjamini-Hochberg-procedure werkt als volgt:

Stap 1: Voer al uw statistische tests uit en vind de p-waarde voor elke test.

Stap 2: Rangschik de p-waarden in aflopende volgorde, waarbij u aan elke waarde een rangorde toekent: de kleinste waarde heeft een rangorde van 1, de volgende kleinste heeft een rangorde van 2, enz.

Stap 3: Bereken de kritische Benjamini-Hochberg-waarde voor elke p-waarde, met behulp van de formule (i/m)*Q

Goud:

i = rang van p-waarde

m = totaal aantal tests

Q = het door u gekozen percentage valse ontdekkingen

Stap 4: Vind de grootste p-waarde die kleiner is dan de kritische waarde. Wijs elke p-waarde kleiner dan deze p-waarde aan als significant.

Het volgende voorbeeld illustreert hoe u deze procedure met concrete waarden kunt uitvoeren.

Voorbeeld

Laten we zeggen dat onderzoekers willen bepalen of twintig verschillende variabelen al dan niet verband houden met hartziekten. Ze voeren twintig individuele statistische tests tegelijk uit en ontvangen voor elke test een p-waarde. De volgende tabel toont de p-waarden voor elke test, gerangschikt in aflopende volgorde.

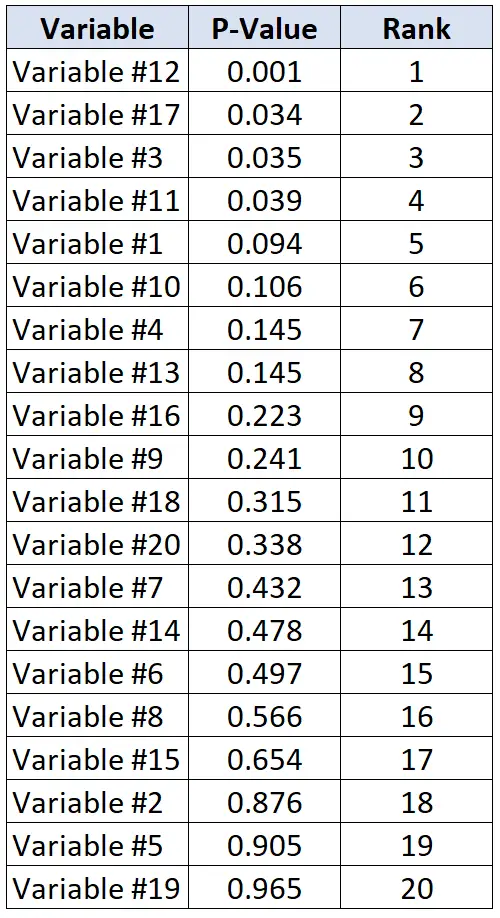
Stel dat onderzoekers bereid zijn een percentage valse ontdekkingen van 20% te accepteren. Om de kritische Benjamini-Hochberg-waarde voor elke p-waarde te berekenen, kunnen we dus de volgende formule gebruiken: (i/20)*0,2 waarbij i = rangorde van de p-waarde.

De volgende tabel toont de kritische Benjamini-Hochberg-waarde voor elke individuele p-waarde:

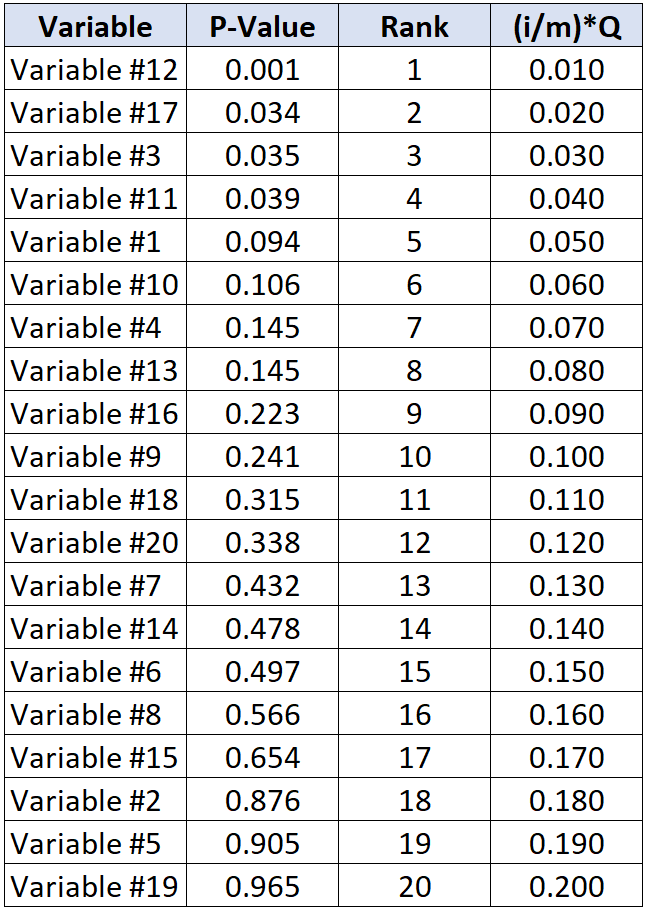
De test met de grootste p-waarde onder de kritische Benjamini-Hochberg-waarde is variabele #11, die een p-waarde heeft van 0,039 en een kritische BH-waarde van 0,040.

Deze test en alle tests met een kleinere p-waarde worden dus als significant beschouwd.

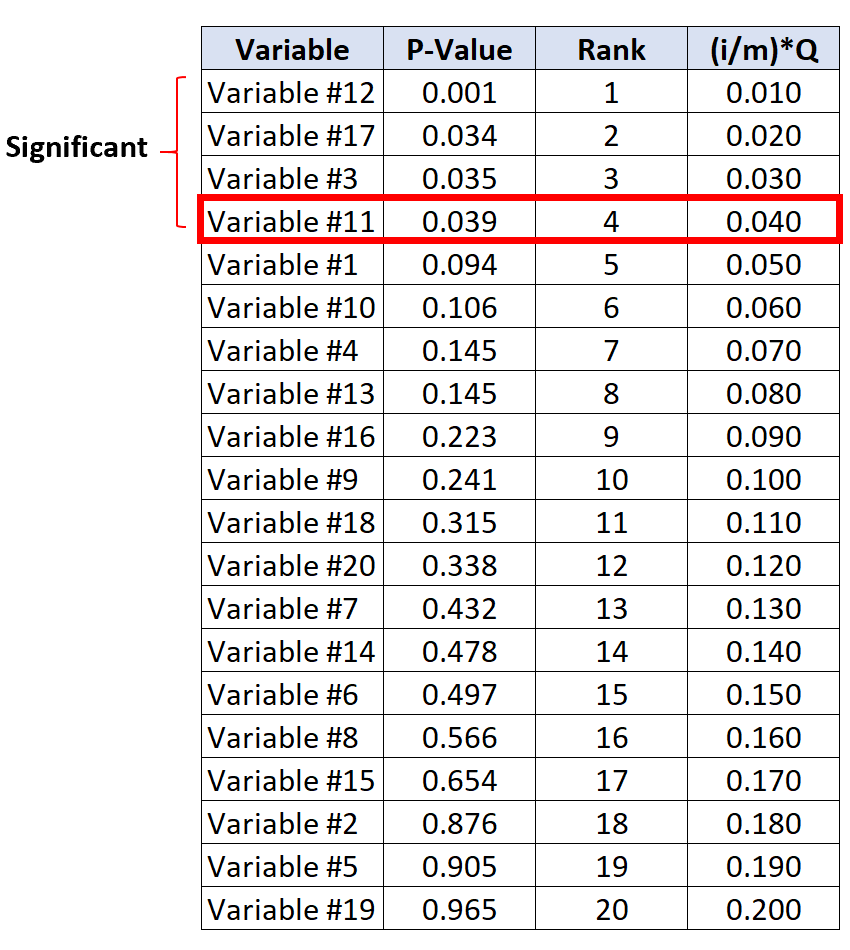
Merk op dat hoewel variabelen #17 en #3 geen p-waarden hadden die kleiner waren dan hun BH-kritische waarden, ze nog steeds als significant worden beschouwd omdat ze kleinere p-waarden hebben dan variabele #11.

Hoe u een valse detectiepercentage kiest

Een van de belangrijkste stappen in de Benjamini-Hochberg-procedure is het kiezen van een percentage valse ontdekkingen. U moet uw valse ontdekkingspercentage kiezen voordat u gegevens verzamelt of statistische tests uitvoert.

Normaal gesproken voert u tijdens de verkennende fase van uw analyse een groot aantal statistische tests uit, die u vervolgens zult opvolgen met andere tests om uw resultaten verder te onderzoeken.

Als vervolgtesten niet duur zijn, kunt u overwegen een hoger percentage valse ontdekkingen in te stellen, want zelfs als u een paar valse ontdekkingen doet, zult u deze valse ontdekkingen waarschijnlijk bij volgende tests ontdekken.

Als de kosten voor het missen van een belangrijke ontdekking hoog zijn, kunt u bovendien uw percentage valse ontdekkingen verhogen, zodat u niets belangrijks mist.

Afhankelijk van de kosten van uw onderzoek en het belang om geen belangrijke bevindingen te missen, varieert het percentage valse ontdekkingen van situatie tot situatie.

Aanvullende bronnen

Een uitleg van P-waarden en statistische significantie
Wat is het foutenpercentage per gezin?