Wat is reikwijdtebeperking?

Vaak proberen we in de statistiek de correlatie tussen twee variabelen te meten. Dit helpt ons het volgende te begrijpen:

• De richting van de relatie tussen twee variabelen. Als de ene variabele toeneemt, heeft de andere variabele dan de neiging toe te nemen of af te nemen?
• De sterkte van de relatie tussen twee variabelen. Hoeveel verandert de waarde van de twee variabelen?

Helaas wordt een probleem dat kan optreden bij het meten van de correlatie tussen twee variabelen bereikbeperking genoemd. Dit gebeurt wanneer het bereik van meetwaarden voor een van de variabelen om een of andere reden beperkt is.

Stel dat we bijvoorbeeld de correlatie willen meten tussen studie-uren en examenscores van leerlingen op een bepaalde school.

Als we gegevens over deze twee variabelen verzamelen voor alle 1.000 leerlingen op school, kunnen we vaststellen dat de correlatie tussen de gestudeerde uren en de examenscores 0,73 bedraagt.

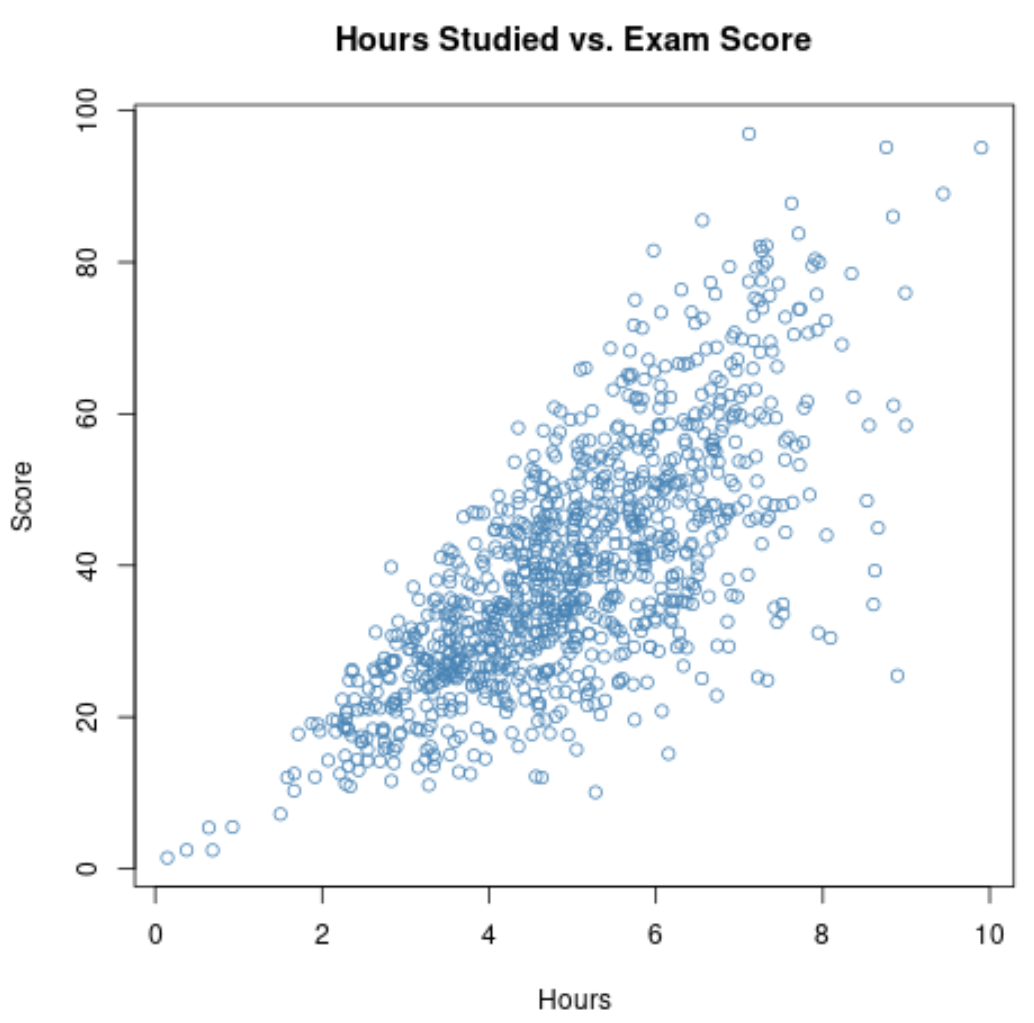
Deze correlatie is vrij hoog, wat wijst op een sterke positieve relatie tussen de twee variabelen. Naarmate studenten meer studeren, presteren ze doorgaans beter op examens.

Laten we er echter vanuit gaan dat wij alleen gegevens verzamelen over studenten in honourscursussen. Het kan zijn dat al deze studenten minimaal 6 uur hebben gestudeerd.

Als we dus de correlatie tussen de gestudeerde uren en de examenscores voor deze studenten berekenen, gebruiken we een smal bereik voor variabele gestudeerde uren .

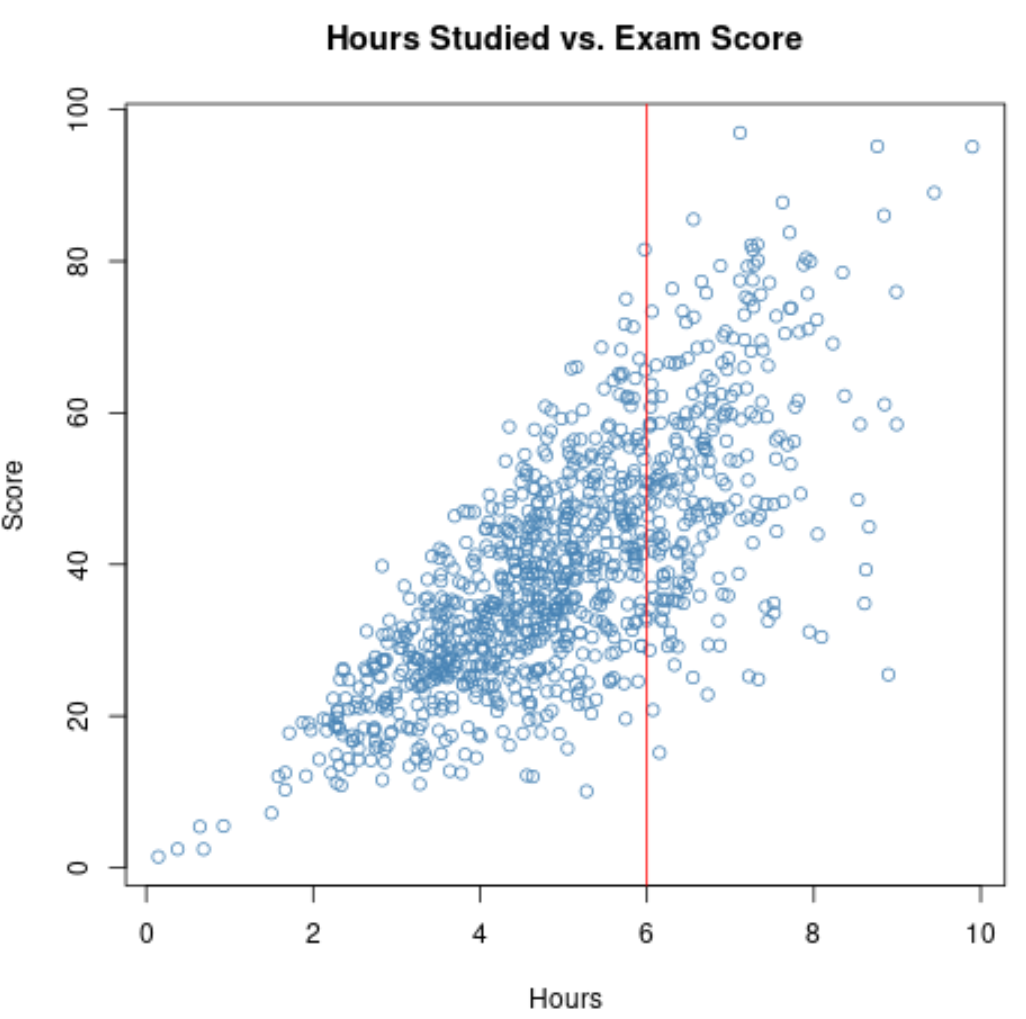
Als we inzoomen op het spreidingsdiagram voor het bereik waar de uren groter zijn dan 6, ziet het diagram er zo uit:

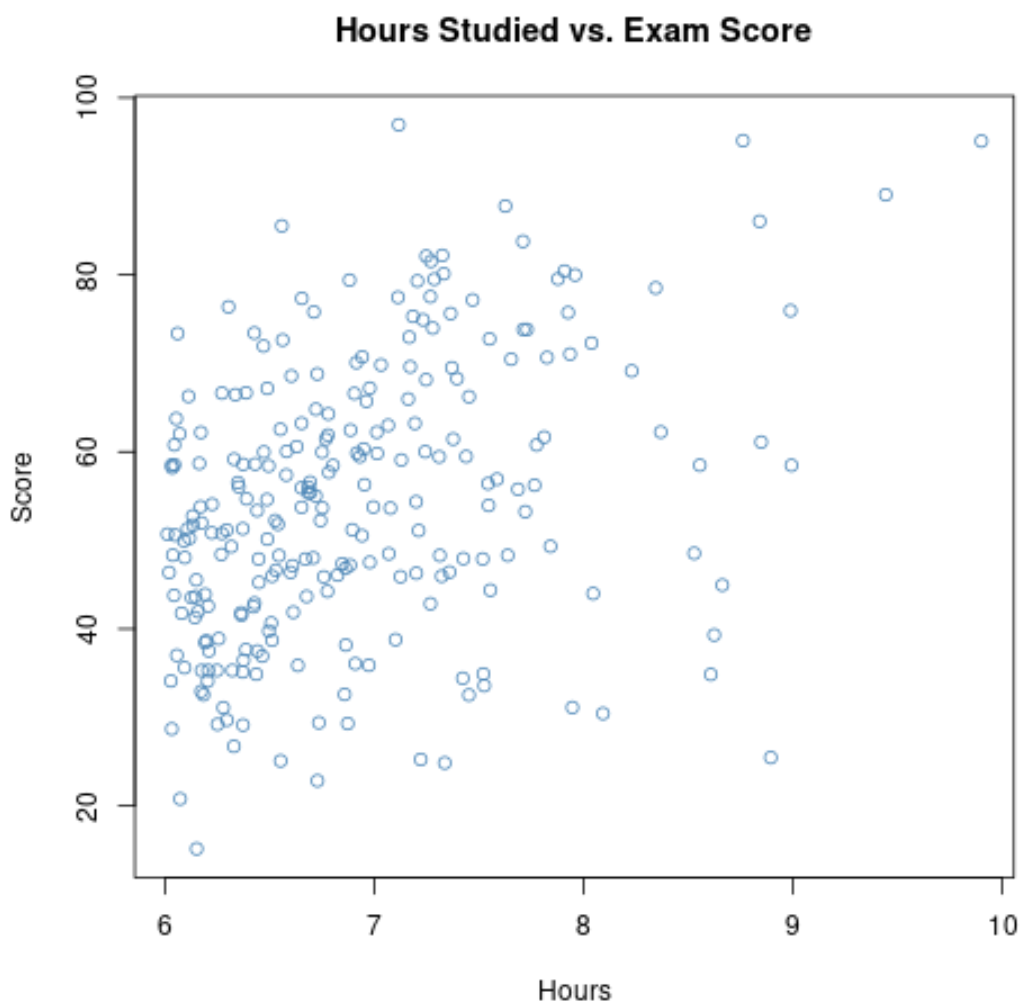
De correlatie tussen de twee variabelen in deze grafiek blijkt 0,37 te zijn, wat aanzienlijk lager is dan 0,73 .

Als we dus alleen gegevens zouden verzamelen over de studie-uren en examenscores van studenten in honourscursussen, zouden we kunnen aannemen dat er een zwakke relatie bestaat tussen de studie-uren en examenscores.

Dit resultaat zou echter misleidend zijn omdat we voor een van de variabelen een beperkt bereik hebben gebruikt.

Voorbeelden uit de praktijk van een beperkt bereik

Het probleem van een beperkt bereik kan zich in de praktijk in veel verschillende onderzoeken voordoen. Hier zijn enkele voorbeelden:

1. Onderzoek naar topsporters . Onderzoekers zijn wellicht geïnteresseerd om te onderzoeken of een bepaald trainingsprogramma meer spiermassa oplevert dan een bepaald standaardprogramma.

Als onderzoekers alleen gegevens verzamelen over topsporters, is het waarschijnlijk dat deze atleten allemaal al een hoge spiermassa hebben. Er zal daarom een smal bereik aan waarden beschikbaar zijn om de correlatie tussen trainingsprogramma en geproduceerde spiermassa te berekenen.

2. Studies van goed presterende studenten. Onderzoekers willen misschien onderzoeken of een bepaald bijlesprogramma al dan niet een positief effect heeft op de cijfers. Studenten die graag hun cijfers willen verbeteren en willen deelnemen aan het bijlesprogramma, kunnen van nature al goed presterende studenten zijn.

Er is dus misschien niet veel ruimte voor verbetering in de cijfers van deze studenten. Wanneer onderzoekers de correlatie berekenen tussen de uren besteed aan het bijlesprogramma en de daaruit voortvloeiende cijferverhoging, wordt de werkelijke correlatie mogelijk onderschat omdat de ruimte voor cijferverbetering beperkt is.

Hoe u rekening kunt houden met beperkte bereiken

Een populaire manier om rekening te houden met beperkte bereiken staat bekend als de Thorndike Case 2 , een formule ontwikkeld door psychometrist Robert L. Thorndike.

Deze formule geeft een schatting van de werkelijke correlatie tussen twee variabelen en gebruikt de volgende berekening:

Ware correlatie = √(1-(SD ² _{y beperkt} -SD ² _{y onbeperkt} )) * (1-r ² _beperkt )

Goud:

• SD ² _{beperkt y} : De gekwadrateerde standaardafwijking van de beschikbare gegevens over de responsvariabele y.
• _Onbeperkte SD ² jaar: De bekende gekwadrateerde standaarddeviatie van de responsvariabele voor de populatie.
• r ² _beperkt : De kwadratische correlatie op de beperkte beschikbare gegevens.

Het is aangetoond dat deze formule effectief is bij het produceren van onbevooroordeelde schattingen van de werkelijke correlatie tussen twee variabelen wanneer een van de variabelen binnen een beperkt bereik valt.

Houd er rekening mee dat u, om deze formule te gebruiken, een schatting moet hebben van de werkelijke standaarddeviatie van de populatie voor de responsvariabele.