Hoe een waarschijnlijkheid te vinden gegeven een gemiddelde en een standaarddeviatie

We kunnen het volgende proces gebruiken om de waarschijnlijkheid te vinden van een normaal verdeelde willekeurige variabele

Stap 1: Zoek de z-score.

Een z-score vertelt u hoeveel standaarddeviaties een individuele gegevenswaarde van het gemiddelde afwijkt. Het wordt als volgt berekend:

z-score = (x – μ) / σ

Goud:

• x: individuele gegevenswaarde
• μ: populatiegemiddelde
• σ: standaarddeviatie van de populatie

Stap 2: Vind de waarschijnlijkheid die overeenkomt met de z-score.

Nadat we de z-score hebben berekend, kunnen we de overeenkomstige waarschijnlijkheid in de z-tabel vinden.

De volgende voorbeelden laten zien hoe u dit proces in verschillende scenario’s kunt gebruiken.

Voorbeeld 1: Waarschijnlijkheid kleiner dan een bepaalde waarde

Scores op een bepaalde toets zijn normaal verdeeld met gemiddelde μ = 82 en standaarddeviatie σ = 8. Wat is de kans dat een bepaalde leerling minder dan 84 scoort op de toets?

Stap 1: Zoek de z-score.

Eerst zullen we de z-score vinden die hoort bij een score van 84:

z-score = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Stap 2: Gebruik de z-tabel om de overeenkomstige waarschijnlijkheid te vinden.

Vervolgens gaan we op zoek naar de waarde 0,25 in de z-tabel:

De kans dat een bepaalde leerling minder dan 84 scoort is ongeveer 59,87% .

Voorbeeld 2: Waarschijnlijkheid groter dan een bepaalde waarde

De hoogte van een bepaalde pinguïnsoort is normaal verdeeld met een gemiddelde van μ = 30 inch en een standaardafwijking van σ = 4 inch. Als we willekeurig een pinguïn selecteren, hoe groot is dan de kans dat deze meer dan 75 centimeter groot zal zijn?

Stap 1: Zoek de z-score.

Eerst zullen we de z-score vinden die hoort bij een hoogte van 28 inch.

Score z = (x – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0,5

Stap 2: Gebruik de z-tabel om de overeenkomstige waarschijnlijkheid te vinden.

Vervolgens gaan we op zoek naar de waarde -0,5   in tabel z:

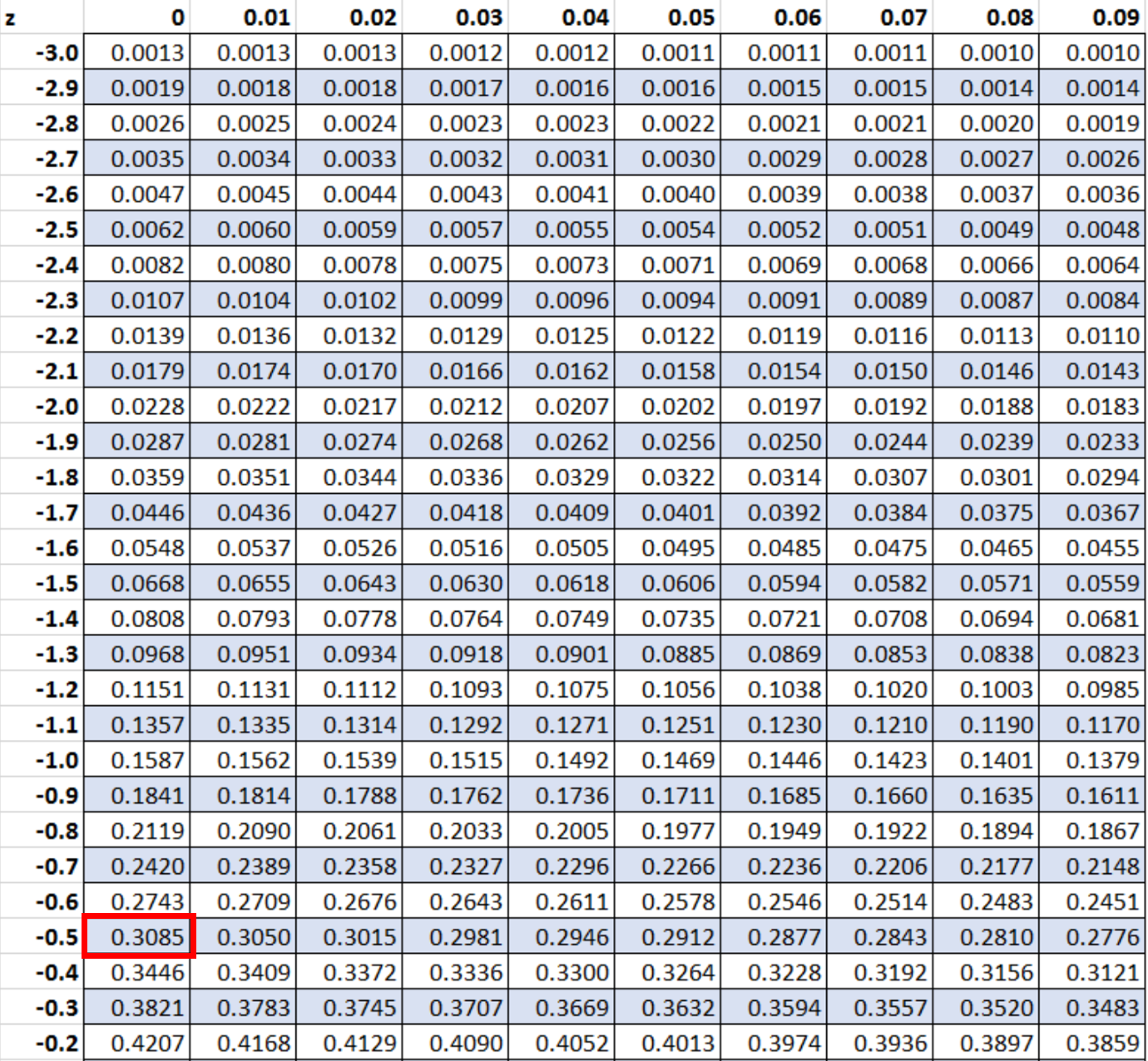
De waarde die overeenkomt met een z-score van -0,5 is 0,3085. Dit vertegenwoordigt de waarschijnlijkheid dat een pinguïn kleiner zal zijn dan 28 inch.

Omdat we echter de kans willen weten dat een pinguïn groter is dan 28 inch, moeten we die kans van 1 aftrekken.

De kans dat een pinguïn groter is dan 28 inch is dus: 1 – 0,3085 = 0,6915 .

Voorbeeld 3: Waarschijnlijkheid tussen twee waarden

Het gewicht van een bepaalde soort schildpad is normaal verdeeld met een gemiddelde van μ = 400 pond en een standaardafwijking van σ = 25 pond. Als we willekeurig een schildpad selecteren, wat is dan de kans dat deze tussen de 410 en 425 pond weegt?

Stap 1: Zoek de z-scores.

Eerst zullen we de z-scores vinden die horen bij 410 boeken en 425 boeken

z-score van 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

z-score van 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Stap 2: Gebruik de z-tabel om de overeenkomstige waarschijnlijkheid te vinden.

Eerst gaan we op zoek naar de waarde 0,4   in tabel z:

Vervolgens gaan we op zoek naar de waarde 1   in tabel z:

Vervolgens trekken we de kleinere waarde af van de grotere waarde: 0,8413 – 0,6554 = 0,1859 .

Dus de kans dat een willekeurig geselecteerde schildpad tussen de 410 pond en 425 pond weegt, is 18,59% .

Aanvullende bronnen

Hoe u handmatig een P-waarde kunt berekenen op basis van een Z-score
Hoe Z-scores naar ruwe scores te converteren
Hoe Z-scores in een bepaald gebied te vinden