Hoe u de waarschijnlijkheid kunt vinden op basis van een z-score: met voorbeelden

De eenvoudigste manier om de waarschijnlijkheid uit een z-score te bepalen, is door eenvoudigweg de waarschijnlijkheid te vinden die overeenkomt met de z-score in de z-tabel.

In deze tutorial wordt uitgelegd hoe u de z-tabel gebruikt om de volgende kansen te vinden:

• De kans dat een waarde onder een bepaalde z-score ligt.
• De kans dat een waarde groter is dan een bepaalde z-score.
• De kans dat een waarde tussen twee bepaalde z-scores valt.

Laten we gaan!

Voorbeeld 1: Waarschijnlijkheid kleiner dan een bepaalde Z-score

Stel dat we de waarschijnlijkheid willen vinden dat een waarde in een bepaalde verdeling een z-score heeft die kleiner is dan z = 0,25 .

Om deze waarschijnlijkheid te vinden, moeten we in de z-tabel naar 0,25 zoeken:

De kans dat een waarde in een bepaalde verdeling een z-score heeft die kleiner is dan z = 0,25 is ongeveer 0,5987 .

Opmerking : dit kan procentueel ook worden geschreven als 59,87% .

Voorbeeld 2: Waarschijnlijkheid groter dan een bepaalde Z-score

Stel dat we de waarschijnlijkheid willen vinden dat een waarde in een bepaalde verdeling een z-score heeft die groter is dan z = -0,5 .

Om deze waarschijnlijkheid te vinden, moeten we zoeken naar -0,5 in de z-tabel:

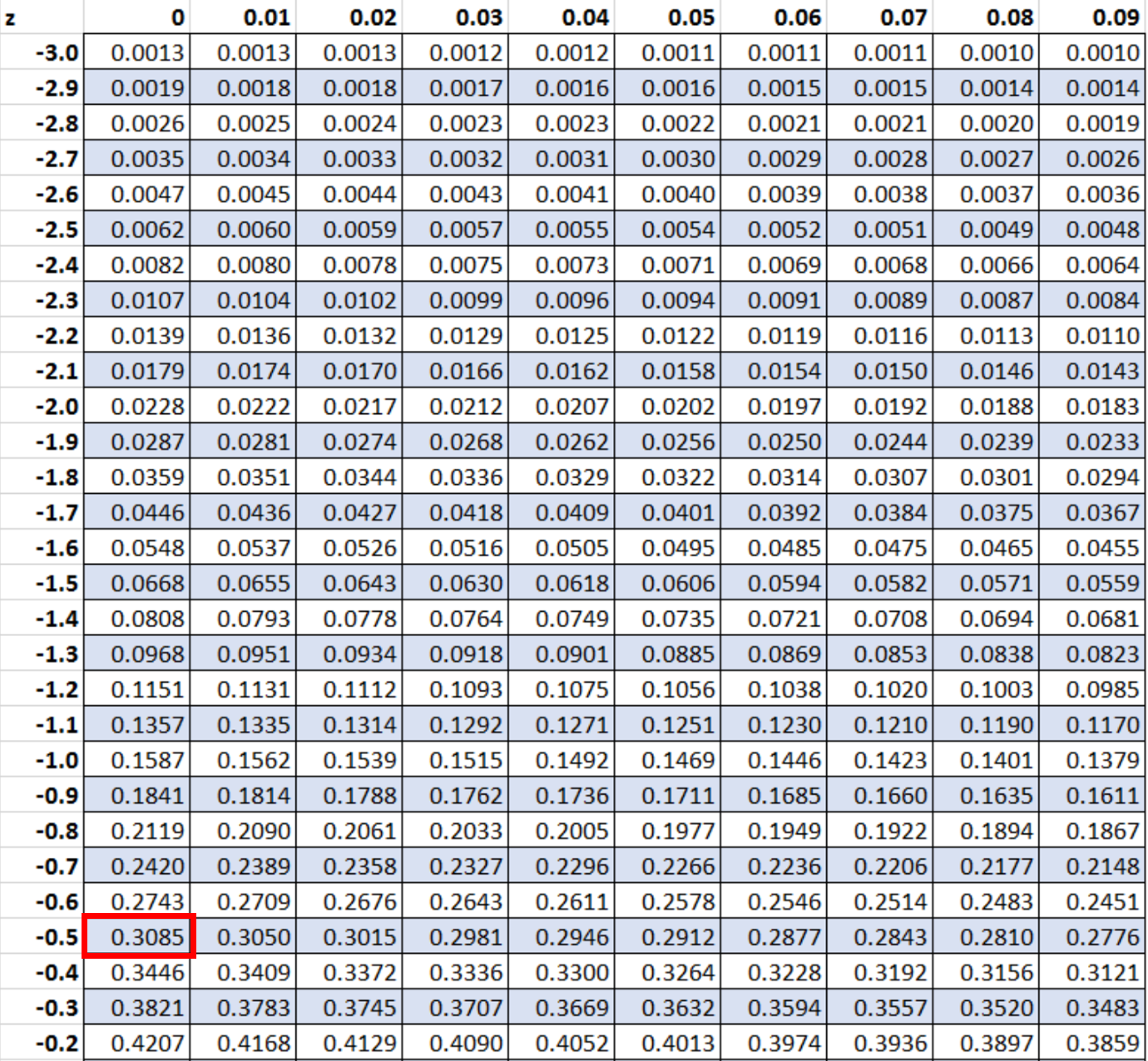
De waarschijnlijkheid die overeenkomt met een z-score van -0,5 is 0,3085.

Omdat we echter de waarschijnlijkheid willen weten dat een waarde in een bepaalde verdeling een z-score groter dan -0,5 heeft, moeten we die waarschijnlijkheid van 1 aftrekken.

De kans dat een waarde in een bepaalde verdeling een z-score groter dan -0,5 heeft, is dus: 1 – 0,3085 = 0,6915 .

Voorbeeld 3: Waarschijnlijkheid tussen twee Z-scores

Stel dat we de waarschijnlijkheid willen vinden dat een waarde in een gegeven verdeling een z-score heeft tussen z = 0,4 en z = 1 .

Eerst gaan we op zoek naar de waarde 0,4   in tabel z:

Vervolgens gaan we op zoek naar de waarde 1   in tabel z:

Vervolgens trekken we de kleinere waarde af van de grotere waarde: 0,8413 – 0,6554 = 0,1859 .

De kans dat een waarde in een bepaalde verdeling een z-score heeft tussen z = 0,4 en z = 1 is dus ongeveer 0,1859 .

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over z-scores:

5 voorbeelden van het gebruik van Z-Scores in het echte leven
Hoe Z-scores naar ruwe scores te converteren
Hoe Z-scores in een bepaald gebied te vinden