Hoe u percentielen kunt berekenen op basis van gemiddelde en standaarddeviatie

U kunt de volgende formule gebruiken om het percentiel van een normale verdeling te berekenen, gegeven een gemiddelde en een standaarddeviatie:

Percentielwaarde = μ + zσ

Goud:

• µ : Gemiddeld
• z : z-score uit de z-tabel die overeenkomt met de percentielwaarde
• σ : Standaardafwijking

De volgende voorbeelden laten zien hoe u deze formule in de praktijk kunt gebruiken.

Voorbeeld 1: Bereken het 15e percentiel met behulp van het gemiddelde en de standaarddeviatie

Stel dat het gewicht van een bepaalde ottersoort normaal verdeeld is met een gemiddelde van μ = 60 pond en een standaarddeviatie van σ = 12 pond.

Hoeveel weegt een otter op het 15e percentiel?

Om deze vraag te beantwoorden, moeten we de z-score vinden die het dichtst bij de waarde 0,15 in de z-tabel ligt. Deze waarde blijkt -1,04 te zijn:

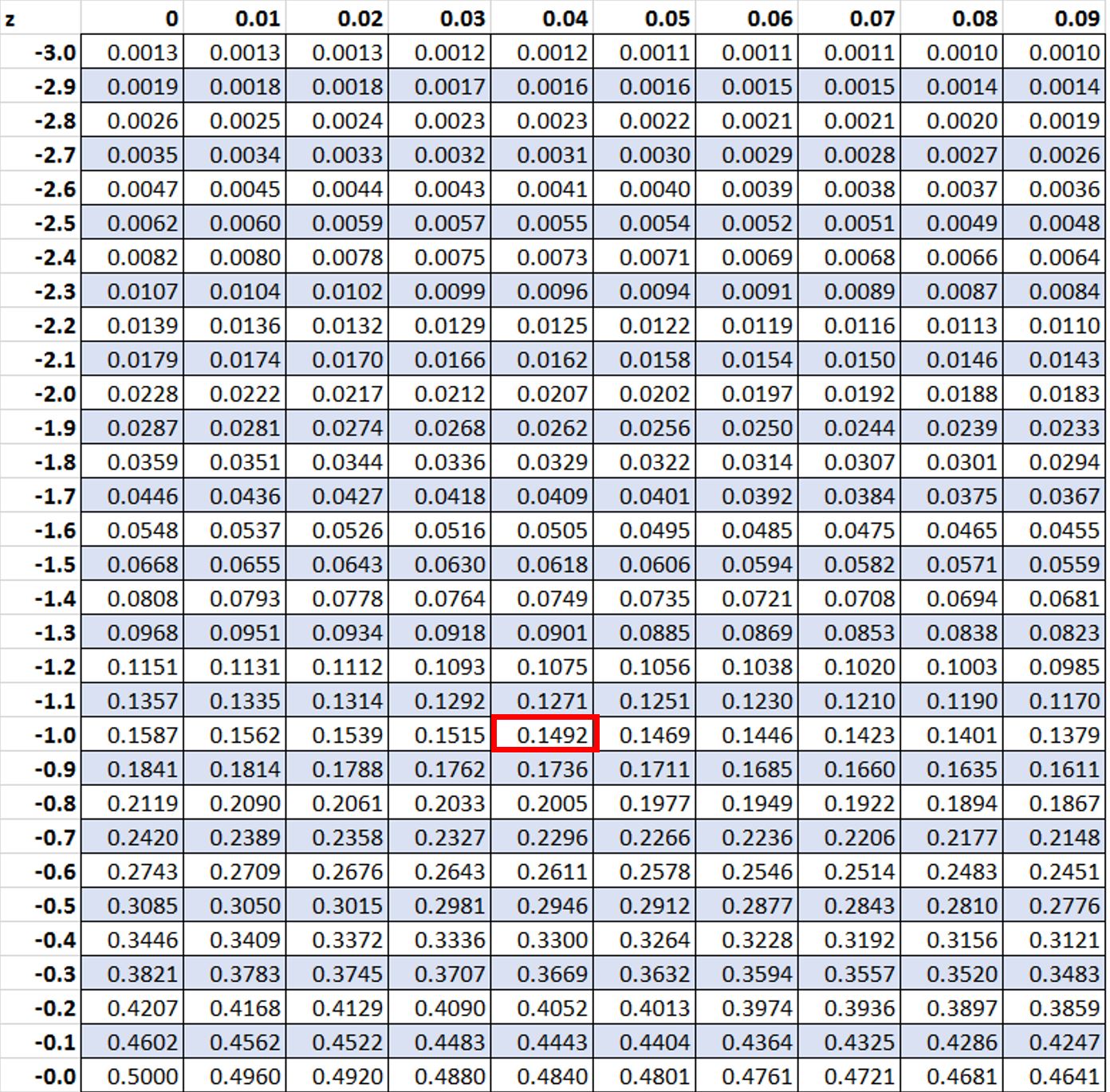
We kunnen deze waarde vervolgens in de percentielformule invoeren:

• Percentielwaarde = μ + zσ
• 15e percentiel = 60 + (-1,04)*12
• 15e percentiel = 47,52

Een otter op het 15e percentiel weegt ongeveer 47,52 pond.

Opmerking : we kunnen ook de Z-score percentielcalculator gebruiken om te bepalen dat de exacte z-score die overeenkomt met het 15e percentiel -1,0364 is.

Door deze waarde in de percentielformule in te voegen, verkrijgen we:

• Percentielwaarde = μ + zσ
• 15e percentiel = 60 + (-1,0364)*12
• 15e percentiel = 47,5632

Voorbeeld 2: Bereken het 93e percentiel met behulp van het gemiddelde en de standaarddeviatie

Stel dat de resultaten van een bepaalde test normaal verdeeld zijn met een gemiddelde van μ = 85 en een standaarddeviatie van σ = 5.

Wat is de examenscore van een student die in het 93e percentiel scoort?

Om deze vraag te beantwoorden, moeten we de z-score vinden die het dichtst bij de waarde 0,93 in de z-tabel ligt. Deze waarde blijkt 1,48 te zijn:

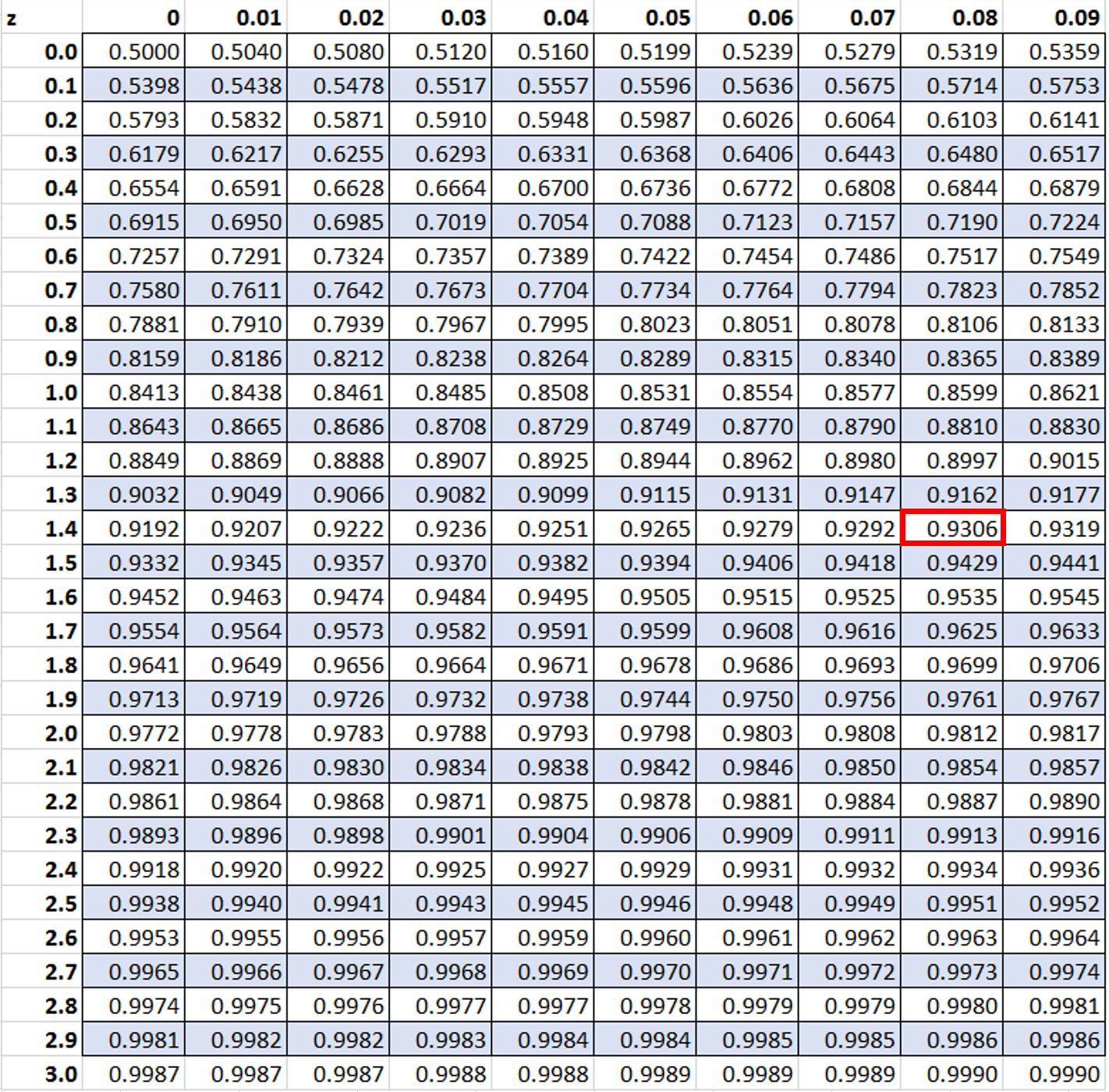
We kunnen deze waarde vervolgens in de percentielformule invoeren:

• Percentielwaarde = μ + zσ
• 93e percentiel = 85 + (1,48)*5
• 93e percentiel = 92,4

Een student die op het 93e percentiel scoort, krijgt een examencijfer van ongeveer 92,4 .

Opmerking : we kunnen ook de Z-score percentielcalculator gebruiken om te bepalen dat de exacte z-score die overeenkomt met het 93e percentiel 1,4758 is.

Door deze waarde in de percentielformule in te voegen, verkrijgen we:

• Percentielwaarde = μ + zσ
• 93e percentiel = 85+ (1,4758)*5
• 93e percentiel = 92,379

Aanvullende bronnen

Hoe de Z-tabel te gebruiken (met voorbeelden)
Hoe te converteren tussen Z-scores en percentielen in Excel