Hoe u het r-kwadraat met de hand kunt berekenen
In de statistiek meet R kwadraat (R 2 ) het deel van de variantie in deresponsvariabele dat kan worden verklaard door de voorspellende variabele in een regressiemodel.
We gebruiken de volgende formule om R kwadraat te berekenen:
R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
Het volgende stapsgewijze voorbeeld laat zien hoe u handmatig het R-kwadraat voor een bepaald regressiemodel kunt berekenen.
Stap 1: Maak een dataset
Laten we eerst een dataset maken:
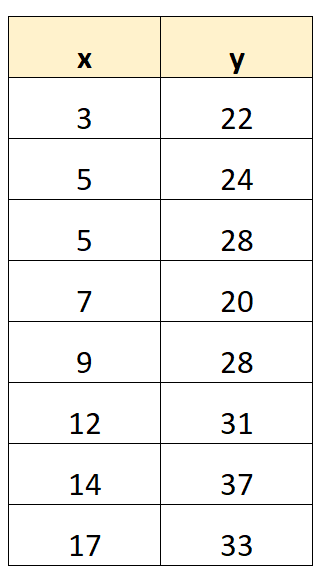
Stap 2: Bereken de benodigde statistieken
Laten we vervolgens elke metriek berekenen die we moeten gebruiken in de R2 -formule:
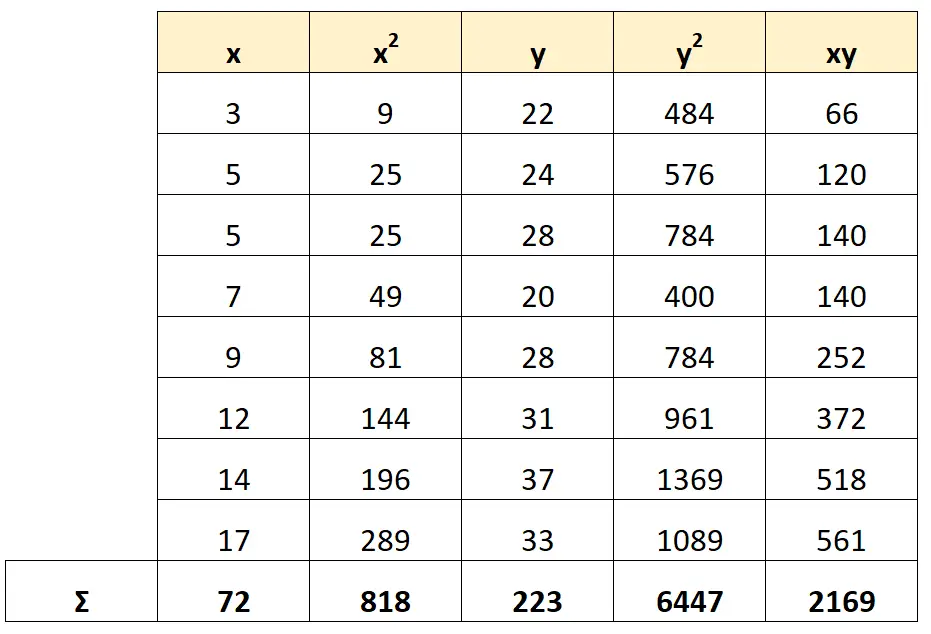
Stap 3: Bereken de R-kwadraat
Ten slotte zullen we elke metriek integreren in de formule voor R 2 :
- R 2 = [ (nΣxy – (Σx)(Σy)) / (√ nΣx 2 -(Σx) 2 * √ nΣy 2 -(Σy) 2 ) ] 2
- R 2 = [ (8*(2169) – (72)(223)) / (√ 8*(818)-(72) 2 * √ 8*(6447)-(223) 2 ) ] 2
- R2 = 0,6686
Opmerking: De n in de formule vertegenwoordigt het aantal waarnemingen in de dataset en blijkt in dit voorbeeld n = 8 waarnemingen te zijn.
Ervan uitgaande dat x de voorspellende variabele is en y de responsvariabele in dit regressiemodel, is de R-kwadraat van het model 0,6686 .
Dit vertelt ons dat 66,86% van de variatie in de variabele y kan worden verklaard door de variabele x .
Aanvullende bronnen
Inleiding tot eenvoudige lineaire regressie
Inleiding tot meervoudige lineaire regressie
R versus R-Square: wat is het verschil?
Wat is een goede R-kwadraatwaarde?
Über den Autor
Dr.benjamin anderson
Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder