Berkson-bias: definitie + voorbeelden

Berkson-bias is een soort bias die voorkomt in onderzoek wanneer twee variabelen negatief gecorreleerd lijken te zijn in de gegevens van een steekproef, maar in werkelijkheid positief gecorreleerd zijn in de totale populatie .

Stel bijvoorbeeld dat Tom de correlatie wil onderzoeken tussen de kwaliteit van hamburgers en milkshakes in lokale restaurants.

Het gaat uit en verzamelt de volgende gegevens over zeven verschillende restaurants:

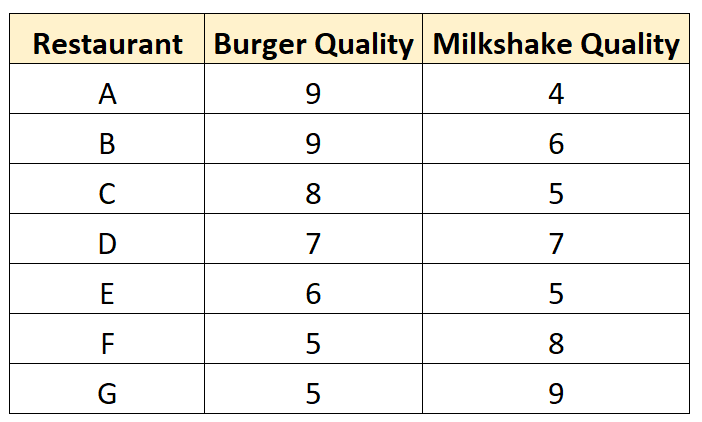
Er wordt een spreidingsdiagram gemaakt om de gegevens te visualiseren:

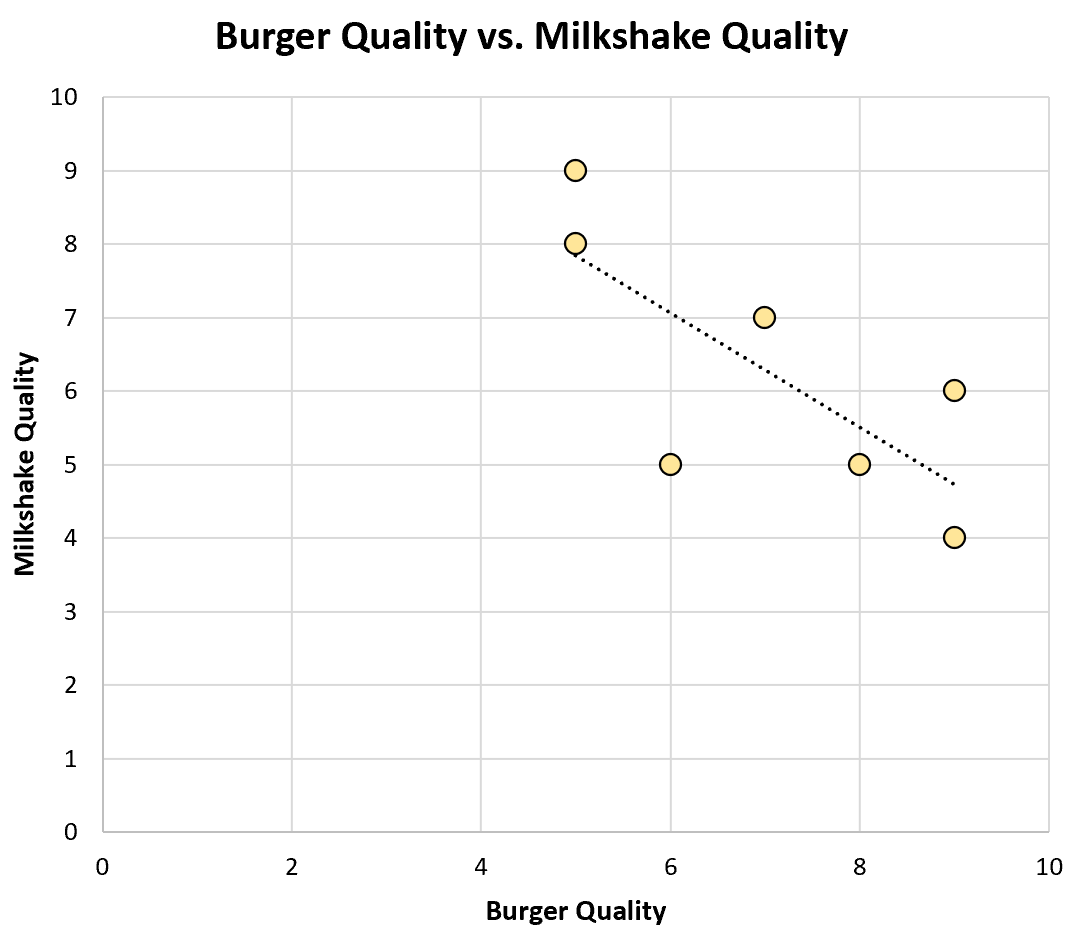
DePearson-correlatiecoëfficiënt tussen deze twee variabelen is -0,75 , wat overeenkomt met een sterke negatieve correlatie.

Deze ontdekking is contra-intuïtief voor Tom: hij zou denken dat restaurants die goede hamburgers maken, ook goede milkshakes maken.

Het blijkt echter dat Tom simpelweg alle restaurants in de stad heeft genegeerd die zowel slechte hamburgers als slechte milkshakes maken.

Als hij deze restaurants had bezocht, zou hij de volgende dataset hebben verzameld:

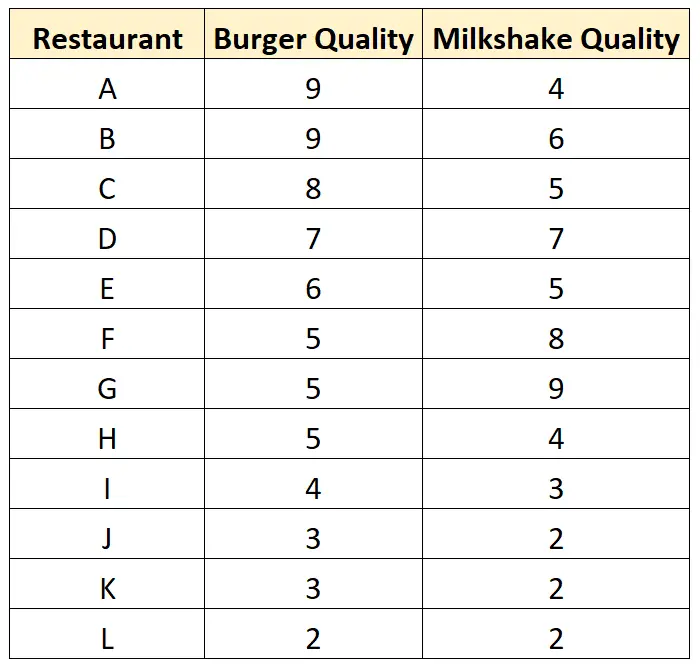
En zo ziet een spreidingsdiagram eruit voor deze dataset:

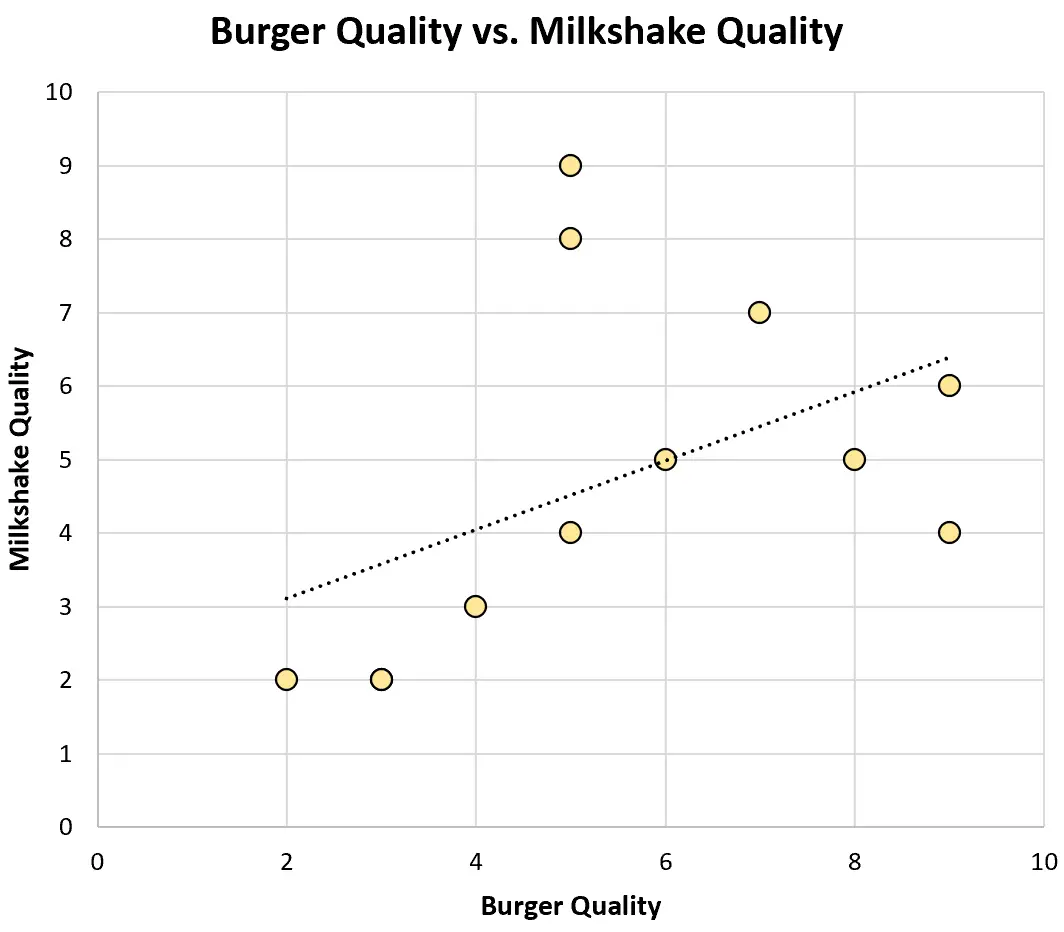
DePearson-correlatiecoëfficiënt tussen de twee variabelen blijkt 0,46 te zijn, wat een redelijk sterke positieve correlatie vertegenwoordigt.

Door slechts een deel van de restaurants in de stad te onderzoeken, concludeerde Tom ten onrechte dat er een negatieve correlatie bestond tussen de kwaliteit van hamburgers en milkshakes.

Het blijkt zelfs dat er een positieve relatie bestaat (zoals je zou verwachten) tussen deze twee variabelen. Dit is een klassiek voorbeeld van Berksons vooringenomenheid.

Zie de volgende voorbeelden voor andere scenario’s waarin Berkson-bias in de praktijk voorkomt.

Voorbeeld 1: toelating tot de universiteit

Stel dat een universiteit alleen studenten toelaat die een voldoende hoge GPA- en ACT-score hebben.

Het is algemeen bekend dat deze twee variabelen positief gecorreleerd zijn, maar het blijkt dat onder studenten die besluiten naar een bepaalde universiteit te gaan, er een negatieve correlatie tussen beide lijkt te bestaan.

Deze negatieve correlatie treedt echter alleen op omdat studenten met zowel een hoge GPA- als een ACT-score naar een elite-universiteit kunnen gaan, terwijl studenten met zowel een lage GPA- als een ACT-score helemaal niet worden toegelaten.

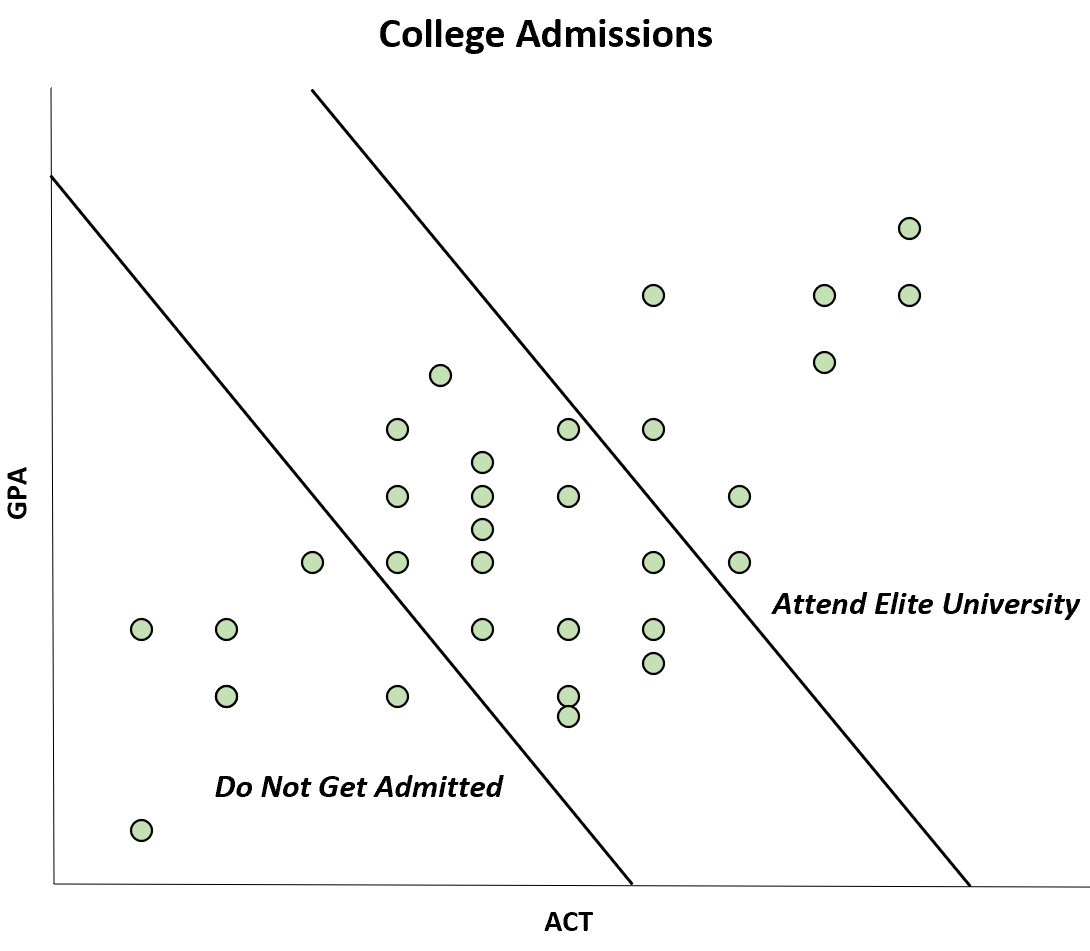
Hoewel de correlatie tussen ACT en GPA positief is in de populatie, lijkt de correlatie negatief in de steekproef. Dit is een geval van vooringenomenheid van de kant van Berkson.

Voorbeeld 2: Datingvoorkeuren

Veel mensen gaan alleen uit met partners die zowel aantrekkelijk zijn als een goede persoonlijkheid hebben.

In de echte wereld is er misschien geen correlatie tussen deze twee variabelen, maar als je de datingpool verkleint, kan een individu potentiële partners die zowel onaantrekkelijk als begaafd zijn, volledig negeren. ‚een goede persoonlijkheid.

Bij potentiële partners kan het er dus op lijken dat er een negatieve correlatie bestaat tussen deze twee variabelen: aantrekkelijkere mensen hebben slechtere persoonlijkheden, en mensen met betere persoonlijkheden lijken minder aantrekkelijk.

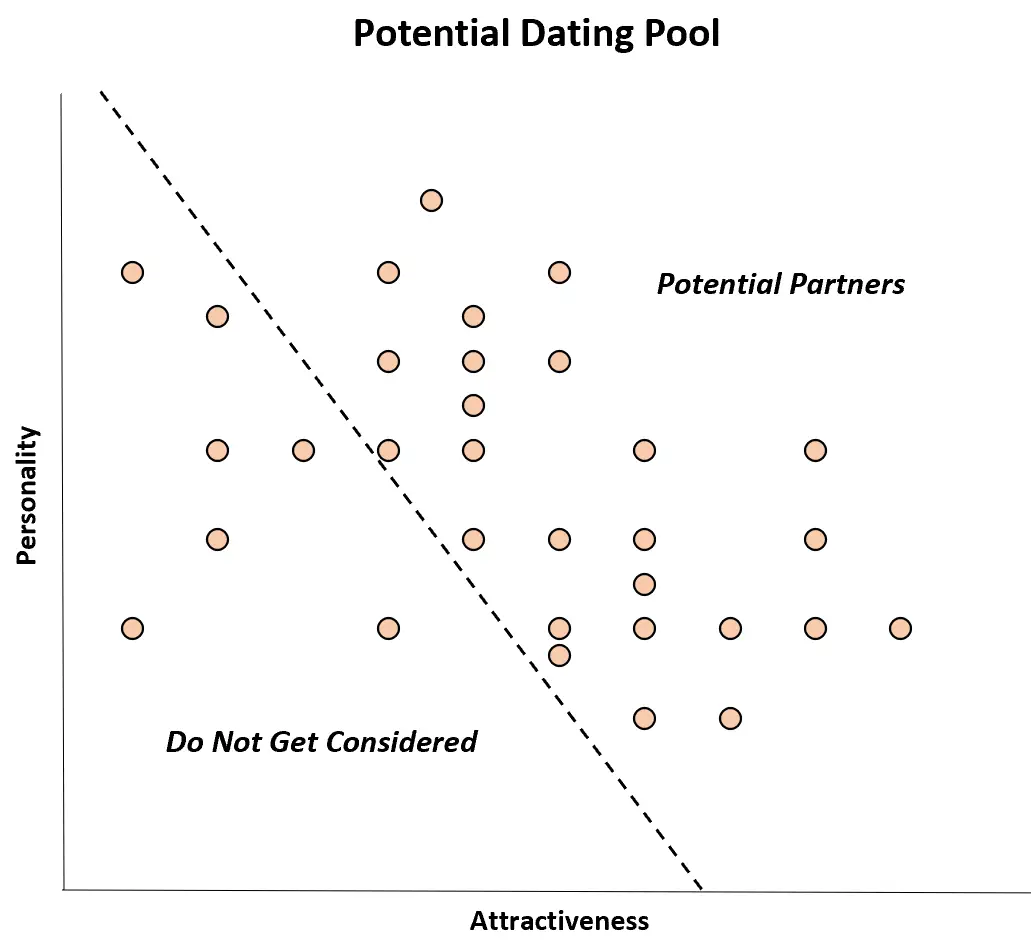
Hoewel er in de populatie geen correlatie bestaat tussen deze twee variabelen, lijkt er in de steekproef van potentiële partners wel een negatieve correlatie te bestaan. Dit is eenvoudigweg een geval van Berksons vooringenomenheid.

Hoe Berkson-vooroordelen te voorkomen

De meest voor de hand liggende manier om Berkson-vooroordelen in onderzoeksstudies te vermijden, is door een eenvoudige willekeurige steekproef uit een populatie te verzamelen. Met andere woorden, zorg ervoor dat elk lid van de populatie van interesse een gelijke kans heeft om in de steekproef te worden opgenomen.

Als u bijvoorbeeld de prevalentie van ziekten in een bepaald land bestudeert, moet u een steekproef verzamelen van personen uit het hele land, en niet alleen van degenen die gemakkelijk te bereiken zijn in ziekenhuizen.

Door een eenvoudige willekeurige steekproef te gebruiken, kunnen onderzoekers de kans maximaliseren dat hun steekproef representatief is voor de populatie, wat betekent dat ze met vertrouwen hun bevindingen uit de steekproef kunnen generaliseren naar de algehele populatie.