Bernoulli-verdeling en binominale verdeling: wat is het verschil?

Een willekeurige variabele volgt een Bernoulli-verdeling als deze slechts twee mogelijke uitkomsten heeft: 0 of 1.

Stel dat we één keer een munt opgooien. Laat blz . Dit betekent dat de kans dat de staart landt 1- p is.

We zouden dus kunnen schrijven:

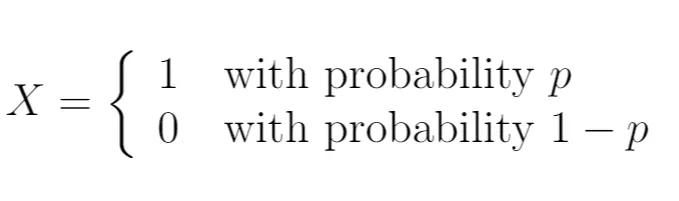
In dit geval volgt de willekeurige variabele X een Bernoulli-verdeling. Er kunnen slechts twee mogelijke waarden zijn.

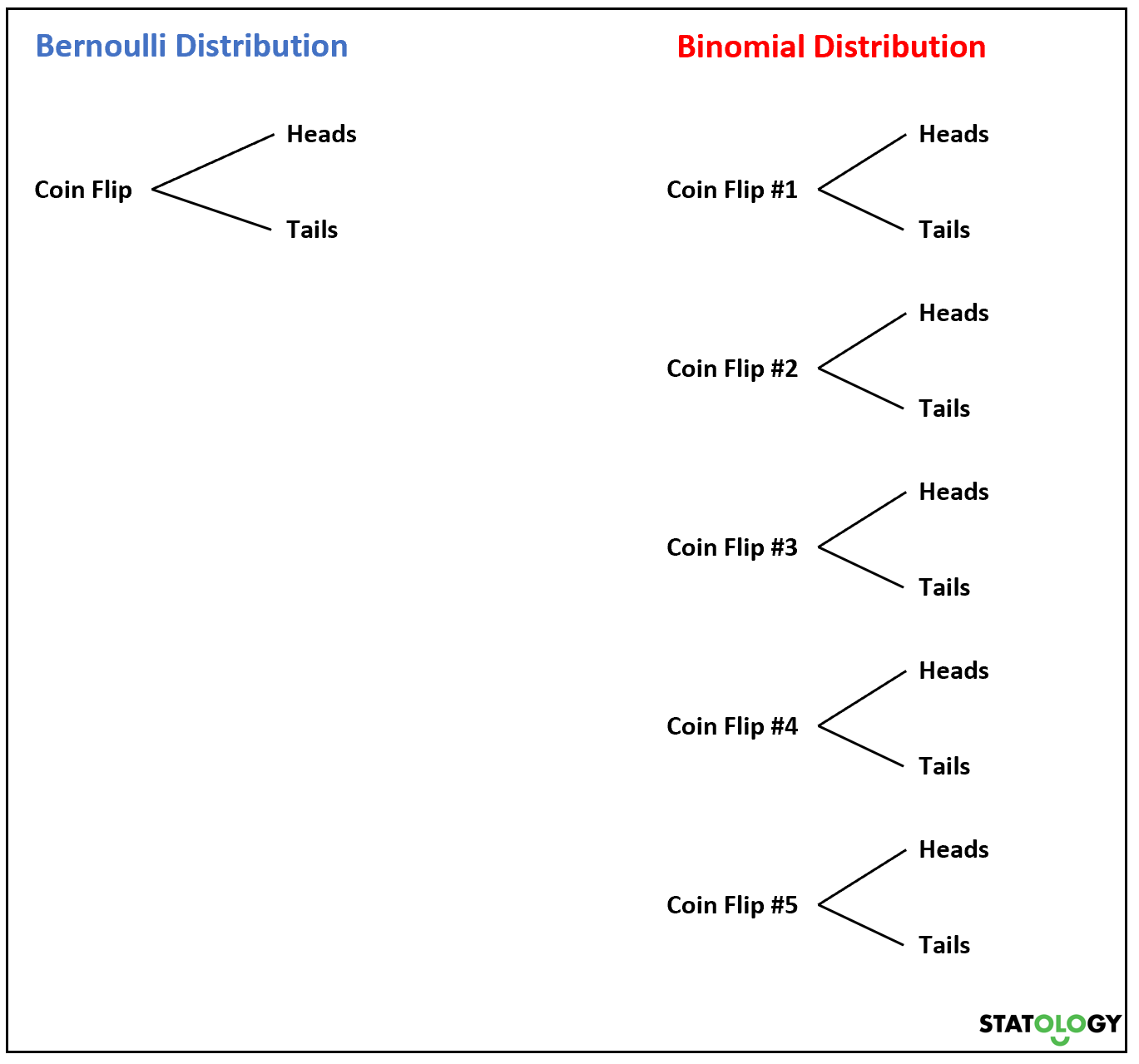
Als we nu een munt meerdere keren opgooien, zal de som van de Bernoulli-willekeurige variabelen een binominale verdeling volgen.

Stel dat we bijvoorbeeld vijf keer een munt opgooien en willen weten hoe groot de kans is dat we k keer kop krijgen. Het lijkt op de willekeurige variabele

Als een willekeurige variabele X een binominale verdeling volgt, kan de kans dat X = k succes wordt gevonden met de volgende formule:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Goud:

• n: aantal pogingen
• k: aantal successen
• p: kans op succes bij een bepaalde proef
• _n C _k : het aantal manieren om k successen te behalen in n pogingen

Stel dat we bijvoorbeeld drie keer een munt opgooien. We kunnen de bovenstaande formule gebruiken om de kans te bepalen op 0 kop tijdens deze 3 salto’s:

P(X=0) = ₃ C ₀ * 0,5 ⁰ * (1-0,5) ^3-0 = 1 * 1 * (0,5) ³ = 0,125

Wanneer n = 1 poging, is de binomiale verdeling equivalent aan de Bernoulli-verdeling.

Belangrijke aantekeningen

Hier zijn enkele belangrijke opmerkingen over de Bernoulli- en binominale verdeling:

1. Een willekeurige variabele die een Bernoulli-verdeling volgt, kan slechts twee mogelijke waarden aannemen, maar een willekeurige variabele die een binomiale verdeling volgt, kan meerdere waarden aannemen.

Bij een enkele toss hebben we bijvoorbeeld 0 of 1 kop. In een reeks van 5 trekkingen kunnen we echter 0, 1, 2, 3, 4 of 5 kop hebben.

2. Om een willekeurige variabele een binominale verdeling te laten volgen, moet de kans op „succes“ in elke Bernoulli-proef gelijk en onafhankelijk zijn.

Als we ’succes‘ bijvoorbeeld definiëren als landen met kop, dan is de kans op succes bij elke worp 0,5 en is elke worp onafhankelijk: de uitkomst van de ene worp heeft geen invloed op het resultaat van een andere.

Aanvullende bronnen

Een inleiding tot binominale experimenten
Een inleiding tot de binominale verdeling
De vorm van een binominale verdeling begrijpen