Beschrijvende of inferentiële statistiek: wat is het verschil?

Er zijn twee hoofdtakken op het gebied van statistiek:

• Beschrijvende statistieken
• Inferentiële statistieken

In deze tutorial wordt het verschil tussen de twee takken uitgelegd en waarom elk in bepaalde situaties nuttig is.

Beschrijvende statistieken

Kort gezegd heeft beschrijvende statistiek tot doel een reeks ruwe gegevens te beschrijven met behulp van samenvattende statistieken, grafieken en tabellen.

Beschrijvende statistieken zijn nuttig omdat u hiermee een groep gegevens veel sneller en gemakkelijker kunt begrijpen dan alleen maar naar rijen en rijen met onbewerkte gegevenswaarden te kijken.

Laten we bijvoorbeeld zeggen dat we een ruwe dataset hebben die de testscores toont van 1000 leerlingen op een bepaalde school. Mogelijk zijn we geïnteresseerd in de gemiddelde testscore en de verdeling van de testscores.

Met behulp van beschrijvende statistieken kunnen we de gemiddelde score vinden en een grafiek maken waarmee we de verdeling van de scores kunnen visualiseren.

Hierdoor kunnen we de toetsscores van studenten veel gemakkelijker begrijpen dan alleen naar de onbewerkte gegevens kijken.

Veel voorkomende vormen van beschrijvende statistiek

Er zijn drie veel voorkomende vormen van beschrijvende statistiek:

1. Samenvattende statistieken. Dit zijn statistieken die gegevens samenvatten in één getal. Er zijn twee veelvoorkomende typen samenvattende statistieken:

• Maatregelen voor centrale tendens : deze cijfers beschrijven waar het midden van een dataset zich bevindt. Voorbeelden hiervan zijn gemiddeld   en de mediaan .
• Verspreidingsmaten: Deze cijfers beschrijven de verdeling van waarden in de dataset. Voorbeelden zijn onder meer interval , interkwartielbereik , standaarddeviatie en variantie .

2. Grafische afbeeldingen . Grafieken helpen ons gegevens te visualiseren. Veelgebruikte typen diagrammen die worden gebruikt om gegevens te visualiseren zijn boxplots , histogrammen , stengel- en bladplots en spreidingsdiagrammen .

3. Tabellen . Tabellen kunnen ons helpen begrijpen hoe gegevens worden gedistribueerd. Een veelgebruikt type tabel is de frequentietabel , die ons vertelt hoeveel gegevenswaarden binnen bepaalde bereiken vallen.

Voorbeeld van het gebruik van beschrijvende statistieken

Het volgende voorbeeld illustreert hoe we beschrijvende statistieken in de echte wereld kunnen gebruiken.

Stel dat 1.000 leerlingen op een bepaalde school allemaal dezelfde test afleggen. We willen de verdeling van testresultaten begrijpen, daarom gebruiken we de volgende beschrijvende statistieken:

1. Samenvattende statistieken

Gemiddeld: 82,13 . Dit vertelt ons dat de gemiddelde toetsscore onder de 1.000 studenten 82,13 bedraagt.

Mediaan: 84. Dit vertelt ons dat de helft van alle studenten boven de 84 scoorde en de andere helft onder de 84.

Max: 100. Min: 45. Dit vertelt ons dat de maximale score die een student behaalde 100 was en de minimumscore 45. Het bereik – dat ons het verschil vertelt tussen het maximum en het minimum – is 55.

2. Afbeeldingen

Om de verdeling van de testresultaten te visualiseren, kunnen we een histogram maken: een soort diagram dat rechthoekige balken gebruikt om frequenties weer te geven.

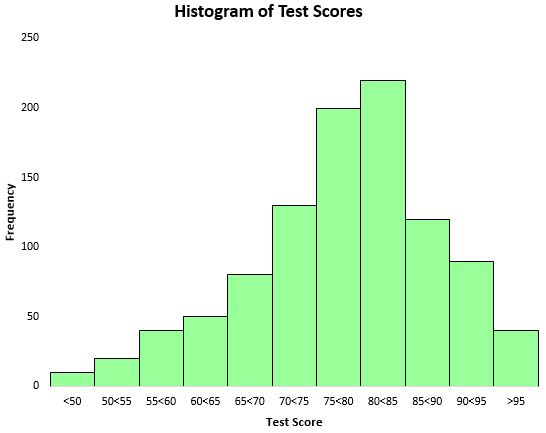
Op basis van dit histogram kunnen we zien dat de verdeling van de testscores grofweg klokvormig is. De meeste studenten scoorden tussen de 70 en 90, terwijl slechts weinigen boven de 95 scoorden en nog minder onder de 50.

3. Tabellen

Een andere eenvoudige manier om de verdeling van scores te begrijpen, is door een frequentietabel te maken. De volgende frequentietabel toont bijvoorbeeld het percentage studenten dat tussen verschillende bereiken scoorde:

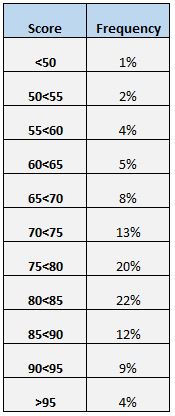
We kunnen zien dat slechts 4% van het totaal aantal studenten boven de 95 scoorde. We kunnen ook zien dat (12% + 9% + 4% = ) 25% van alle studenten een score van 85 of hoger scoorde.

Een frequentietabel is vooral handig als we willen weten welk percentage datawaarden boven of onder een bepaalde waarde ligt. Stel bijvoorbeeld dat de school een score boven de 75 als een ‘aanvaardbare’ toetsscore beschouwt.

Als we naar de frequentietabel kijken, kunnen we gemakkelijk zien dat (20% + 22% + 12% + 9% + 4% = ) 67% van de studenten een acceptabele score op de toets behaalde.

Inferentiële statistieken

Kortom, inferentiële statistiek gebruikt een kleine steekproef van gegevens om conclusies te trekken over de grotere populatie waaruit de steekproef is getrokken.

We willen bijvoorbeeld de politieke voorkeuren van miljoenen mensen in een land begrijpen.

Het zou echter te tijdrovend en te duur zijn om elk individu in het land te ondervragen. We zouden dus in plaats daarvan een kleiner onderzoek doen onder bijvoorbeeld 1.000 Amerikanen, en de onderzoeksresultaten gebruiken om conclusies te trekken over de bevolking als geheel.

Dit is het hele uitgangspunt van inferentiële statistiek: we willen een vraag over een populatie beantwoorden, dus we verkrijgen gegevens voor een kleine steekproef van die populatie en gebruiken de steekproefgegevens om conclusies te trekken over de populatie.

Het belang van een representatieve steekproef

Om vertrouwen te hebben in ons vermogen om een steekproef te gebruiken om conclusies te trekken over een populatie, moeten we ervoor zorgen dat we een representatieve steekproef hebben, dat wil zeggen een steekproef waarin de kenmerken van de individuen in de populatie aanwezig zijn. De steekproef komt nauw overeen met de steekproef kenmerken. van de totale bevolking.

Idealiter willen we dat onze steekproef lijkt op een ‘miniversie’ van onze populatie. Als we dus conclusies willen trekken over een studentenpopulatie die voor 50% uit meisjes en voor 50% uit jongens bestaat, zou onze steekproef niet representatief zijn als deze voor 90% uit jongens en slechts 10% uit meisjes zou bestaan.

Als onze steekproef niet vergelijkbaar is met de totale populatie, kunnen we de resultaten van de steekproef niet met zekerheid generaliseren naar de algehele populatie.

Hoe u een representatief monster kunt verkrijgen

Om de kansen op het verkrijgen van een representatieve steekproef te maximaliseren, moet u zich op twee dingen concentreren:

1. Zorg ervoor dat u een willekeurige steekproefmethode gebruikt.

Er zijn verschillende willekeurige steekproefmethoden die u kunt gebruiken en die waarschijnlijk een representatieve steekproef zullen opleveren, waaronder:

• Een eenvoudig willekeurig voorbeeld
• Een systematische willekeurige steekproef
• Een cluster willekeurige steekproef
• Een gestratificeerde willekeurige steekproef

Willekeurige steekproefmethoden leveren doorgaans representatieve steekproeven op, omdat elk lid van de populatie een gelijke kans heeft om in de steekproef te worden opgenomen.

2. Zorg ervoor dat uw steekproefgrootte groot genoeg is .

Naast het gebruik van een geschikte steekproefmethode is het belangrijk om ervoor te zorgen dat de steekproef groot genoeg is, zodat u over voldoende gegevens beschikt om te kunnen generaliseren naar een grotere populatie.

Om uw steekproefomvang te bepalen, moet u rekening houden met de omvang van de populatie die u bestudeert, het betrouwbaarheidsniveau dat u wilt gebruiken en de foutmarge die u acceptabel acht.

Gelukkig kun je online rekenmachines gebruiken om deze waarden in te voeren en te zien hoe groot je steekproefomvang moet zijn.

Veel voorkomende vormen van inferentiële statistieken

Er zijn drie veel voorkomende vormen van inferentiële statistieken:

1. Hypothesetesten.

We willen vaak vragen over een populatie beantwoorden, zoals:

• Is het percentage mensen in Ohio dat kandidaat A steunt groter dan 50%?
• Is de gemiddelde hoogte van een bepaalde plant gelijk aan 14 inch?
• Is er een verschil tussen de gemiddelde lengte van leerlingen op school A en school B?

Om deze vragen te beantwoorden, kunnen we hypothesetesten uitvoeren, waardoor we gegevens uit een steekproef kunnen gebruiken om conclusies te trekken over populaties.

2. Betrouwbaarheidsintervallen .

Soms willen we een bepaalde waarde schatten voor een populatie. We zijn bijvoorbeeld misschien geïnteresseerd in de gemiddelde hoogte van een bepaalde plantensoort in Australië.

In plaats van rond te gaan en elke plant in het land te meten, zouden we een klein monster van de planten kunnen verzamelen en ze allemaal kunnen meten. Vervolgens kunnen we de gemiddelde hoogte van de planten in het monster gebruiken om de gemiddelde lengte van de populatie te schatten.

Het is echter onwaarschijnlijk dat onze steekproef een perfecte populatieschatting zal opleveren. Gelukkig kunnen we rekening houden met deze onzekerheid door een betrouwbaarheidsinterval te creëren, dat een reeks waarden oplevert waarbinnen we er zeker van zijn dat de werkelijke populatieparameter ligt.

We zouden bijvoorbeeld een betrouwbaarheidsinterval van 95% van [13,2, 14,8] kunnen opleveren, wat betekent dat we er 95% zeker van zijn dat de werkelijke gemiddelde hoogte van deze plantensoort tussen 13,2 inch en 14,8 inch ligt.

3. Regressie .

Soms willen we de relatie tussen twee variabelen in een populatie begrijpen.

Laten we bijvoorbeeld zeggen dat we willen weten of de uren die we per week aan studeren verband houden met toetsscores . Om deze vraag te beantwoorden, zouden we een techniek kunnen uitvoeren die bekend staat alsregressieanalyse .

We kunnen dus zowel naar het aantal bestudeerde uren als naar de toetsscores van 100 studenten kijken en een regressieanalyse uitvoeren om te zien of er een significante relatie tussen de twee variabelen bestaat.

Als de p-waarde van de regressie significant blijkt te zijn , kunnen we concluderen dat er een significante relatie bestaat tussen deze twee variabelen in de totale studentenpopulatie.

Het verschil tussen beschrijvende en inferentiële statistieken

Samenvattend kan het verschil tussen beschrijvende en inferentiële statistieken als volgt worden beschreven:

Beschrijvende statistiek maakt gebruik van samenvattende statistieken, grafieken en tabellen om een reeks gegevens te beschrijven .

Dit is handig om ons te helpen een reeks gegevens snel en gemakkelijk te begrijpen zonder alle individuele gegevenswaarden te doorlopen.

Inferentiële statistieken gebruiken steekproeven om conclusies te trekken over grotere populaties.

Afhankelijk van de vraag die u over een populatie wilt beantwoorden, kunt u besluiten een of meer van de volgende methoden te gebruiken: het testen van hypothesen, betrouwbaarheidsintervallen en regressieanalyse.

Als u ervoor kiest een van deze methoden te gebruiken, houd er dan rekening mee dat uw steekproef representatief moet zijn voor uw populatie , anders zijn de conclusies die u trekt niet betrouwbaar.