Wat is een bètaniveau in statistieken? (definitie & #038; voorbeeld)

In de statistiek gebruiken we hypothesetoetsen om te bepalen of een hypothese over een populatieparameter waar is.

Een hypothesetest heeft altijd de volgende twee hypothesen:

Nulhypothese (H ₀ ): De steekproefgegevens komen overeen met de dominante overtuiging met betrekking tot de populatieparameter.

Alternatieve hypothese ( _HA ): De steekproefgegevens suggereren dat de hypothese in de nulhypothese niet waar is. Met andere woorden: een niet-willekeurige oorzaak beïnvloedt de gegevens.

Wanneer we een hypothesetest uitvoeren, zijn er altijd vier mogelijke uitkomsten:

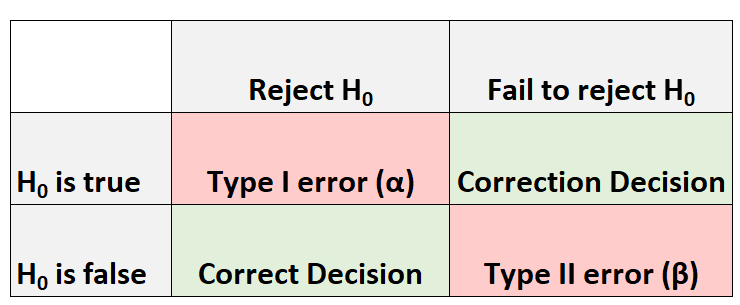
Er zijn twee soorten fouten die we kunnen maken:

• Type I-fout: we verwerpen de nulhypothese terwijl deze feitelijk waar is. De waarschijnlijkheid van dit type fout wordt aangegeven met α .
• Type II-fout: we slagen er niet in de nulhypothese te verwerpen terwijl deze feitelijk onwaar is. De waarschijnlijkheid van dit type fout wordt genoteerd als β .

De relatie tussen alfa en bèta

Idealiter willen onderzoekers dat de kans op het maken van een type I-fout en de kans op het maken van een type II-fout laag zijn.

Er bestaat echter een compromis tussen deze twee waarschijnlijkheden. Als we het alfaniveau verlagen, verkleinen we misschien de kans dat we een nulhypothese verwerpen terwijl deze feitelijk waar is, maar dit verhoogt in feite het bètaniveau – de kans dat we er niet in slagen de nulhypothese te verwerpen als deze verkeerd is.

De relatie tussen kracht en bèta

De kracht van een hypothesetest verwijst naar de waarschijnlijkheid dat een effect of verschil wordt gedetecteerd wanneer een effect of verschil daadwerkelijk aanwezig is. Met andere woorden, het is de waarschijnlijkheid dat een valse nulhypothese correct wordt verworpen.

Het wordt als volgt berekend:

Vermogen = 1 – β

Over het algemeen willen onderzoekers dat de kracht van een test hoog is, zodat als er een effect of verschil is, de test dit kan detecteren.

Uit de bovenstaande vergelijking kunnen we zien dat de beste manier om de kracht van een test te vergroten, is door het bètaniveau te verlagen. En de beste manier om het bètaniveau te verlagen is meestal door de steekproefomvang te vergroten.

De volgende voorbeelden laten zien hoe u het bètaniveau van een hypothesetest kunt berekenen en laten zien waarom het vergroten van de steekproefomvang het bètaniveau kan verlagen.

Voorbeeld 1: Bereken de bèta voor een hypothesetest

Stel dat een onderzoeker wil testen of het gemiddelde gewicht van in een fabriek geproduceerde widgets minder dan 500 gram bedraagt. We weten dat de standaardafwijking van de gewichten 24 ounces is en de onderzoeker besluit een willekeurige steekproef van 40 widgets te verzamelen.

Het zal de volgende hypothese realiseren bij α = 0,05:

• H ₀ : µ = 500
• H _A : μ < 500

Stel je nu voor dat het gemiddelde gewicht van de geproduceerde widgets feitelijk 490 gram is. Met andere woorden: de nulhypothese moet verworpen worden.

We kunnen de volgende stappen gebruiken om het bètaniveau te berekenen – de waarschijnlijkheid dat de nulhypothese niet wordt verworpen terwijl deze in feite zou moeten worden verworpen:

Stap 1: Zoek het gebied zonder afwijzing.

Volgens de kritische Z-waardecalculator is de linker kritische waarde bij α = 0,05 -1,645 .

Stap 2: Vind het minimale monster dat we niet kunnen afwijzen.

De teststatistiek wordt berekend als z = ( x – μ) / (s/ √n )

We kunnen dus deze vergelijking voor het steekproefgemiddelde oplossen:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/ √40 )
• x = 493,758

Stap 3: Bepaal de waarschijnlijkheid dat het minimale steekproefgemiddelde daadwerkelijk zal voorkomen.

Deze kans kunnen we als volgt berekenen:

• P(Z ≥ (493,758 – 490) / (24/√ 40 ))
• P(Z ≥ 0,99)

Volgens de normale CDF-calculator is de kans dat Z ≥ 0,99 0,1611 .

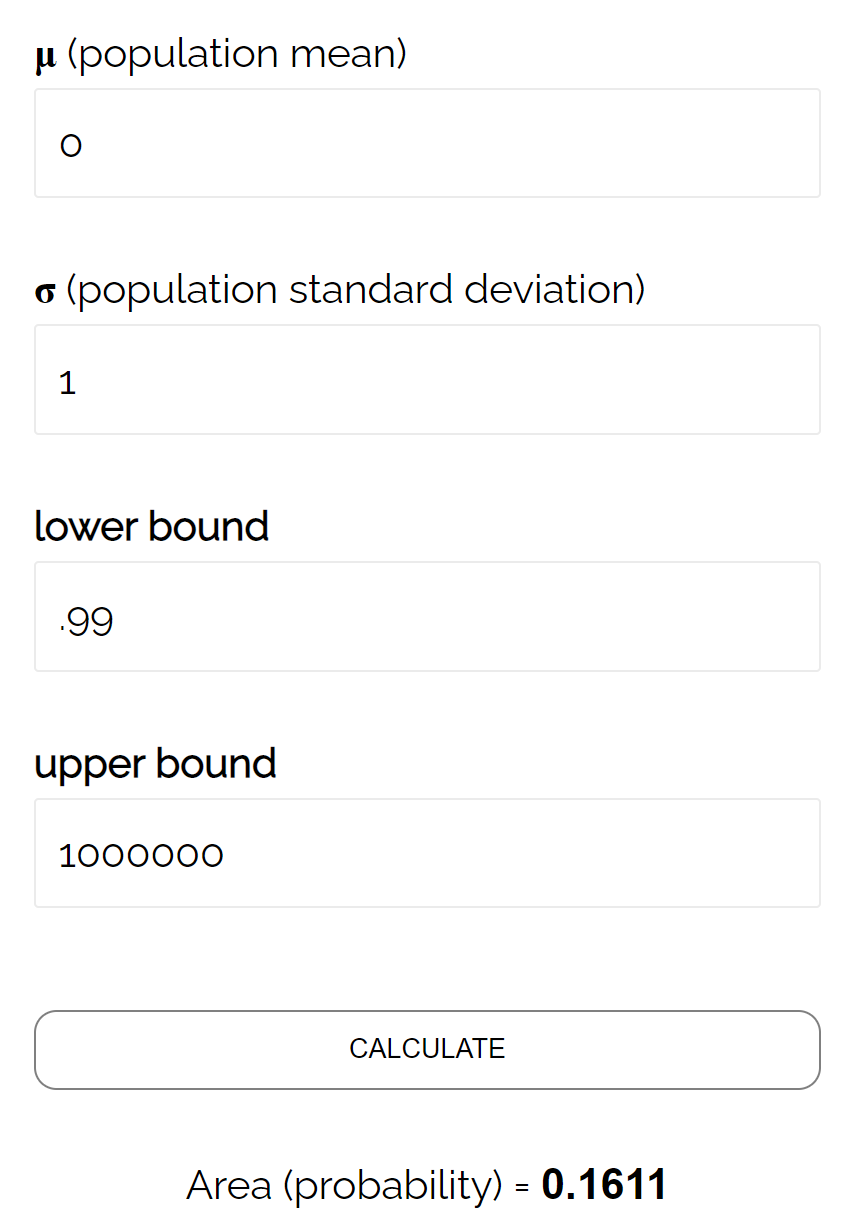
Het bètaniveau voor deze test is dus β = 0,1611. Dit betekent dat er een kans van 16,11% is dat het verschil niet wordt opgemerkt als het werkelijke gemiddelde 490 ounces is.

Voorbeeld 2: Bereken de bèta voor een test met een grotere steekproefomvang

Stel nu dat de onderzoeker exact dezelfde hypothesetest uitvoert, maar in plaats daarvan een steekproef van n = 100 widgets gebruikt. We kunnen dezelfde drie stappen herhalen om het bètaniveau voor deze test te berekenen:

Stap 1: Zoek het gebied zonder afwijzing.

Volgens de kritische Z-waardecalculator is de linker kritische waarde bij α = 0,05 -1,645 .

Stap 2: Vind het minimale monster dat we niet kunnen afwijzen.

De teststatistiek wordt berekend als z = ( x – μ) / (s/ √n )

We kunnen dus deze vergelijking voor het steekproefgemiddelde oplossen:

• x = µ – z*(s/ √n )
• x = 500 – 1,645*(24/√ 100 )
• x = 496,05

Stap 3: Bepaal de waarschijnlijkheid dat het minimale steekproefgemiddelde daadwerkelijk zal voorkomen.

Deze kans kunnen we als volgt berekenen:

• P(Z ≥ (496,05 – 490) / (24/√ 100 ))
• P(Z ≥ 2,52)

Volgens de normale CDF-calculator is de kans dat Z ≥ 2,52 0,0059.

Het bètaniveau voor deze test is dus β = 0,0059. Dit betekent dat er slechts een kans van 0,59% is dat het verschil niet wordt opgemerkt als het werkelijke gemiddelde 490 ounces is.

Merk op dat door simpelweg de steekproefomvang te vergroten van 40 naar 100, de onderzoeker het bètaniveau kon verlagen van 0,1611 naar 0,0059.

Bonus: gebruik deze Type II-foutcalculator om automatisch het bètaniveau van een test te berekenen.

Aanvullende bronnen

Inleiding tot het testen van hypothesen
Een nulhypothese schrijven (5 voorbeelden)
Een uitleg van P-waarden en statistische significantie