Een betrouwbaarheidsinterval creëren met behulp van de f-verdeling

Om te bepalen of de varianties van twee populaties gelijk zijn, kunnen we de variantieverhouding σ ² ₁ / σ ² ₂ berekenen, waarbij σ ² ₁ de variantie van populatie 1 is en σ ² ₂ de variantie van populatie 2.

Om de werkelijke populatievariantieverhouding te schatten, nemen we doorgaans een eenvoudige willekeurige steekproef uit elke populatie en berekenen we de steekproefvariantieverhouding, s ₁ ² / s ₂ ² , waarbij s ₁ ² en s ₂ ² de steekproefvarianties zijn voor steekproef 1 en steekproef . 2, respectievelijk.

Deze test gaat ervan uit dat s ₁ ² en s ₂ ² worden berekend op basis van onafhankelijke steekproeven met de grootte n ₁ en n ₂ , beide uit normaal verdeelde populaties.

Hoe verder deze verhouding van één verwijderd is, hoe sterker het bewijs van ongelijke varianties binnen de populatie.

Het (1-α)100% betrouwbaarheidsinterval voor σ ² ₁ / σ ² ₂ wordt gedefinieerd als:

(s ₁ ² / s ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n 2 -1, n 1 -1, a/2}

waarbij F _{n 2 -1, n 1 -1, α/2} en F _{n 1 -1, n 2 -1, α/2}   zijn de kritische waarden van de verdeling F voor het gekozen significantieniveau α.

De volgende voorbeelden illustreren hoe u een betrouwbaarheidsinterval voor σ ² ₁ / σ ² ₂ kunt maken met behulp van drie verschillende methoden:

• Bij de hand
• Gebruik Microsoft Excel
• Gebruik van R- statistische software

Voor elk van de volgende voorbeelden gebruiken we de volgende informatie:

• α = 0,05
• _n1 = 16
• _n2 = 11
• _s1 ² =28,2
• _s2 ² = 19,3

Handmatig een betrouwbaarheidsinterval creëren

Om handmatig een betrouwbaarheidsinterval voor σ ² ₁ / σ ² ₂ te berekenen, vullen we eenvoudigweg de getallen die we hebben in de formule voor het betrouwbaarheidsinterval in:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

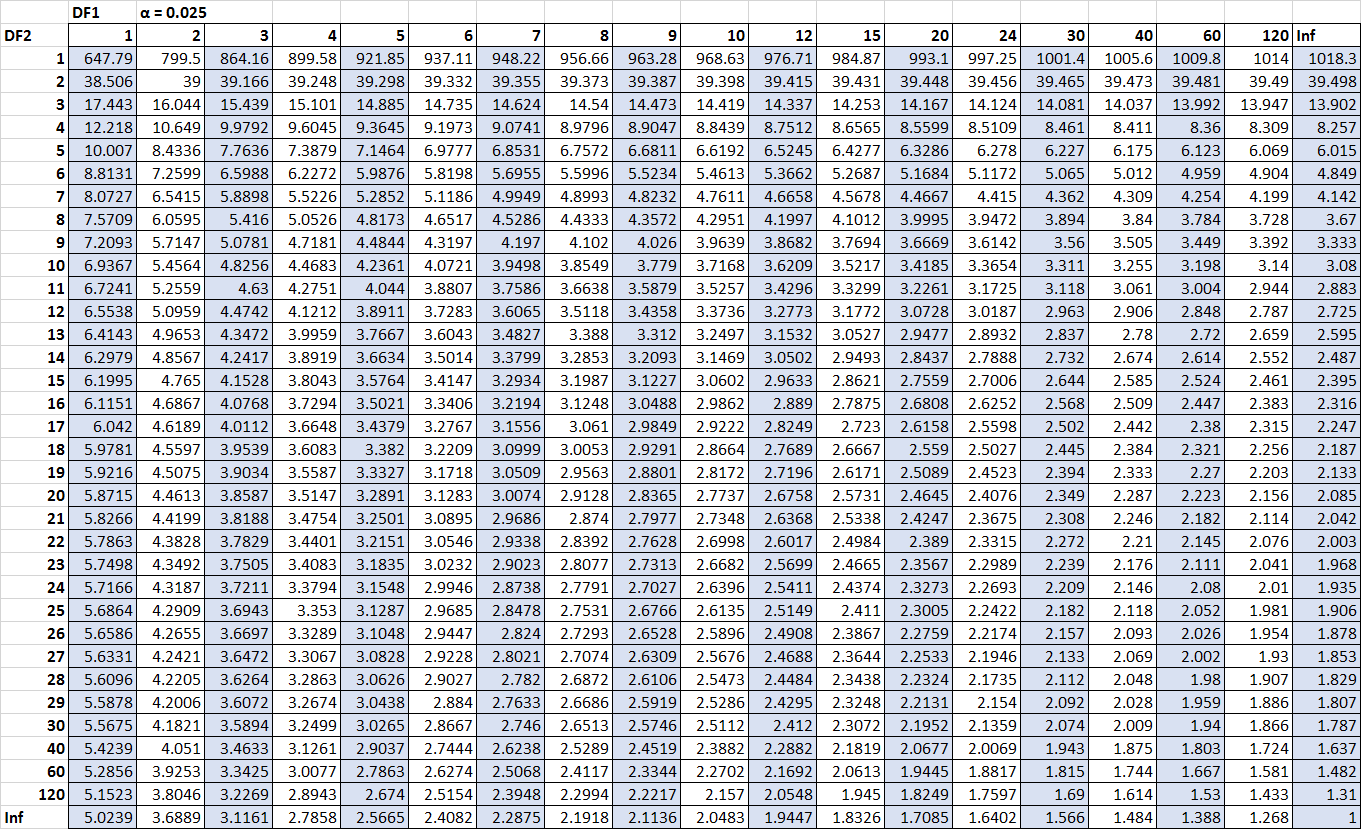
De enige cijfers die we missen zijn de kritische waarden. Gelukkig kunnen we deze kritische waarden terugvinden in de verdelingstabel F :

F _{n2-1, n1-1, α/2} = F _{10, 15, 0,025} = 3,0602

F _{n1-1, n2-1, α/2} = 1/ F _{15, 10, 0,025} = 1 / 3,5217 = 0,2839

(Klik om in te zoomen op de tafel)

We kunnen nu alle getallen in het betrouwbaarheidsformule-interval pluggen:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

(28,2 / 19,3) * (0,2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28,2 / 19,3) * (3,0602)

0,4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4,4714

Het 95% betrouwbaarheidsinterval voor de verhouding van populatievarianties is dus (0,4148; 4,4714) .

Een betrouwbaarheidsinterval creëren met Excel

De volgende afbeelding laat zien hoe u een betrouwbaarheidsinterval van 95% berekent voor de populatievariantieverhouding in Excel. De onder- en bovengrenzen van het betrouwbaarheidsinterval worden weergegeven in kolom E en de formule die wordt gebruikt om de onder- en bovengrenzen te vinden, wordt weergegeven in kolom F:

Het 95% betrouwbaarheidsinterval voor de verhouding van populatievarianties is dus (0,4148; 4,4714) . Dit komt overeen met wat we kregen toen we het betrouwbaarheidsinterval handmatig berekenden.

Een betrouwbaarheidsinterval creëren met behulp van R

De volgende code illustreert hoe u een betrouwbaarheidsinterval van 95% berekent voor de verhouding van populatievarianties in R:

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

Het 95% betrouwbaarheidsinterval voor de verhouding van populatievarianties is dus (0,4148; 4,4714) . Dit komt overeen met wat we kregen toen we het betrouwbaarheidsinterval handmatig berekenden.

Aanvullende bronnen

Hoe het F-verdeelbord te lezen
Hoe de kritische waarde F in Excel te vinden