Hoe u betrouwbaarheidsintervallen in google spreadsheets kunt berekenen

Een betrouwbaarheidsinterval voor een gemiddelde is een reeks waarden die waarschijnlijk een populatiegemiddelde met een bepaald betrouwbaarheidsniveau bevatten.

Het wordt als volgt berekend:

Betrouwbaarheidsinterval = x +/- t*(s/√ n )

Goud:

• x : steekproefgemiddelde
• t: t-waarde die overeenkomt met het betrouwbaarheidsniveau
• s: standaardafwijking van het monster
• n: steekproefomvang

In deze zelfstudie wordt uitgelegd hoe u betrouwbaarheidsintervallen in Google Spreadsheets kunt berekenen.

Betrouwbaarheidsintervallen met behulp van de t-verdeling

Als we met een kleine steekproef werken (n < 30), kunnen we de t-verdeling gebruiken om een betrouwbaarheidsinterval voor een populatiegemiddelde te berekenen.

Stel dat we bijvoorbeeld een betrouwbaarheidsinterval willen berekenen voor de werkelijke gemiddelde populatiehoogte (in inches) van een bepaalde plantensoort, met behulp van een steekproef van 15 planten:

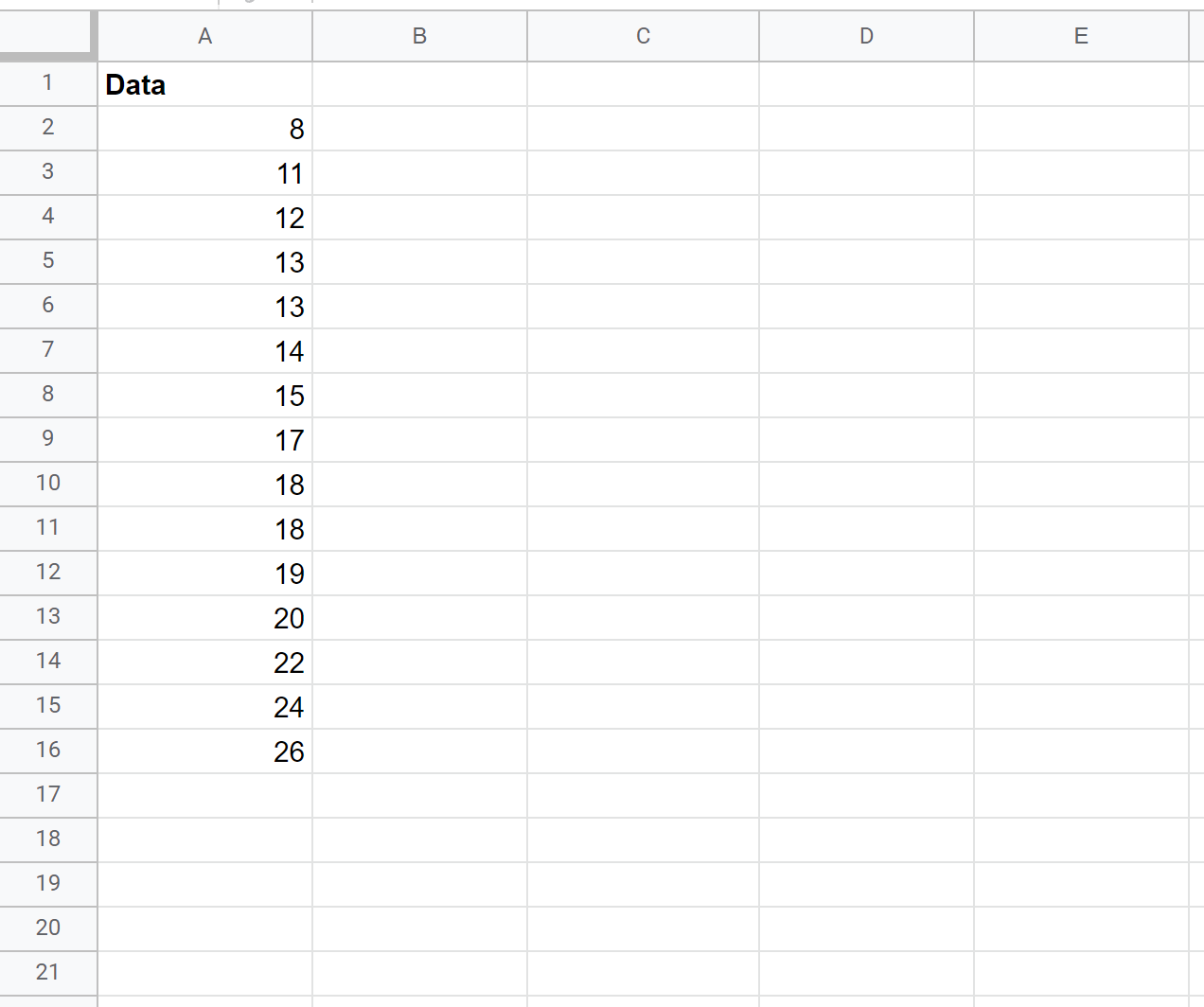
Ten eerste kunnen we het steekproefgemiddelde, de steekproefstandaarddeviatie en de steekproefomvang berekenen:

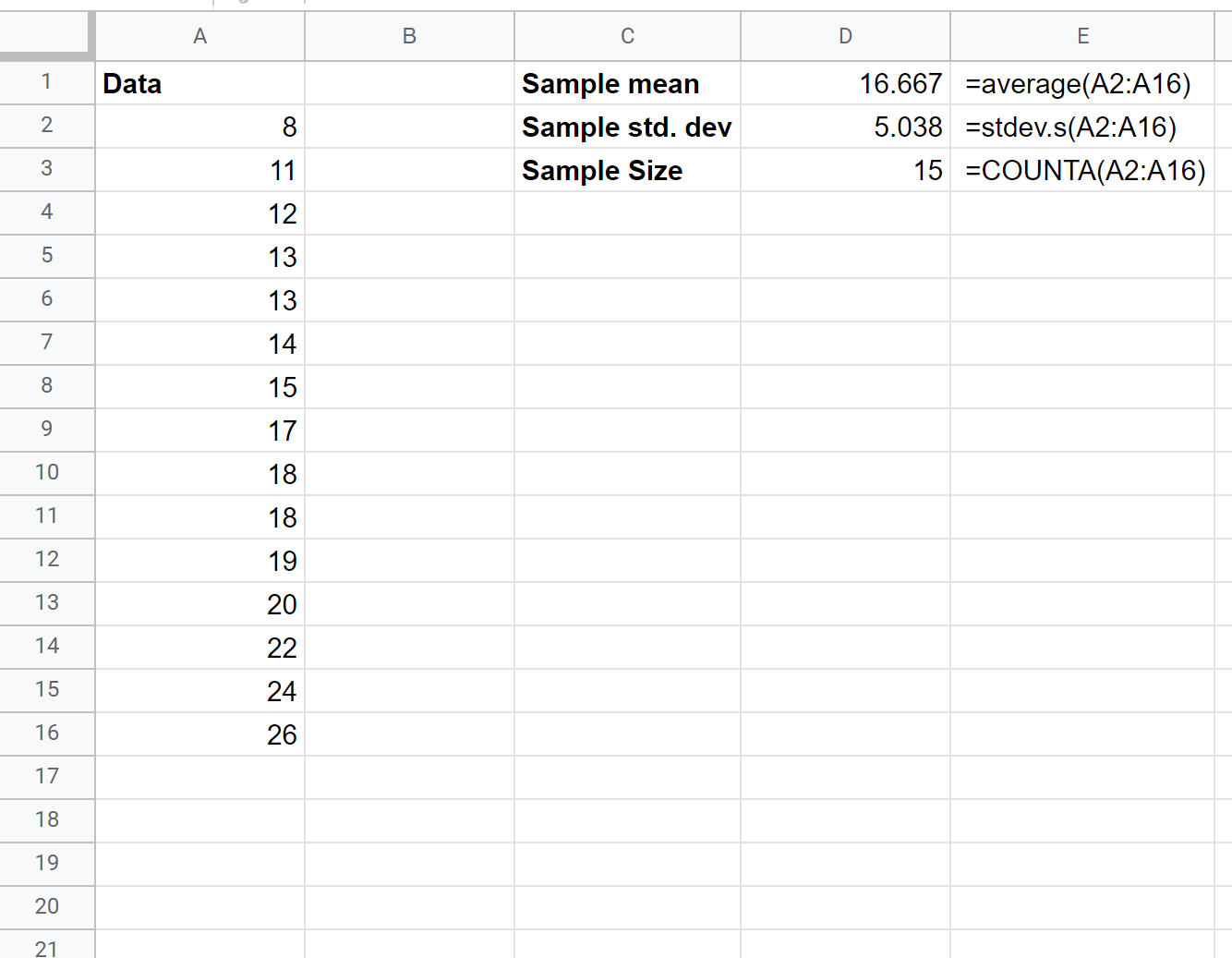
Vervolgens kunnen we de volgende formules gebruiken om de onder- en bovengrens van het 95%-betrouwbaarheidsinterval te berekenen:

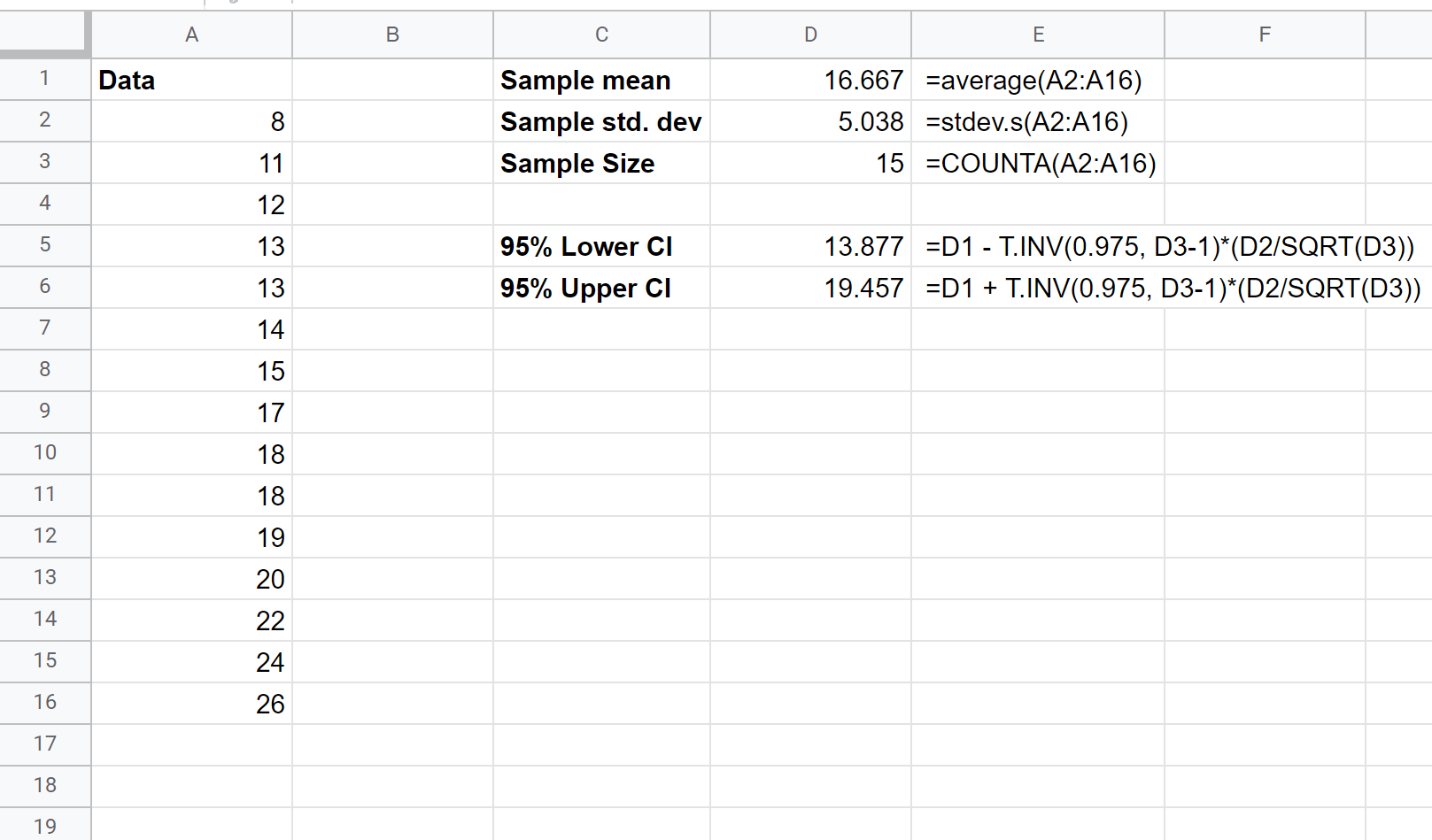
Het 95% betrouwbaarheidsinterval voor de werkelijke gemiddelde populatiegrootte is (13,877; 19,457) .

Betrouwbaarheidsintervallen met behulp van de normale verdeling

Als we met grotere steekproeven werken (n≥30), kunnen we aannemen dat de steekproefverdeling van het steekproefgemiddelde normaal verdeeld is dankzij de centrale limietstelling .

Dit betekent dat we in plaats daarvan de functie NORM.S.INV() kunnen gebruiken om de kritische waarde te berekenen die voor het betrouwbaarheidsinterval moet worden gebruikt.

Het volgende voorbeeld laat zien hoe u een betrouwbaarheidsinterval kunt berekenen voor de werkelijke gemiddelde populatiehoogte (in inches) van een bepaalde plantensoort, met behulp van een steekproef van 30 planten:

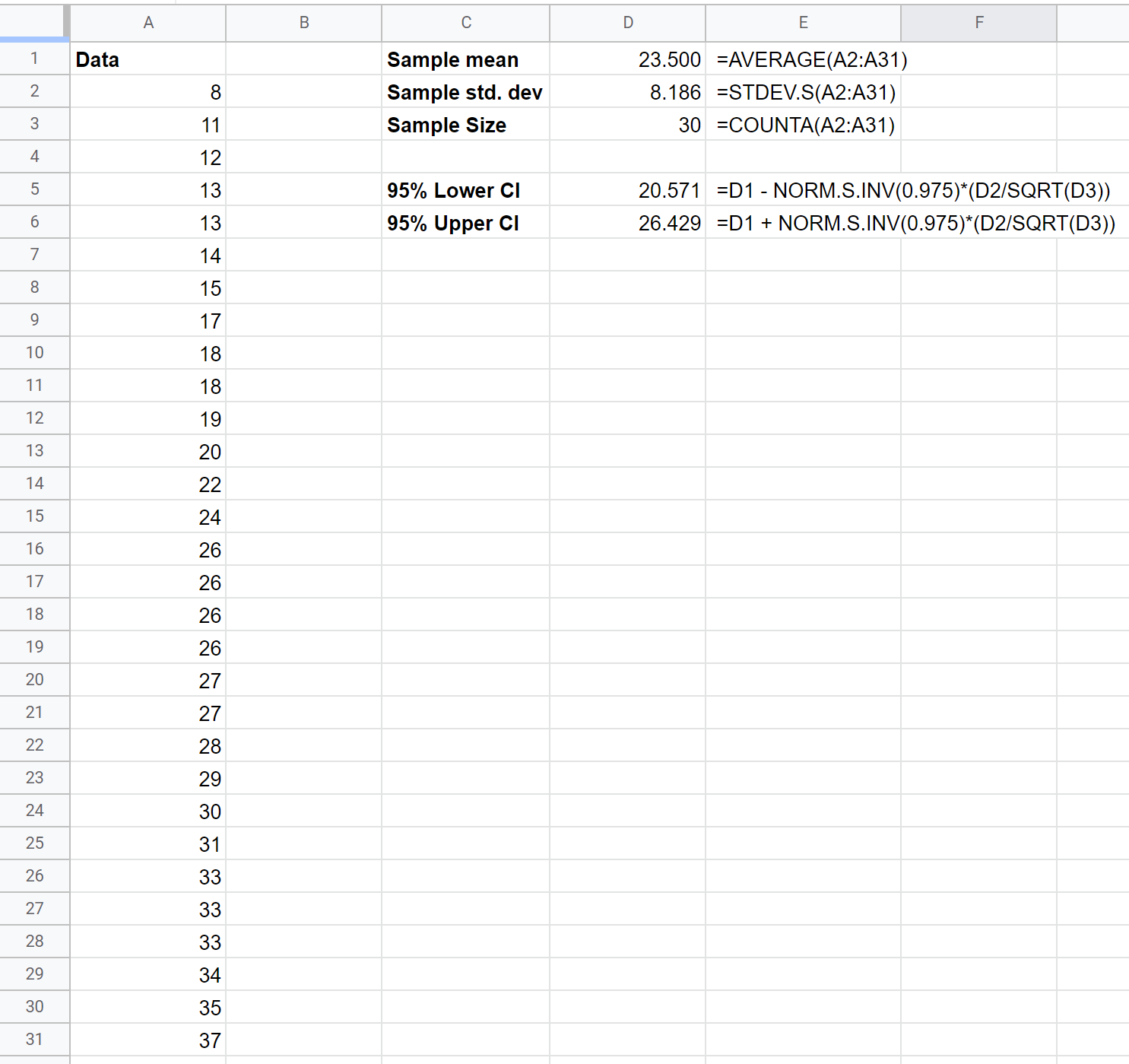
Het 95% betrouwbaarheidsinterval voor de werkelijke gemiddelde populatiegrootte is (20,571; 26,429) .

Merk op dat hogere betrouwbaarheidsniveaus leiden tot bredere betrouwbaarheidsintervallen. U kunt bijvoorbeeld als volgt een BI van 99% berekenen voor exact dezelfde gegevens:

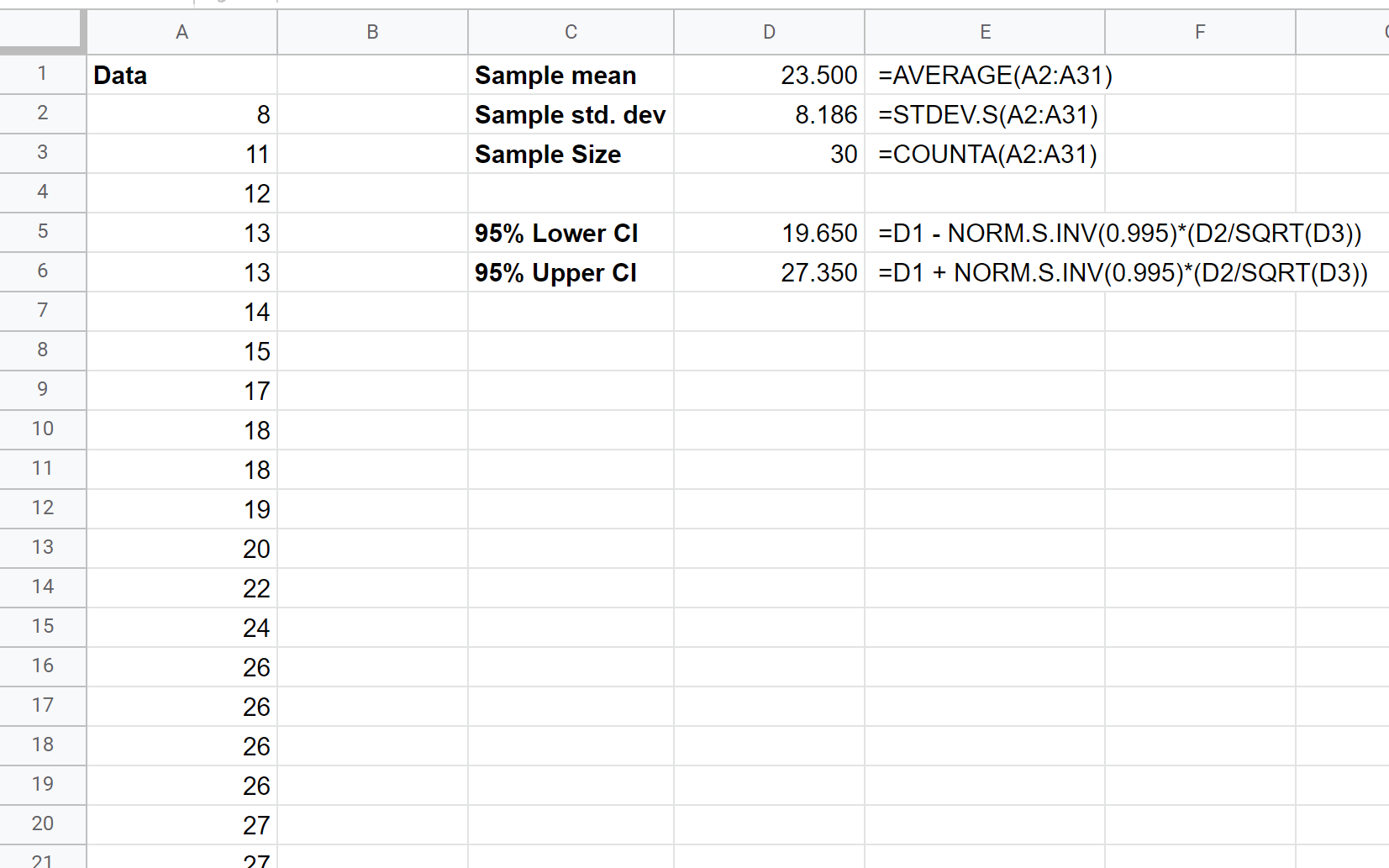
Het 99% betrouwbaarheidsinterval voor de werkelijke gemiddelde populatiegrootte is (19.650, 27.350) .

Merk op dat dit betrouwbaarheidsinterval van 99% breder is dan het betrouwbaarheidsinterval van 95% dat we eerder hebben berekend.

Gerelateerd: vertrouwensniveau vs. Betrouwbaarheidsinterval: wat is het verschil?

Aanvullende bronnen

In de volgende tutorials wordt uitgelegd hoe u betrouwbaarheidsintervallen kunt berekenen met behulp van andere statistische software:

Hoe betrouwbaarheidsintervallen in Excel te berekenen
Hoe betrouwbaarheidsintervallen in R te berekenen
Hoe betrouwbaarheidsintervallen in Python te berekenen