Betrouwbaarheidsinterval voor verschil tussen gemiddelden

Een betrouwbaarheidsinterval (CI) voor een verschil tussen gemiddelden is een reeks waarden die met een bepaald betrouwbaarheidsniveau waarschijnlijk het werkelijke verschil tussen twee populatiegemiddelden bevat.

In deze zelfstudie wordt het volgende uitgelegd:

• De motivatie om dit betrouwbaarheidsinterval te creëren.
• De formule om dit betrouwbaarheidsinterval te creëren.
• Een voorbeeld van hoe u dit betrouwbaarheidsinterval kunt berekenen.
• Hoe dit betrouwbaarheidsinterval te interpreteren.

CI voor het verschil tussen middelen: motivatie

Onderzoekers willen vaak het verschil schatten tussen de gemiddelden van twee populaties. Om dit verschil te schatten, verzamelen ze een willekeurige steekproef uit elke populatie en berekenen ze het gemiddelde voor elke steekproef. Vervolgens kunnen ze het verschil tussen de twee gemiddelden vergelijken.

Ze kunnen echter niet zeker weten of het verschil tussen de steekproefgemiddelden overeenkomt met het werkelijke verschil tussen de populatiegemiddelden. Daarom kunnen ze een betrouwbaarheidsinterval creëren voor het verschil tussen de twee gemiddelden. Dit levert een reeks waarden op die waarschijnlijk het werkelijke verschil tussen de populatiegemiddelden bevatten.

Stel dat we bijvoorbeeld het verschil in gemiddeld gewicht tussen twee verschillende soorten schildpadden willen schatten. Omdat er in elke populatie duizenden schildpadden zijn, zou het te tijdrovend en te duur zijn om elke schildpad afzonderlijk te wegen.

In plaats daarvan zouden we een eenvoudige willekeurige steekproef van 15 schildpadden uit elke populatie kunnen nemen en het gemiddelde gewicht van elke steekproef kunnen gebruiken om het werkelijke verschil in gemiddeld gewicht tussen de twee populaties te schatten:

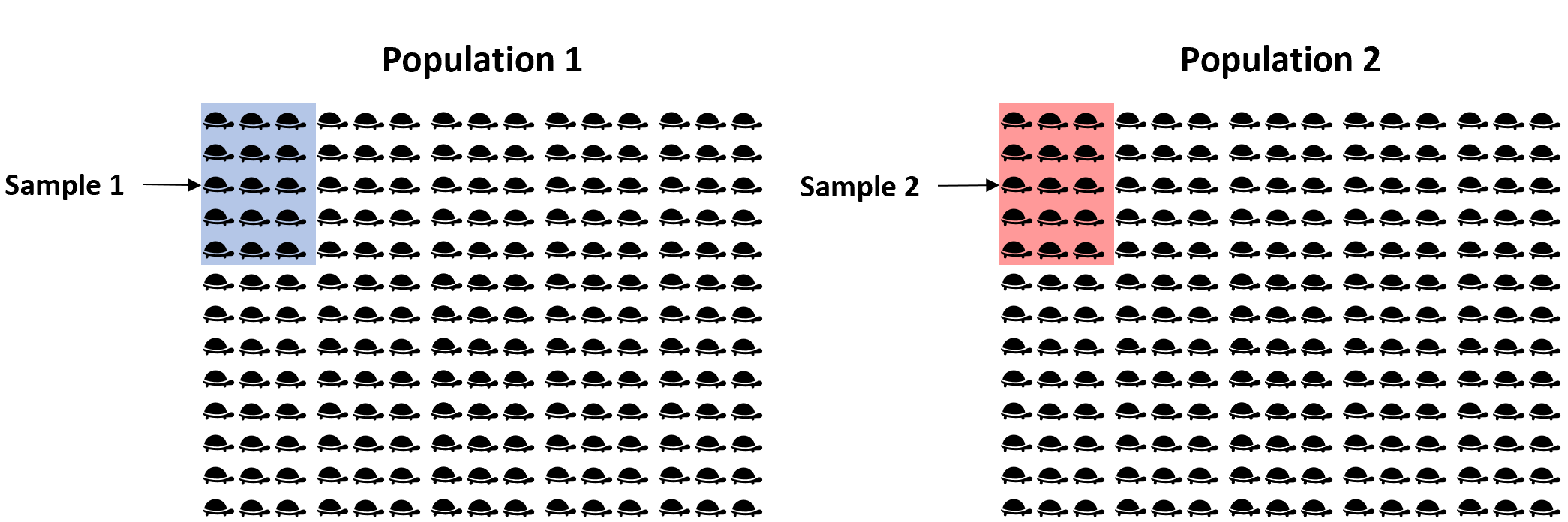
Het probleem is dat onze steekproeven willekeurig zijn. Het is dus niet gegarandeerd dat het verschil in gemiddeld gewicht tussen de twee steekproeven exact overeenkomt met het verschil in gemiddeld gewicht tussen de twee populaties. Om deze onzekerheid vast te leggen, kunnen we dus een betrouwbaarheidsinterval creëren dat een reeks waarden bevat die waarschijnlijk het werkelijke verschil in gemiddeld gewicht tussen de twee populaties zullen bevatten.

CI voor het verschil tussen middelen: formule

We gebruiken de volgende formule om een betrouwbaarheidsinterval te berekenen voor een verschil tussen twee gemiddelden:

Betrouwbaarheidsinterval = ( x ₁ – x ₂ ) +/- t*√((s _p ² /n ₁ ) + (s _p ² /n ₂ ))

Goud:

• x ₁ , x ₂ : gemiddelde van monster 1, gemiddelde van monster 2
• t: de t-kritische waarde gebaseerd op het betrouwbaarheidsniveau en (n ₁ + n ₂ -2) vrijheidsgraden
• s _p ² : gepoolde variantie
• n ₁ , n ₂ : steekproefomvang 1, steekproefomvang 2

Goud:

• De gepoolde variantie wordt als volgt berekend: s _p ² = ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² ) / (n ₁ +n ₂ -2)
• De t-kritische waarde t kan worden gevonden met behulp van de inverse t-verdelingscalculator.

CI voor het verschil tussen middelen: voorbeeld

Stel dat we het verschil in gemiddeld gewicht tussen twee verschillende soorten schildpadden willen schatten. We zullen daarom een willekeurige steekproef van 15 schildpadden uit elke populatie verzamelen. Hier volgen de samenvattende gegevens voor elk monster:

Voorbeeld 1:

• x1 = ₃₁₀
• _s1 = 18,5
• _n1 = 15

Voorbeeld 2:

• x2 ₌ 300
• _s2 = 16,4
• _n2 = 15

Zo vindt u verschillende betrouwbaarheidsintervallen voor het werkelijke verschil in populatiegemiddelde gewichten:

90% betrouwbaarheidsinterval:

(310-300) +/- 1,70*√((305,61/15) + (305,61/15)) = [-0,8589, 20,8589]

95% betrouwbaarheidsinterval:

(310-300) +/- 2,05*√((305,61/15) + (305,61/15)) = [-3,0757, 23,0757]

99% betrouwbaarheidsinterval:

(310-300) +/- 2,76*√((305,61/15) + (305,61/15)) = [-7,6389, 27,6389]

Opmerking: u kunt deze betrouwbaarheidsintervallen ook vinden met behulp van de Statistical Confidence Interval for Difference Between Means Calculator .

U zult merken dat hoe hoger het betrouwbaarheidsniveau, hoe breder het betrouwbaarheidsinterval. Dit zou logisch moeten zijn, omdat het waarschijnlijker is dat bredere intervallen het werkelijke populatiegemiddelde bevatten, zodat we er meer „vertrouwen“ in hebben dat het interval het werkelijke populatiegemiddelde bevat.

CI voor het verschil tussen middelen : interpretatie

De manier waarop we een betrouwbaarheidsinterval zouden interpreteren is:

Er is een kans van 95% dat het betrouwbaarheidsinterval van [-3,0757, 23,0757] het werkelijke verschil in gemiddeld gewicht tussen de twee schildpadpopulaties bevat.

Omdat dit interval de waarde „0“ bevat, betekent dit dat het mogelijk is dat er geen verschil in gemiddeld gewicht is tussen de schildpadden uit deze twee populaties. Met andere woorden: we kunnen niet met 95% zekerheid zeggen dat er een verschil is in het gemiddelde gewicht tussen schildpadden uit deze twee populaties.