Betrouwbaarheidsinterval voor verschil in verhoudingen
Een betrouwbaarheidsinterval (CI) voor een verschil in verhoudingen is een reeks waarden die met een bepaald niveau van vertrouwen waarschijnlijk het werkelijke verschil tussen twee populatieverhoudingen zal bevatten.
In deze zelfstudie wordt het volgende uitgelegd:
- De motivatie om dit betrouwbaarheidsinterval te creëren.
- De formule om dit betrouwbaarheidsinterval te creëren.
- Een voorbeeld van hoe u dit betrouwbaarheidsinterval kunt berekenen.
- Hoe dit betrouwbaarheidsinterval te interpreteren.
CI voor het verschil in verhoudingen: motivatie
Onderzoekers willen vaak het verschil tussen twee populatieverhoudingen schatten. Om dit verschil te schatten, verzamelen ze een willekeurige steekproef uit elke populatie en berekenen ze het aandeel voor elke steekproef. Vervolgens kunnen ze het verschil tussen de twee verhoudingen vergelijken.
Ze kunnen echter niet zeker weten of het verschil tussen de steekproefaandelen overeenkomt met het werkelijke verschil tussen de populatieaandelen. Dit is de reden waarom ze een betrouwbaarheidsinterval kunnen creëren voor het verschil tussen de twee verhoudingen. Dit levert een reeks waarden op die waarschijnlijk het werkelijke verschil tussen populatieverhoudingen bevatten.
Stel dat we bijvoorbeeld het verschil willen schatten tussen het aandeel inwoners dat een bepaalde wet in County A steunt, en het aandeel dat de wet in County B steunt.
Aangezien er in elke provincie duizenden inwoners zijn, zou het te tijdrovend en te duur zijn om elke individuele inwoner in elke provincie te onderzoeken.
In plaats daarvan zouden we een eenvoudige willekeurige steekproef van inwoners uit elke provincie kunnen nemen en het aandeel in het voordeel van de wet in elke steekproef kunnen gebruiken om het werkelijke verschil in verhoudingen tussen de twee provincies te schatten:
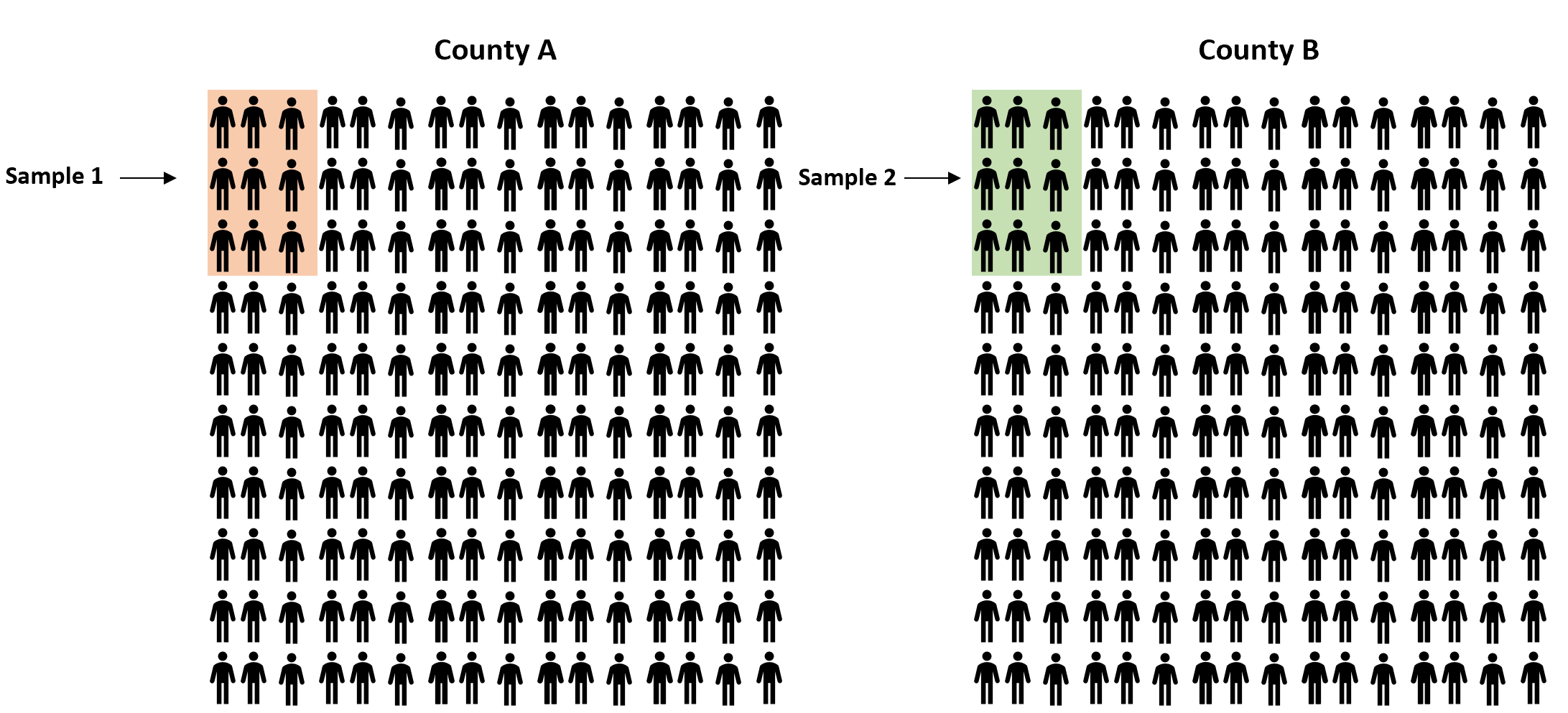
Omdat onze steekproeven willekeurig zijn, is het niet gegarandeerd dat het verschil in verhoudingen tussen de twee steekproeven exact overeenkomt met het verschil in verhoudingen tussen de twee populaties. Om deze onzekerheid vast te leggen, kunnen we dus een betrouwbaarheidsinterval creëren dat een reeks waarden bevat die waarschijnlijk het werkelijke verschil in verhoudingen tussen de twee populaties zullen bevatten.
CI voor het verschil in verhoudingen: formule
We gebruiken de volgende formule om een betrouwbaarheidsinterval te berekenen voor een verschil tussen twee populatieverhoudingen:
Betrouwbaarheidsinterval = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
Goud:
- p 1 , p 2 : aandeel van monster 1, aandeel van monster 2
- z: de z-kritische waarde gebaseerd op het betrouwbaarheidsniveau
- n 1 , n 2 : steekproefomvang 1, steekproefomvang 2
De z-waarde die u gebruikt, hangt af van het betrouwbaarheidsniveau dat u kiest. De volgende tabel toont de z-waarde die overeenkomt met de meest voorkomende keuzes op het gebied van het betrouwbaarheidsniveau:
| Een niveau van vertrouwen | z-waarde |
|---|---|
| 0,90 | 1.645 |
| 0,95 | 1,96 |
| 0,99 | 2.58 |
Merk op dat hogere betrouwbaarheidsniveaus overeenkomen met grotere z-waarden, wat leidt tot bredere betrouwbaarheidsintervallen. Dit betekent dat bijvoorbeeld een betrouwbaarheidsinterval van 95% breder zal zijn dan een betrouwbaarheidsinterval van 90% voor dezelfde gegevensset.
CI voor het verschil in verhoudingen: voorbeeld
Stel dat we het verschil willen schatten tussen het aandeel inwoners dat een bepaalde wet in County A steunt, vergeleken met het aandeel dat de wet in County B steunt. Hier zijn de samenvattende gegevens voor elke steekproef:
Voorbeeld 1:
- n1 = 100
- p 1 = 0,62 (dwz 62 van de 100 inwoners steunen de wet)
Voorbeeld 2:
- n2 = 100
- p 2 = 0,46 (dwz 46 van de 100 inwoners steunen de wet)
Zo vindt u verschillende betrouwbaarheidsintervallen voor het verschil in populatieverhoudingen:
90% betrouwbaarheidsinterval:
(.62-.46) +/- 1,645*√(.62(1-.62)/100 + .46(1-.46)/100) = [.0456, .2744]
95% betrouwbaarheidsinterval:
(.62-.46) +/- 1,96*√(.62(1-.62)/100 + .46(1-.46)/100) = [.0236, .2964]
99% betrouwbaarheidsinterval:
(0,62-0,46) +/- 2,58*√(0,62(1-0,62)/100 + 0,46(1-0,46)/100) = [-0,0192, 0,3392]
Opmerking: u kunt deze betrouwbaarheidsintervallen ook vinden met behulp van de calculator voor het betrouwbaarheidsinterval voor het verschil in verhoudingen .
CI voor het verschil in verhoudingen : interpretatie
De manier waarop we een betrouwbaarheidsinterval zouden interpreteren is:
Er is een kans van 95% dat het betrouwbaarheidsinterval van [.0236, .2964] het werkelijke verschil bevat in het aandeel inwoners dat de wet tussen de twee provincies steunt.
Aangezien dit interval niet de waarde „0“ bevat, betekent dit dat het zeer waarschijnlijk is dat er een reëel verschil is in het aandeel inwoners dat deze wet steunt in County A vergeleken met County B.