Hoe u een betrouwbaarheidsinterval voor een oddsratio kunt berekenen

Bij het analyseren van een 2×2-tabel berekenen we vaak een oddsratio , die het volgende formaat heeft:

De odds ratio vertelt ons de verhouding tussen de waarschijnlijkheid dat een gebeurtenis optreedt in een behandelgroep en de waarschijnlijkheid dat een gebeurtenis optreedt in een controlegroep. Het wordt als volgt berekend:

• Odds-ratio = (A*D) / (B*C)

We kunnen dan de volgende formule gebruiken om een betrouwbaarheidsinterval voor de odds ratio te berekenen:

• BI minder dan 95% = e ^{ln(OR) – 1,96√ (1/a + 1/b + 1/c + 1/d)}
• BI groter dan 95% = e ^{ln(OR) + 1,96√ (1/a + 1/b + 1/c + 1/d)}

Het volgende voorbeeld laat zien hoe u in de praktijk een oddsratio en een bijbehorend betrouwbaarheidsinterval kunt berekenen.

Voorbeeld: Berekening van een betrouwbaarheidsinterval voor een oddsratio

Stel dat een basketbalcoach een nieuw trainingsprogramma gebruikt om te kijken of dit het aantal spelers dat een bepaalde vaardigheidstest kan halen vergroot, vergeleken met een oud trainingsprogramma.

De coach rekruteert 50 spelers om elk programma te gebruiken. De volgende tabel toont het aantal spelers dat wel of niet slaagde voor de vaardigheidstest, gebaseerd op het programma dat ze gebruikten:

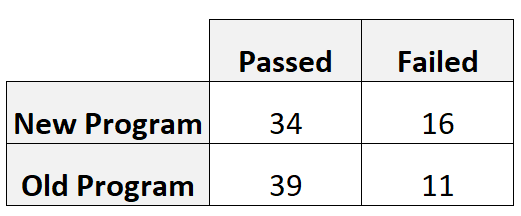
We kunnen de oddsratio berekenen als (34*11) / (16*39) = 0,599

We zouden dit zo interpreteren dat de kans dat een speler slaagt voor de test met het nieuwe programma slechts 0,599 keer zo groot is als de kans dat een speler de test haalt met het oude programma.

Met andere woorden: de kans dat een speler de test doorstaat, wordt dankzij het nieuwe programma zelfs met 40,1% verkleind.

We kunnen dan de volgende formules gebruiken om het 95% betrouwbaarheidsinterval voor de odds ratio te berekenen:

• BI minder dan 95% = e ^{ln (0,599) – 1,96√ (1/34 + 1/16 + 1/39 + 1/11)} = 0,245
• Groter dan 95% BI = e ^{ln (0,599) + 1,96√ (1/34 + 1/16 + 1/39 + 1/11)} = 1,467

Het 95% betrouwbaarheidsinterval voor de odds ratio is dus [0,245; 1,467] .

We zijn er 95% zeker van dat de werkelijke odds ratio tussen het nieuwe en het oude trainingsprogramma binnen dit interval ligt.

Omdat dit betrouwbaarheidsinterval de waarde 1 bevat, is het niet statistisch significant.

Dit zou logisch moeten zijn als je het volgende in overweging neemt:

• Een odds ratio groter dan 1 zou betekenen dat de kans dat een speler de test met het nieuwe programma haalt groter is dan de kans dat een speler de test met het oude programma haalt.
• Een odds ratio kleiner dan 1 zou betekenen dat de kans dat een speler de test met het nieuwe programma haalt kleiner is dan de kans dat een speler de test met het oude programma haalt.

Omdat ons 95% betrouwbaarheidsinterval voor de oddsratio de waarde 1 bevat, betekent dit dat de kans dat een speler de vaardigheidstest met het nieuwe programma haalt wel of niet groter kan zijn dan de kans dat dezelfde speler de test haalt. met behulp van het nieuwe programma. oud programma.

Aanvullende bronnen

De volgende tutorials bieden meer informatie over het interpreteren van oddsratio’s:

Hoe oddsratio’s te interpreteren
Wat is een aangepaste oddsratio?
Hoe interpreteer je een odds ratio kleiner dan 1?
Hoe u de oddsratio en het relatieve risico in Excel kunt berekenen