Betrouwbaarheidsinterval voor het verschil in gemiddelden
In dit artikel wordt uitgelegd wat een betrouwbaarheidsinterval voor het verschil in gemiddelden in de statistiek is en waarvoor het wordt gebruikt. U zult dus ontdekken hoe u het betrouwbaarheidsinterval voor het verschil van twee gemiddelden kunt berekenen en een oefening die u stap voor stap kunt oplossen.
Wat is het betrouwbaarheidsinterval voor het verschil in gemiddelden?
Het betrouwbaarheidsinterval voor het verschil in gemiddelden is een interval dat een maximumwaarde en een minimumwaarde oplevert waartussen de waarde van het verschil in gemiddelden van twee populaties met een bepaald betrouwbaarheidsniveau ligt.
Als het betrouwbaarheidsinterval voor het verschil in de gemiddelden van twee populaties met een betrouwbaarheidsniveau van 95% bijvoorbeeld (3,5) is, betekent dit dat het verschil tussen de gemiddelden van de twee populaties tussen 3 en 5 zal liggen met een waarschijnlijkheid van 95. %.
Daarom wordt in de statistieken het betrouwbaarheidsinterval voor het verschil in gemiddelden gebruikt om twee waarden te schatten waartussen het verschil tussen twee populatiegemiddelden ligt. Met behulp van gegevens uit twee steekproeven is het dus mogelijk om het verschil tussen de populatiegemiddelden te benaderen.
Betrouwbaarheidsintervalformule voor verschil in gemiddelden
De formule voor het betrouwbaarheidsinterval voor het verschil in gemiddelden hangt af van het feit of de populatievarianties al dan niet bekend zijn en, zo niet, of kan worden aangenomen dat de populatievarianties gelijk zijn. . Vervolgens zullen we zien hoe het betrouwbaarheidsinterval voor het verschil in gemiddelden telkens wordt berekend.
bekende afwijkingen
De formule voor het berekenen van het betrouwbaarheidsinterval voor het verschil in gemiddelden wanneer de varianties van de twee populaties bekend zijn met een betrouwbaarheidsniveau van 1-α is als volgt:
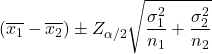
Goud:
-

is het gemiddelde van monster i.
-

is de standaarddeviatie van populatie i.
-

is de waarde van de standaardnormale verdeling met waarschijnlijkheid α/2.
-

is de steekproefomvang i.
Dit geval komt het minst vaak voor, omdat de waarde van populatievarianties over het algemeen onbekend is.
onbekende en gelijke varianties
Wanneer de varianties van de twee populaties onbekend zijn, maar geschat kunnen worden als gelijk, is de formule voor het berekenen van het betrouwbaarheidsinterval voor het verschil tussen gemiddelden met een betrouwbaarheidsniveau van 1-α als volgt:
![]()
Goud:
-

is het gemiddelde van monster i.
-

is de gepoolde standaarddeviatie.
-

is de waarde van de Student’s t-verdeling van n 1 + n 2 -2 vrijheidsgraden met een waarschijnlijkheid van α/2.
-

is de steekproefomvang i.
Omdat in dit geval wordt aangenomen dat de populatievarianties equivalent zijn, wordt de gecombineerde standaarddeviatie gebruikt om het betrouwbaarheidsinterval te berekenen, dat wordt berekend met de volgende formule:

Goud
![]()
is de standaardafwijking van monster i.
Onbekende en verschillende varianten
Wanneer de varianties van de twee populaties onbekend zijn en er niet van kan worden uitgegaan dat ze gelijk zijn, is de formule voor het berekenen van het betrouwbaarheidsinterval voor het verschil tussen gemiddelden met een betrouwbaarheidsniveau van 1-α als volgt:
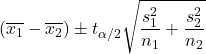
Goud:
-

is het gemiddelde van monster i.
-
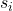
is de standaardafwijking van monster i.
-

is de waarde van de Student’s t-verdeling met een waarschijnlijkheid van α/2.
-

is de steekproefomvang i.
In dit geval worden de vrijheidsgraden van de Student’s t-verdeling berekend met behulp van de volgende formule:

Goud
![]()
is de standaardafwijking van monster i.
Concreet voorbeeld van het betrouwbaarheidsinterval voor het verschil in gemiddelden
Nadat we de definitie van het betrouwbaarheidsinterval voor het verschil tussen gemiddelden hebben gezien en wat de verschillende formules zijn, zullen we nu een concreet voorbeeld zien om te voltooien hoe het betrouwbaarheidsinterval voor het verschil tussen twee gemiddelden wordt berekend.
- Wij willen het effect van tabak op het geboortegewicht van kinderen onderzoeken. Om dit te doen worden twee steekproeven vergeleken: de eerste steekproef bestaat uit kinderen van wie de moeders niet rookten en de tweede steekproef bestaat uit kinderen van wie de moeders rookten (de steekproefparameters worden hieronder aangegeven). Bereken het betrouwbaarheidsinterval voor het verschil in gemiddelden met een betrouwbaarheidsniveau van 95%.
- Niet-rokende moeders:
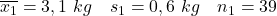
- Rokende moeders:
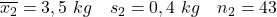
- Niet-rokende moeders:
In dit geval kennen we de waarden van de populatievarianties niet, maar we kunnen ervan uitgaan dat de populatievarianties gelijkwaardig zijn, omdat we te maken hebben met twee populaties met zeer vergelijkbare kenmerken. Daarom is de formule voor het betrouwbaarheidsinterval voor het verschil in middelen die we moeten gebruiken:
![]()
We berekenen dus de gecombineerde standaardafwijking van de standaardafwijkingen van de twee steekproeven:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
Op dezelfde manier moeten we de waarde van de Student’s t-verdeling van 80 vrijheidsgraden met een waarschijnlijkheid van 2,5% vinden in de waarschijnlijkheidsverdelingstabel van de Student’s t-verdeling :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
Ten slotte vervangen we de gegevens in de betrouwbaarheidsintervalformule voor het verschil in gemiddelden en voeren we de berekeningen uit:
![]()
![]()
![]()
Het betrouwbaarheidsinterval voor het verschil in gemiddelden van het probleem is daarom als volgt:
![]()