Betrouwbaarheidsinterval voor proportie

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat het betrouwbaarheidsinterval voor proporties is en waarvoor het in de statistieken wordt gebruikt. Op dezelfde manier ontdekt u hoe u het betrouwbaarheidsinterval van de verhouding kunt berekenen, evenals een opgeloste oefening om het concept beter te begrijpen.

Wat is het betrouwbaarheidsinterval van de proportie?

Het betrouwbaarheidsinterval voor proporties is een interval dat een reeks toelaatbare waarden biedt voor het proportie van een populatie. Dat wil zeggen dat het betrouwbaarheidsinterval voor de proportie een maximumwaarde en een minimumwaarde aangeeft waartussen de populatieproportie met een foutmarge ligt.

Als het betrouwbaarheidsinterval voor het aandeel van een populatie met een betrouwbaarheidsniveau van 95% bijvoorbeeld (0,73; 0,81) is, betekent dit dat het aandeel van een populatie tussen 73% en 81% ligt met een waarschijnlijkheid van 95%.

Daarom wordt het betrouwbaarheidsinterval van het aandeel gebruikt om de waarde te schatten van het aandeel van een populatie dat aan bepaalde kenmerken voldoet.

Zoals we in de volgende paragraaf zullen zien, hangt het betrouwbaarheidsinterval voor de proportie af van de steekproefproportie en het aantal waarnemingen in de steekproef.

Betrouwbaarheidsintervalformule voor proporties

Het betrouwbaarheidsinterval voor het aandeel wordt berekend door het optellen en aftrekken van het steekproefaandeel van de waarde van Z _α/2 vermenigvuldigd met de vierkantswortel van het steekproefaandeel (p), vermenigvuldigd met 1-p en gedeeld door de steekproefomvang (n). Daarom is de formule voor het berekenen van het betrouwbaarheidsinterval voor het aandeel :

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

Goud:

$p$

is de steekproefaandeel.
$n$

is de steekproefomvang.
$Z_{\alpha/2}$

is het kwantiel van de standaardnormale verdeling dat overeenkomt met een waarschijnlijkheid van α/2. Voor grote steekproeven en een betrouwbaarheidsniveau van 95% ligt dit gewoonlijk dicht bij 1,96 en voor een betrouwbaarheidsniveau van 99% ligt het gewoonlijk dicht bij 2,576.

Voorbeeld van het berekenen van een betrouwbaarheidsinterval voor proporties

Om u te laten zien hoe een betrouwbaarheidsinterval voor het aandeel wordt berekend, laten we hieronder stap voor stap een concreet voorbeeld achter.

Een verzekeringsmaatschappij wil marktonderzoek doen en bepalen hoeveel mensen in een land een levensverzekering hebben. Om dit te doen wordt een willekeurige steekproef van 700 mensen geanalyseerd en komen we tot de conclusie dat 40% van de steekproef een levensverzekering heeft. Wat is het betrouwbaarheidsinterval bij een betrouwbaarheidsniveau van 95% voor het aandeel van de bevolking van het land?

Om het betrouwbaarheidsinterval van het populatieaandeel te bepalen, moeten we de formule gebruiken die we hierboven hebben gezien:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

In dit geval willen we dat het betrouwbaarheidsniveau van het betrouwbaarheidsinterval 95% is, dus de waarde van Z _α/2 die we moeten nemen is 1,96.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

De probleemstelling vertelt ons al dat de steekproefomvang n=700 is en het waargenomen aandeel in de steekproef p=0,40 is, dus vervangen we de gegevens in de betrouwbaarheidsintervalformule voor het aandeel en berekenen we de grenzen van het interval:

$\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)$

$\displaystyle \left(0,40-1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}}\ , \ 0,40+1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}\right)$

$\displaystyle \left(0,36 \ , \ 0,44\right)$

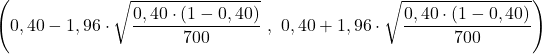
Concluderend kan worden gesteld dat het aandeel van de onderzochte populatie tussen 36% en 44% ligt, met een betrouwbaarheidsniveau van 95%.

➤ Zie: Betrouwbaarheidsinterval voor het gemiddelde
➤ Zie: Betrouwbaarheidsinterval voor variantie

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder

Wat is het betrouwbaarheidsinterval van de proportie?

Betrouwbaarheidsintervalformule voor proporties

Voorbeeld van het berekenen van een betrouwbaarheidsinterval voor proporties

Über den Autor

Dr.benjamin anderson

Einen Kommentar hinzufügen