Excel: bereken het betrouwbaarheidsinterval voor de regressiecoëfficiënt

In een lineair regressiemodel vertelt een regressiecoëfficiënt ons de gemiddelde verandering in deresponsvariabele die gepaard gaat met een toename van één eenheid in de voorspellende variabele.

We kunnen de volgende formule gebruiken om een betrouwbaarheidsinterval voor een regressiecoëfficiënt te berekenen:

Betrouwbaarheidsinterval voor β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

Goud:

•   b ₁ = Regressiecoëfficiënt weergegeven in de regressietabel
• t _{1-∝/2, n-2} = De kritische t-waarde voor het 1-∝ betrouwbaarheidsniveau met n-2 vrijheidsgraden waarbij n het totale aantal waarnemingen in onze dataset is
• se(b ₁ ) = De standaardfout van b ₁ weergegeven in de regressietabel

Het volgende voorbeeld laat zien hoe u een betrouwbaarheidsinterval voor een regressiecoëfficiënt in Excel kunt berekenen.

Voorbeeld: betrouwbaarheidsinterval voor regressiecoëfficiënt in Excel

Stel dat we een eenvoudig lineair regressiemodel willen toepassen met bestudeerde uren als voorspellende variabele en examenscores als responsvariabele voor 15 leerlingen in een bepaalde klas:

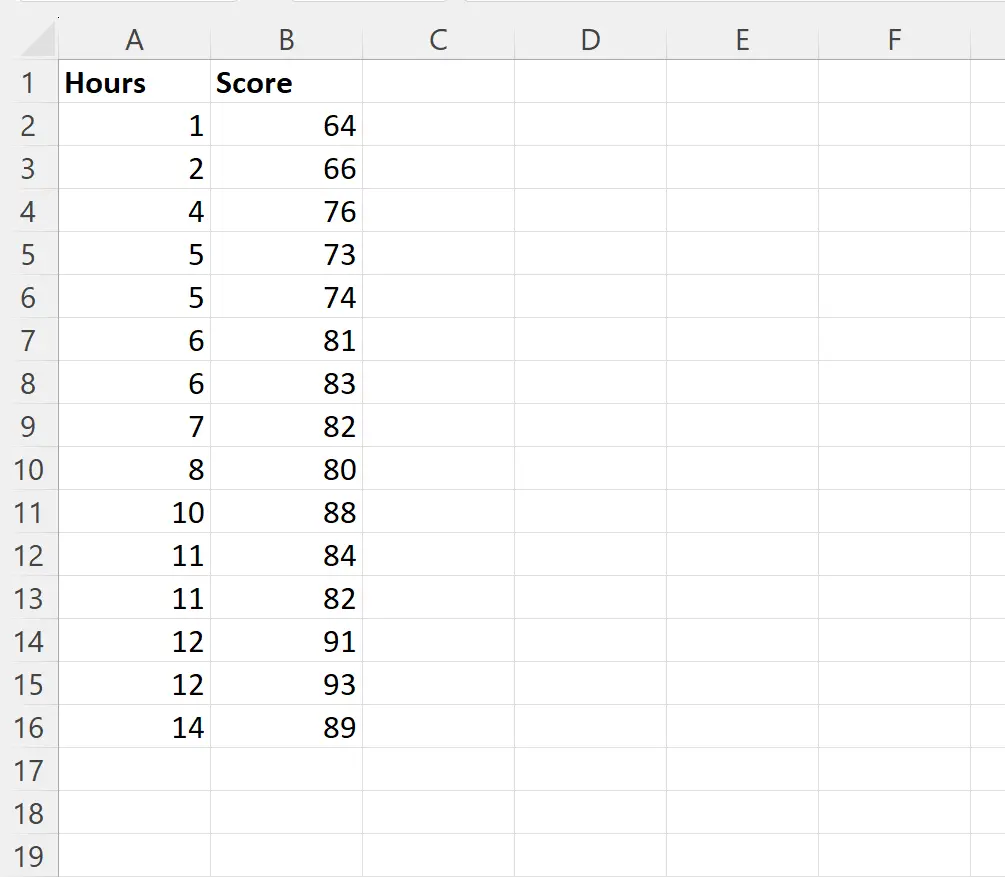
We kunnen de volgende formule in cel D2 typen om een eenvoudige lineaire regressie uit te voeren met de waarden in de kolom Uren als voorspellende variabele en de waarden in de kolom Score als responsvariabele:

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

Merk op dat het eerste WAAR- argument Excel vertelt om het snijpunt van de regressievergelijking normaal te berekenen zonder te forceren dat deze nul is.

Het tweede TRUE- argument vertelt Excel om naast de coëfficiënten aanvullende regressiestatistieken te produceren.

De volgende schermafbeelding toont het resultaat van deze formule (we leggen uit wat elke uitvoerwaarde vertegenwoordigt in de rode tekst onder de uitvoer):

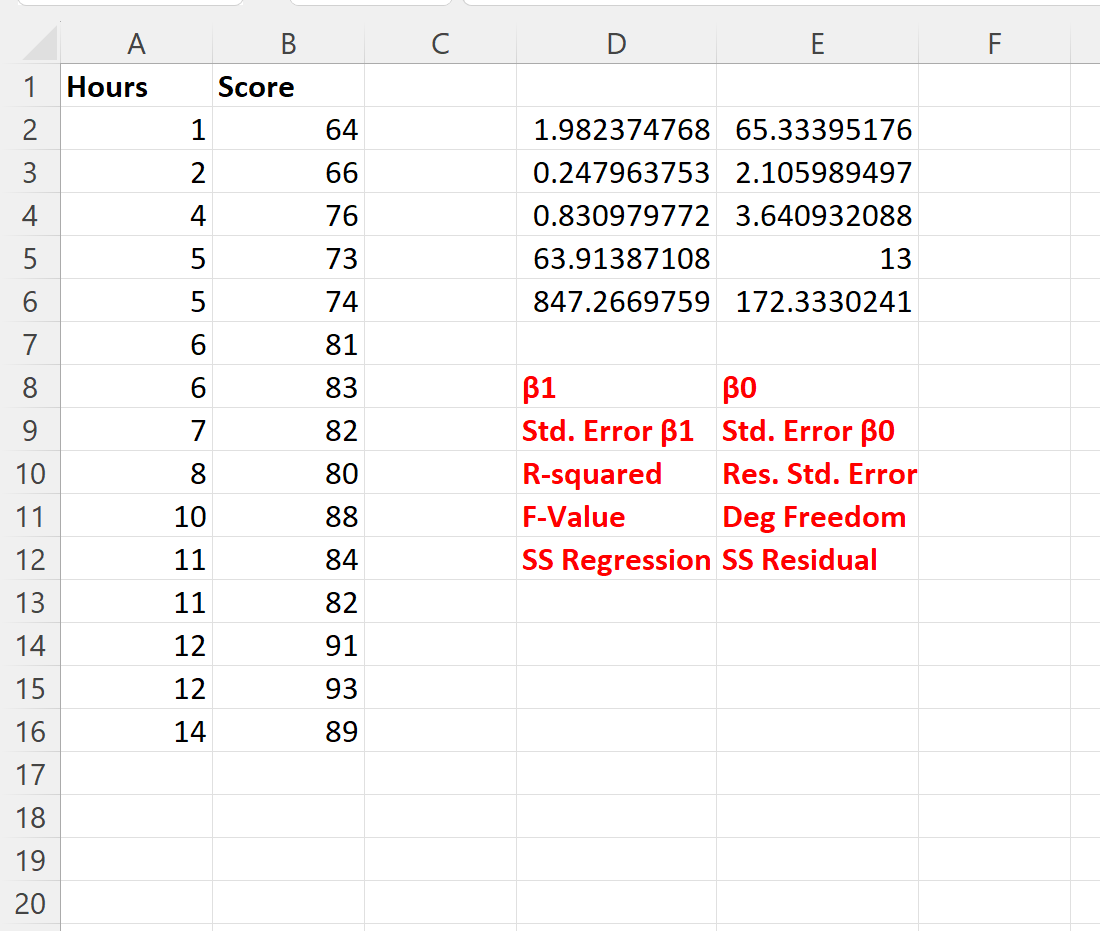
Met behulp van de regressiecoëfficiënten kunnen we de aangepaste regressievergelijking als volgt schrijven:

Score = 65.334 + 1.982*(Uren bestudeerd)

Merk op dat de regressiecoëfficiënt voor uren 1,982 is.

Dit vertelt ons dat elk extra uur studietijd gepaard gaat met een gemiddelde stijging van 1.982 in de examenscore.

Om een betrouwbaarheidsinterval van 95% voor de regressiecoëfficiënt te berekenen, kunnen we de volgende formules invoeren in de cellen H2 en H3:

• H2: = D2 – T.INV.2T(0,05, E5)*D3
• H3: = D2 + T.INV.2T(0,05, E5)*D3

De volgende schermafbeelding laat zien hoe u deze formules in de praktijk kunt gebruiken:

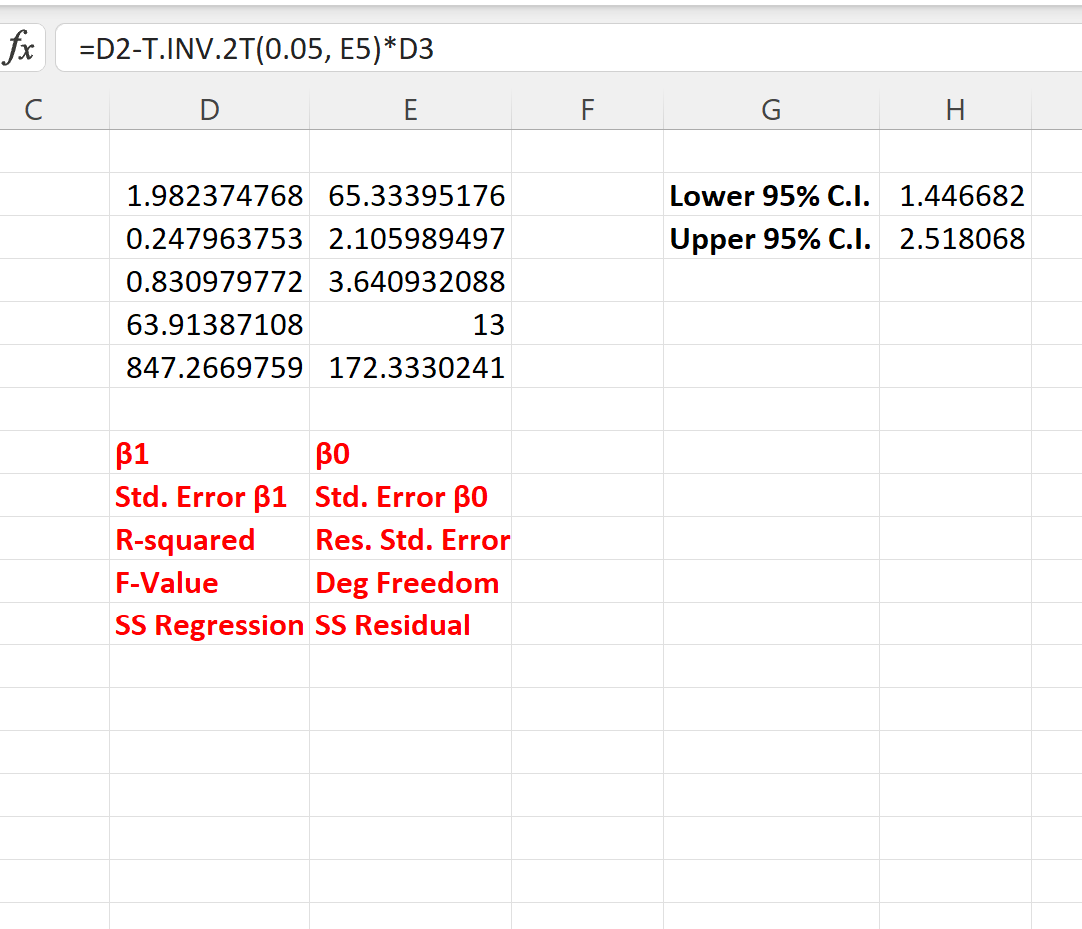
Het 95% betrouwbaarheidsinterval voor de regressiecoëfficiënt is [1,446, 2,518] .

Omdat dit betrouwbaarheidsinterval niet de waarde 0 bevat , kunnen we concluderen dat er een statistisch significant verband bestaat tussen het aantal gestudeerde uren en het examencijfer.

We kunnen ook bevestigen dat dit correct is door handmatig het 95% betrouwbaarheidsinterval voor de regressiecoëfficiënt te berekenen:

• 95% BI voor β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )
• 95% BI voor β ₁ : 1,982 ± t _{0,975, 15-2} * 0,248
• 95% BI voor β ₁ : 1,982 ± 2,1604 * 0,248
• 95% BI voor β ₁ : [1,446, 2,518]

Het 95% betrouwbaarheidsinterval voor de regressiecoëfficiënt is [1,446, 2,518] .

Aanvullende bronnen

In de volgende zelfstudies wordt uitgelegd hoe u andere veelvoorkomende taken in Excel kunt uitvoeren:

Hoe u eenvoudige lineaire regressie uitvoert in Excel
Hoe u meerdere lineaire regressies uitvoert in Excel
Hoe P-waarden te interpreteren in regressie-uitvoer in Excel