Bevolking betekent

Von Dr.benjamin anderson August 3, 2023 Statistieken Keine Kommentare

In dit artikel wordt uitgelegd wat populatie in de statistieken betekent. Op dezelfde manier zul je ontdekken wat de formule is voor het populatiegemiddelde, hoe het betrouwbaarheidsinterval van het populatiegemiddelde wordt berekend en bovendien wat het verschil is tussen het populatiegemiddelde en het gemiddelde van de steekproef.

Wat is het bevolkingsgemiddelde?

Het populatiegemiddelde is het rekenkundig gemiddelde van alle elementen van de statistische populatie. Om het populatiegemiddelde te berekenen, moeten daarom alle populatiewaarden worden opgeteld en vervolgens worden gedeeld door het totale aantal elementen in de populatie.

Het symbool voor het populatiegemiddelde is de Griekse letter μ.

Op dezelfde manier kan het populatiegemiddelde ook worden gedefinieerd als de verwachte waarde van de variabele die een populatie vertegenwoordigt.

Hoe het bevolkingsgemiddelde te berekenen

Als we eenmaal de definitie van het populatiegemiddelde hebben gezien, gaan we kijken hoe het populatiegemiddelde wordt berekend om de betekenis ervan beter te begrijpen.

Als alle waarden in de statistische populatie bekend zijn, moet de formule voor het rekenkundig gemiddelde eenvoudigweg worden toegepast om het populatiegemiddelde te berekenen. Om het populatiegemiddelde te berekenen, moeten we in dit geval dus alle populatiewaarden bij elkaar optellen en vervolgens delen door het totale aantal gegevens.

Als we dus de waarde van alle elementen van de populatie kennen, is de formule om het populatiegemiddelde te berekenen als volgt:

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ Zie: Voorbeeld van berekening van het rekenkundig gemiddelde

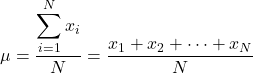
Over het algemeen zijn echter niet alle populatiewaarden bekend, dus normaal gesproken wordt de waarde van het populatiegemiddelde geschat met intervallen .

Betrouwbaarheidsinterval voor populatiegemiddelde

In de praktijk is het onmogelijk om alle individuen in een populatie te bestuderen, dus wordt normaal gesproken een willekeurige steekproef van de populatie gekozen en op basis van de waarden ervan wordt een benadering van de waarde van het populatiegemiddelde gemaakt. Preciezer gezegd: we berekenen een interval waarin het gemiddelde van de gehele populatie zeer waarschijnlijk zal liggen; dit interval wordt het betrouwbaarheidsinterval voor het populatiegemiddelde genoemd.

Het betrouwbaarheidsinterval voor het populatiegemiddelde wordt berekend door het optellen en aftrekken van het steekproefgemiddelde van de waarde van Z _α/2 vermenigvuldigd met de standaarddeviatie (σ) en gedeeld door de vierkantswortel van de hoogte van het monster (n). Daarom is de formule voor het berekenen van het betrouwbaarheidsinterval voor het populatiegemiddelde:

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

De bovenstaande formule wordt gebruikt als de populatievariantie bekend is. Als de populatievariantie echter onbekend is, wat het meest voorkomende geval is, wordt het betrouwbaarheidsinterval voor het gemiddelde berekend met behulp van de volgende formule:

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

Goud:

$\overline{x}$

is het steekproefgemiddelde.
$t_{\alpha/2}$

is de waarde van de Student’s t-verdeling van n-1 vrijheidsgraden met waarschijnlijkheid α/2. Voor grote steekproeven en een betrouwbaarheidsniveau van 95% ligt dit gewoonlijk dicht bij 1,96 en voor een betrouwbaarheidsniveau van 99% ligt het gewoonlijk dicht bij 2,576.
$s$

is de standaardafwijking van het monster.
$n$

is de steekproefomvang.

➤ Zie: Voorbeeld van het berekenen van het betrouwbaarheidsinterval voor het populatiegemiddelde

Populatiegemiddelde en steekproefgemiddelde

Ten slotte zullen we, samengevat, de verschillen tussen het populatiegemiddelde en het steekproefgemiddelde bekijken, zodat deze twee statistische concepten duidelijk zijn.

Het verschil tussen het populatiegemiddelde en het steekproefgemiddelde is het bereik van waarden waarover het gemiddelde wordt berekend. Het populatiegemiddelde is het gemiddelde van de gehele statistische populatie, terwijl het steekproefgemiddelde het gemiddelde is van een steekproef van de populatie.

Om het populatiegemiddelde te onderscheiden van het steekproefgemiddelde, worden ze bovendien weergegeven door verschillende symbolen. Het symbool voor het populatiegemiddelde is

$\mu$

Aan de andere kant is het symbool voor de steekproefgemiddelden

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

Als u nog twijfelt over de verschillen tussen deze twee soorten gemiddelden of meer wilt weten over het berekenen van het steekproefgemiddelde, kunt u het volgende artikel raadplegen:

➤ Zie: Wat betekent het monster?

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder