Wat is de afweging tussen bias en variantie bij machinaal leren?

Om de prestaties van een model op een dataset te evalueren, moeten we meten hoe goed de voorspellingen van het model overeenkomen met de waargenomen gegevens.

Voor regressiemodellen is de meest gebruikte metriek de gemiddelde kwadratische fout (MSE), die als volgt wordt berekend:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

Goud:

• n: totaal aantal waarnemingen
• y _i : De responswaarde van de ^i-de waarneming
• f( _xi ): De voorspelde responswaarde van de i- ^de waarneming

Hoe dichter de modelvoorspellingen bij de waarnemingen liggen, hoe lager de MSE zal zijn.

Het gaat ons echter alleen om de MSE-test – de MSE – als ons model wordt toegepast op onzichtbare gegevens. Dit komt omdat het ons alleen uitmaakt hoe het model zal presteren op onbekende gegevens, en niet op bestaande gegevens.

Het is bijvoorbeeld prima als een model dat aandelenkoersen voorspelt een lage MSE heeft op basis van historische gegevens, maar we willen het model echt kunnen gebruiken om toekomstige gegevens nauwkeurig te voorspellen.

Het blijkt dat de MSE-test nog steeds in twee delen kan worden opgesplitst:

(1) Variantie: verwijst naar de mate waarin onze functie f zou veranderen als we deze schatten met behulp van een andere trainingsset.

(2) Bias: verwijst naar de fout die wordt geïntroduceerd door een reëel probleem, dat extreem ingewikkeld kan zijn, te benaderen met een veel eenvoudiger model.

In wiskundige termen geschreven:

MSE-test = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE-test = Variantie + Bias ² + Onherleidbare fout

De derde term, de onherleidbare fout, is de fout die door geen enkel model kan worden verminderd, simpelweg omdat er altijd ruis zit in de relatie tussen de reeks verklarende variabelen en de responsvariabele .

Modellen met een hoge bias hebben doorgaans een lage variantie . Lineaire regressiemodellen hebben bijvoorbeeld de neiging een hoge bias te hebben (uitgaande van een eenvoudig lineair verband tussen de verklarende variabelen en de responsvariabele) en een lage variantie (de modelschattingen zullen van steekproef tot steekproef niet veel veranderen). de andere).

Modellen met een lage bias hebben echter doorgaans een hoge variantie . Complexe niet-lineaire modellen hebben bijvoorbeeld de neiging een lage bias te hebben (ga niet uit van een bepaalde relatie tussen de verklarende variabelen en de responsvariabele) met een hoge variantie (modelschattingen kunnen aanzienlijk veranderen van de ene leersteekproef naar de andere).

De afweging tussen bias en variantie

De afruil tussen bias en variantie verwijst naar de afweging die plaatsvindt wanneer we ervoor kiezen om bias te verminderen, wat doorgaans de variantie vergroot, of om variantie te verminderen, wat doorgaans de bias vergroot.

De volgende grafiek biedt een manier om deze afweging te visualiseren:

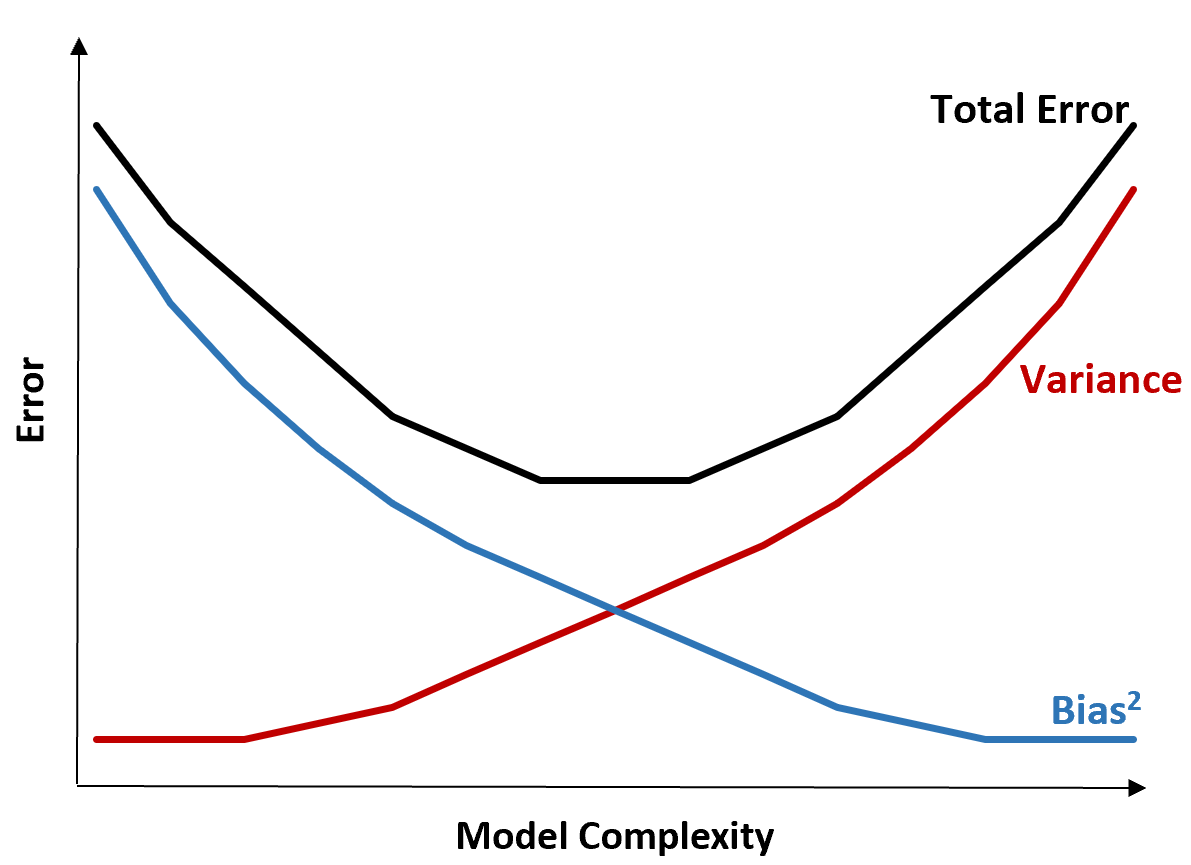
De totale fout neemt af naarmate de complexiteit van een model toeneemt, maar slechts tot op zekere hoogte. Voorbij een bepaald punt begint de variantie toe te nemen en begint ook de totale fout toe te nemen.

In de praktijk gaat het ons alleen om het minimaliseren van de totale fout van een model, en niet noodzakelijkerwijs om het minimaliseren van de variantie of vertekening. Het blijkt dat de manier om de totale fout te minimaliseren het vinden van de juiste balans tussen variantie en vertekening is.

Met andere woorden: we willen een model dat complex genoeg is om de ware relatie tussen de verklarende variabelen en de responsvariabele vast te leggen, maar niet te complex om patronen te detecteren die in werkelijkheid niet bestaan.

Wanneer een model te complex is, past het de gegevens te veel aan. Dit gebeurt omdat het te moeilijk is om patronen in de trainingsgegevens te vinden die eenvoudigweg door toeval worden veroorzaakt. Dit type model presteert waarschijnlijk slecht op onzichtbare gegevens.

Maar als een model te simpel is, onderschat het de gegevens. Dit gebeurt omdat wordt aangenomen dat de werkelijke relatie tussen de verklarende variabelen en de responsvariabele eenvoudiger is dan deze in werkelijkheid is.

De manier om optimale modellen in machinaal leren te selecteren is door een balans te vinden tussen vertekening en variantie om de fout bij het testen van het model op toekomstige onzichtbare gegevens te minimaliseren.

In de praktijk is de meest gebruikelijke manier om de MSE van tests te minimaliseren het gebruik van kruisvalidatie .