Handmatig een tweerichtings-anova uitvoeren

Een tweerichtings-ANOVA wordt gebruikt om te bepalen of er al dan niet een statistisch significant verschil bestaat tussen de gemiddelden van drie of meer onafhankelijke groepen die over twee factoren zijn verdeeld.

In deze zelfstudie wordt uitgelegd hoe u handmatig een tweerichtings-ANOVA uitvoert.

Voorbeeld: Handmatige tweeweg-ANOVA

Stel dat een botanicus wil weten of de plantengroei wordt beïnvloed door blootstelling aan zonlicht en de frequentie van water geven. Ze plant 40 zaden en laat ze een maand lang groeien onder verschillende omstandigheden van blootstelling aan de zon en waterfrequentie.

Na een maand registreert ze de hoogte van elke plant. De resultaten worden hieronder weergegeven:

In de bovenstaande tabel zien we dat er onder elke combinatie van omstandigheden vijf planten werden gekweekt.

Er werden bijvoorbeeld vijf planten gekweekt met dagelijks water en zonder zonlicht en hun hoogten na twee maanden waren 4,8 inch, 4,4 inch, 3,2 inch, 3,9 inch en 4,4 inch:

We kunnen de volgende stappen gebruiken om een tweerichtings-ANOVA uit te voeren:

Stap 1: Bereken de som van de kwadraten voor de eerste factor (bewateringsfrequentie)

Eerst berekenen we de totale gemiddelde hoogte van de 40 planten:

Algemeen gemiddelde = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Vervolgens berekenen we de gemiddelde hoogte van alle planten die dagelijks water krijgen:

Daggemiddelde = (4,8 + 5 + 6,4 + 6,3 + … + 4,4 + 4,8 + 5,8 + 5,8) /20 = 5,155

Vervolgens berekenen we de gemiddelde hoogte van alle planten die elke week water krijgen:

Weekgemiddelde = (4,4 + 4,9 + 5,8 + 6 + … + 3,9 + 4,8 + 5,5 + 5,5) /20 = 5,15

Vervolgens berekenen we de som van de kwadraten voor de factor “besproeiingsfrequentie” met behulp van de volgende formule:

Σn( _Xj – X ..) ²

Goud:

• n : de steekproefomvang van groep j
• Σ : een Grieks symbool dat “som” betekent
• _Xj : het gemiddelde van groep j
• X .. : het mooie gemiddelde

In ons voorbeeld berekenen we de som van de kwadraten voor de factor “besproeiingsfrequentie” als volgt: 20(5,155-5,1525) ² + 20(5,15-5,1525) ² = 0,00025

Stap 2: Bereken de som van de kwadraten voor de tweede factor (blootstelling aan de zon)

Eerst berekenen we de totale gemiddelde hoogte van de 40 planten:

Algemeen gemiddelde = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Vervolgens berekenen we de gemiddelde hoogte van alle planten die niet aan de zon zijn blootgesteld:

Gemiddeld zonder zon = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07

We zullen deze berekening herhalen om de gemiddelde hoogte te vinden van planten die zijn blootgesteld aan verschillende blootstelling aan de zon:

• Laag zonneschijngemiddelde = 5,1
• Gemiddeld gemiddeld zonlicht = 5,89
• Gemiddelde hoge zonneschijn = 5,55

Vervolgens berekenen we de som van de kwadraten voor de factor ‘blootstelling aan de zon’ met behulp van de volgende formule:

Σn( _Xj – X ..) ²

Goud:

• n : de steekproefomvang van groep j
• Σ : een Grieks symbool dat “som” betekent
• _Xj : het gemiddelde van groep j
• X .. : het mooie gemiddelde

In ons voorbeeld berekenen we de som van de kwadraten voor de factor ‘blootstelling aan de zon’ als volgt: 10(4,07-5,1525) ² + 10(5,1-5,1525) ² + 10(5,89 -5,1525) ² + 10(5,55-5,1525) ² = 18,76475

Stap 3: Bereken de som van de kwadraten binnenin (fout)

Vervolgens berekenen we de som van de kwadraten door de som van de kwadraten te nemen van de verschillen tussen elke combinatie van factoren en de individuele planthoogtes.

De gemiddelde hoogte van alle planten die dagelijks worden bewaterd zonder blootstelling aan zonlicht is bijvoorbeeld 4,14. We kunnen dan de som van de kwadraten van de verschillen voor elk van deze individuele planten als volgt berekenen:

• SS voor dagelijks water geven en zonder zon: (4,8-4,14) ² + (4,4-4,14) ² + (3,2-4,14) ² + (3,9-4,14) ² + (4,4-4,14) ² = 1,512

We kunnen dit proces herhalen voor elke combinatie van factoren:

• SS voor dagelijks water geven en weinig zonlicht: 0,928
• SS voor dagelijkse watergift en gemiddelde zonneschijn: 1.788
• SS voor dagelijks water geven en sterk zonlicht: 1.648
• SS voor wekelijkse watergift zonder zon: 0,34
• SS voor wekelijkse watergift en weinig zonlicht: 0,548
• SS voor wekelijkse watergift en gemiddelde zonneschijn: 0,652
• SS voor wekelijkse watergift en sterk zonlicht: 1.268

We kunnen dan de som van al deze waarden nemen om de som van de vierkanten binnenin te vinden (fout):

Sommen van kwadraten binnen = 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684

Stap 4: Bereken de totale som van de kwadraten

Vervolgens kunnen we de totale som van de kwadraten berekenen door de som te nemen van de verschillen tussen de hoogte van elke plant en het eindgemiddelde:

Totale som van kwadraten = (4,8 – 5,1525) ² + (5 – 5,1525) ² + … + (5,5 – 5,1525) ² = 28,45975

Stap 5: Bereken de som van de kwadrateninteractie

Vervolgens berekenen we de som van de kwadrateninteractie met behulp van de volgende formule:

• Interactie SS = SS Totaal – SS Factor 1 – SS Factor 2 – SS Interieur
• SS-interactie = 28,45975 – 0,00025 – 18,76475 – 8,684
• SS-interactie = 1,01075

Stap 6: Vul de ANOVA-tabel in

Ten slotte vullen we de waarden uit de tweeweg-ANOVA-tabel in:

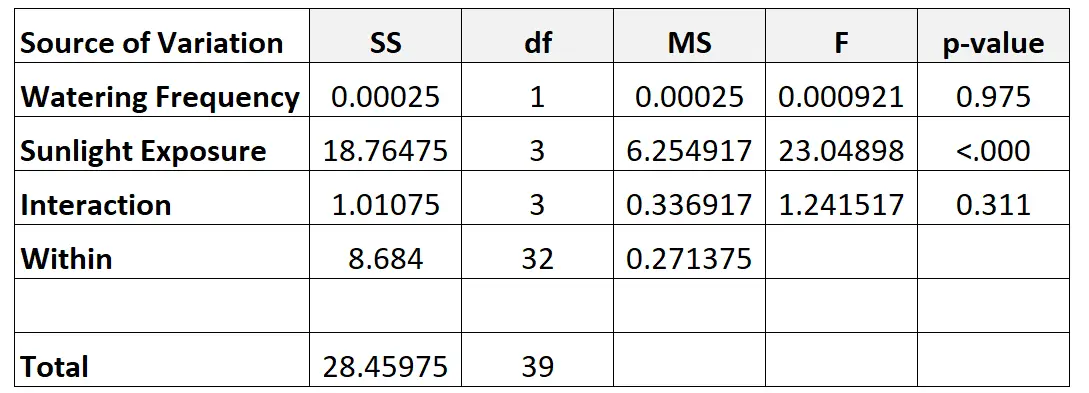
Zo hebben we de verschillende getallen in de tabel berekend:

• df Besproeiingsfrequentie: d-1 = 2-1 = 1
• df Blootstelling aan de zon: k-1 = 4-1 = 3
• dfInteractie : (j-1)*(k-1) = 1*3 = 3
• df In : n – (j*k) = 40 – (2*4) = 32
• totale df: n-1 = 40-1 = 39
• MS: SS/DF
• Besproeiingsfrequentie F : bewateringsfrequentie MS/MS binnenshuis
• F Blootstelling aan zonlicht : MS / MS-blootstelling aan zonlicht binnenshuis
• Interactie F : Interactie MS / MS Binnen
• p-waarde bewateringsfrequentie : De p-waarde die overeenkomt met de F-waarde van 0,000921 met de teller df = 1 en de noemer df = 32
• Blootstelling aan de zon p-waarde : de p-waarde die overeenkomt met de F-waarde van 23,04898 met de teller df = 3 en de noemer df = 32
• p-waarde-interactie : de p-waarde die overeenkomt met de F-waarde van 1,241517 met de teller df = 3 en de noemer df = 32

Opmerking #1: n = totaal aantal waarnemingen, j = aantal niveaus voor bewateringsfrequentie, k = aantal niveaus voor blootstelling aan de zon.

Opmerking #2 : De p-waarden die overeenkomen met de F-waarde zijn berekend met behulp van de F-verdelingscalculator.

Stap 7: Interpreteer de resultaten

Uit de ANOVA-tabel kunnen we het volgende opmaken:

• De p-waarde voor de interactie tussen de waterfrequentie en de blootstelling aan de zon was 0,311 . Dit is niet statistisch significant bij α = 0,05.
• De p-waarde voor de bewateringsfrequentie was 0,975 . Dit is niet statistisch significant bij α = 0,05.
• De p-waarde voor blootstelling aan de zon was <0,000 . Dit is statistisch significant bij α = 0,05.

Deze resultaten geven aan dat blootstelling aan de zon de enige factor is met een statistisch significant effect op de planthoogte.

En aangezien er geen interactie-effect is, is het effect van blootstelling aan de zon consistent op elk niveau van de bewateringsfrequentie.

Simpel gezegd: of een plant dagelijks of wekelijks water krijgt, heeft geen invloed op de invloed van blootstelling aan de zon op een plant.

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over ANOVA’s:

Hoe u handmatig een eenrichtings-ANOVA uitvoert
Handmatig een ANOVA met herhaalde metingen uitvoeren
De complete gids: tweerichtings-ANOVA-resultaten rapporteren