Hoe binomiale kansen te berekenen op een ti-84-rekenmachine

De binominale verdeling is een van de meest gebruikte verdelingen in alle statistieken. In deze tutorial wordt uitgelegd hoe u de volgende functies op een TI-84-rekenmachine kunt gebruiken om binomiale kansen te vinden:

binompdf(n, p, x) retourneert de waarschijnlijkheid die is gekoppeld aan de binominale pdf.

binomcdf(n, p, x) retourneert de cumulatieve waarschijnlijkheid die is gekoppeld aan de binomiale cdf.

Goud:

• n = aantal pogingen
• p = kans op succes bij een bepaalde proef
• x = totaal aantal successen

Deze twee functies zijn toegankelijk op een TI-84-rekenmachine door op 2nd en vervolgens op vars te drukken. Dit brengt je naar een DISTR- scherm waar je vervolgens binompdf() en binomcdf() kunt gebruiken:

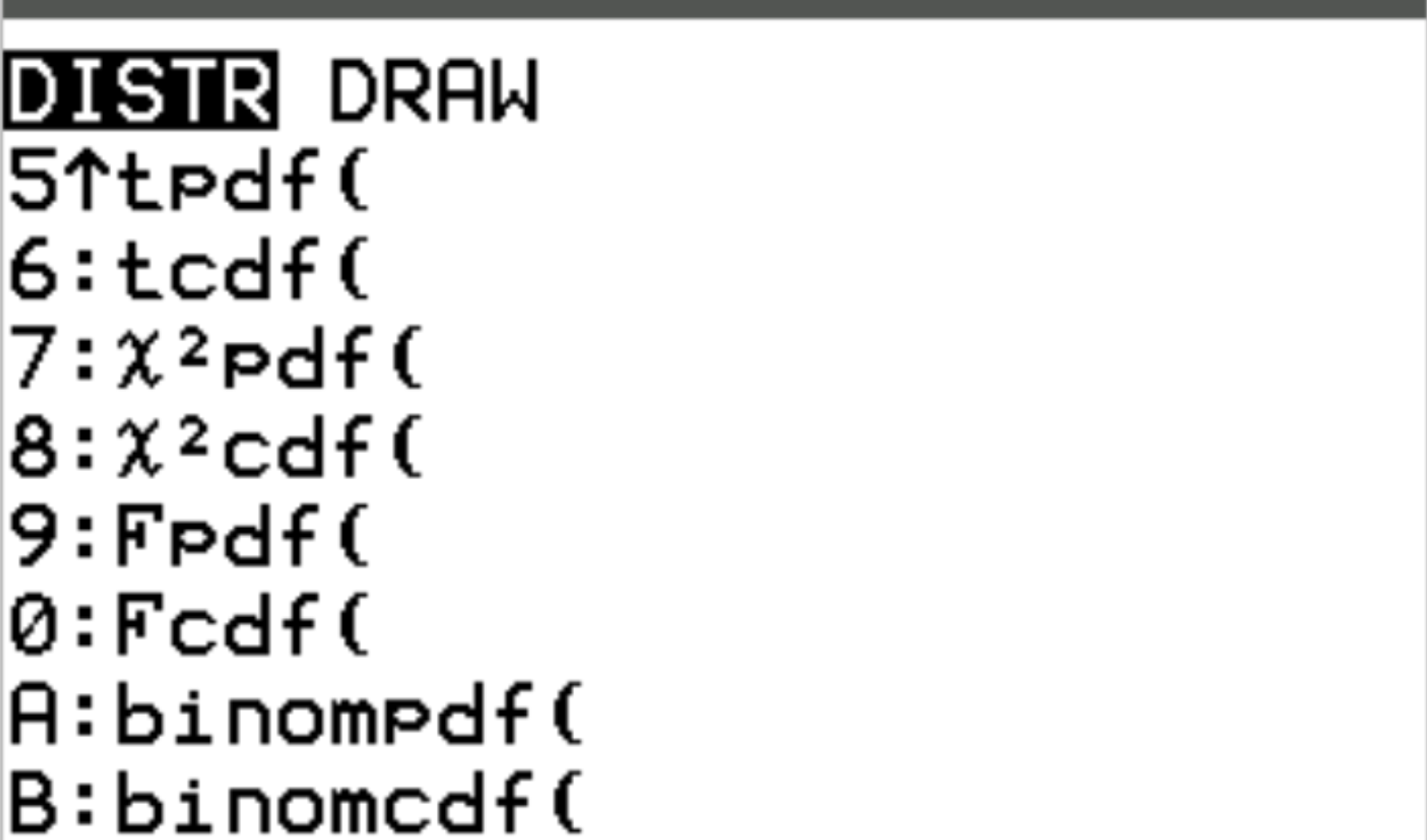
De volgende voorbeelden illustreren hoe u deze functies kunt gebruiken om verschillende vragen te beantwoorden.

Voorbeeld 1: Binomiale waarschijnlijkheid van precies x succes

Vraag: Nathan maakt 60% van zijn vrije worppogingen. Als hij twaalf vrije worpen maakt, wat is dan de kans dat hij er precies tien maakt?

Antwoord: Gebruik de binomialepdf(n, p, x) functie:

binomiaalpdf(12, .60, 10) = 0,0639

Voorbeeld 2: binominale waarschijnlijkheid van minder dan x succes

Vraag: Nathan maakt 60% van zijn vrije worppogingen. Als hij twaalf vrije worpen maakt, wat is dan de kans dat hij er minder dan tien maakt?

Antwoord: Gebruik de binomialcdf(n, p, x-1) functie:

binomiaalcdf(12, .60, 9) = 0,9166

Voorbeeld 3: binominale kans op maximaal x succes

Vraag: Nathan maakt 60% van zijn vrije worppogingen. Als hij twaalf vrije worpen maakt, wat is dan de kans dat hij er maximaal tien maakt?

Antwoord: Gebruik de binomialcdf(n, p, x) functie:

binomiaalcdf(12, .60, 10) = 0,9804

Voorbeeld 4: Binominale waarschijnlijkheid van meer dan x successen

Vraag: Nathan maakt 60% van zijn vrije worppogingen. Als hij twaalf vrije worpen maakt, wat is dan de kans dat hij er meer dan tien maakt?

Antwoord: Gebruik functie 1 – binomialcdf(n, p, x) :

1 – binomiaalcdf(12, .60, 10) = 0,0196

Voorbeeld 5: Binomiale kans op minimaal x succes

Vraag: Nathan maakt 60% van zijn vrije worppogingen. Als hij twaalf vrije worpen maakt, wat is dan de kans dat hij er meer dan tien maakt?

Antwoord: Gebruik functie 1 – binomialcdf(n, p, x-1) :

1 – binomiaalcdf(12, .60, 9) = 0,0834