Hoe binomiale distributie in python te gebruiken
De binominale verdeling is een van de meest gebruikte verdelingen in de statistiek. Het beschrijft de waarschijnlijkheid van het behalen van k successen in n binomiale experimenten.
Als een willekeurige variabele X een binominale verdeling volgt, kan de kans dat X = k succes wordt gevonden met de volgende formule:
P(X=k) = n C k * p k * (1-p) nk
Goud:
- n: aantal pogingen
- k: aantal successen
- p: kans op succes bij een bepaalde proef
- n C k : het aantal manieren om k successen te behalen in n pogingen
In deze tutorial wordt uitgelegd hoe u de binomiale distributie in Python gebruikt.
Hoe een binominale verdeling te genereren
U kunt een array met waarden genereren die een binominale verdeling volgt met behulp van de functie random.binomial van de numpy-bibliotheek:
from numpy import random #generate an array of 10 values that follows a binomial distribution random.binomial(n=10, p=.25, size=10) array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])
Elk getal in de resulterende tabel vertegenwoordigt het aantal „successen“ dat werd ondervonden in de loop van 10 pogingen waarbij de kans op succes in een bepaalde poging 0,25 was.
Hoe kansen te berekenen met behulp van een binominale verdeling
U kunt ook vragen over binomiale waarschijnlijkheid beantwoorden met behulp van de binomfunctie van de scipy-bibliotheek.
Vraag 1: Nathan maakt 60% van zijn vrije worppogingen. Als hij twaalf vrije worpen maakt, wat is dan de kans dat hij er precies tien maakt?
from scipy.stats import binom #calculate binomial probability binom.pmf(k= 10 , n= 12 , p= 0.6 ) 0.0639
De kans dat Nathan precies 10 vrije worpen maakt is 0,0639 .
Vraag 2: Marty gooit 5 keer een eerlijke munt op. Wat is de kans dat de munt 2 keer of minder kop krijgt?
from scipy.stats import binom #calculate binomial probability binom.cdf(k= 2 , n= 5 , p= 0.5 ) 0.5
De kans dat de munt 2 keer of minder kop oplevert is 0,5 .
Vraag 3: We weten dat 70% van de mensen een bepaalde wet steunt. Als er willekeurig 10 individuen worden geselecteerd, wat is dan de kans dat tussen de 4 en 6 van hen de wet steunen?
from scipy.stats import binom #calculate binomial probability binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 ) 0.3398
De kans dat tussen de 4 en 6 willekeurig geselecteerde individuen de wet ondersteunen is 0,3398 .
Hoe een binominale verdeling te visualiseren
U kunt een binominale verdeling in Python visualiseren met behulp van de seaborn- en matplotlib- bibliotheken:
from numpy import random import matplotlib.pyplot as plt import seaborn as sns x = random.binomial(n= 10 , p= 0.5 , size= 1000 ) sns.distplot(x, hist= True , kde= False ) plt.show()
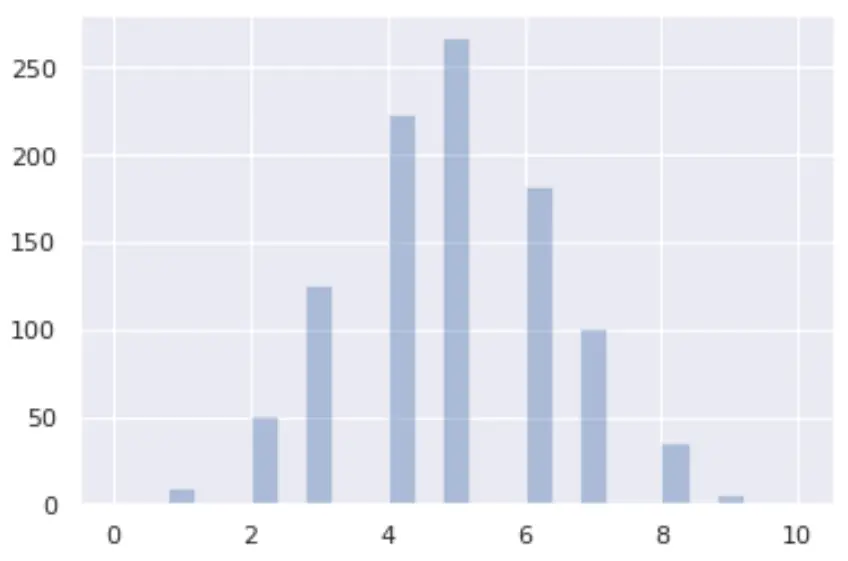
Thee