Binomiale verdeling

Von Dr.benjamin anderson August 3, 2023 Waarschijnlijkheid Keine Kommentare

In dit artikel wordt uitgelegd wat de binominale verdeling in de statistiek is en waarvoor deze wordt gebruikt. U vindt daarom de definitie van de binomiale verdeling, voorbeelden van binomiale verdelingen en de eigenschappen van dit type kansverdeling. Bovendien kunt u elke waarschijnlijkheid van de binomiale verdeling berekenen met een online rekenmachine.

Wat is de binominale verdeling?

De binomiale verdeling is een kansverdeling die het aantal successen telt bij het uitvoeren van een reeks onafhankelijke, dichotome experimenten met een constante kans op succes.

Met andere woorden: de binomiale verdeling is een verdeling die het aantal succesvolle uitkomsten van een reeks Bernoulli-proeven beschrijft.

Bedenk dat een Bernoulli-test een experiment is dat twee mogelijke uitkomsten heeft: ’succes‘ en ‚mislukking‘. Als de kans op ‘succes’ dus p is, is de kans op ‘mislukking’ q=1-p .

Over het algemeen wordt het totale aantal uitgevoerde experimenten gedefinieerd met de parameter n , terwijl p de kans op succes van elk experiment is. Een willekeurige variabele die een binominale verdeling volgt, wordt dus als volgt geschreven:

$X\sim\text{Bin}(n,p)$

Merk op dat in een binominale verdeling exact hetzelfde experiment n keer wordt herhaald en dat de experimenten onafhankelijk van elkaar zijn, dus de kans op succes van elk experiment is hetzelfde (p) .

De binomiale verdeling kan ook binomiale verdeling worden genoemd.

Voorbeelden van binominale verdelingen

Zodra we de definitie van de binomiale verdeling hebben gezien, zullen we verschillende voorbeelden zien van variabelen die dit type verdeling volgen om het concept beter te begrijpen.

Aantal keren dat er kop verschijnt als je 25 keer een munt opgooit.
Aantal schoten dat een basketbalspeler maakt wanneer hij vanaf dezelfde locatie 60 keer richting de basket schiet.
Aantal keren dat we het getal 6 krijgen door 30 keer met een dobbelsteen te gooien.
Aantal geslaagden op een totaal van 50 studenten die een examen afleggen.
Aantal defecte eenheden in een steekproef van 100 producten.

Binomiale verdelingsformule

Gegeven de parameters x, n, p, wordt de waarschijnlijkheidsfunctie van de binomiale verdeling gedefinieerd als het combinatorische getal van n in x keer p ^x keer (1-p) ^nx .

Daarom is de formule voor het berekenen van de waarschijnlijkheid van een binominale verdeling :

👉 U kunt de onderstaande rekenmachine gebruiken om de waarschijnlijkheid te berekenen van een variabele die de binominale verdeling volgt.

Aan de andere kant wordt de cumulatieve waarschijnlijkheid van de binomiale verdeling berekend door de kansen van het aantal succesgevallen in kwestie op te tellen bij alle eerdere kansen. De formule voor het berekenen van een cumulatieve waarschijnlijkheid van een binominale verdeling is dus:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Opgeloste oefening over de binominale verdeling

We gooien 10 keer een munt op, wat is de kans dat we 6 keer kop krijgen?

De variabele in dit probleem volgt een binominale verdeling omdat alle lanceringen onafhankelijk van elkaar zijn en ook dezelfde kans op succes hebben.

Concreet bedraagt de kans op succes 50%, aangezien slechts één van de twee mogelijke resultaten als een succes wordt beschouwd.

$p=\cfrac{1}{2}=0,5$

Daarom is de verdeling voor deze oefening binomiaal met een totaal van 10 experimenten en een waarschijnlijkheid van 0,5.

$X\sim\text{Bin}(10 ; 0,5)$

Om de kans op zes keer kop te bepalen, moeten we dus de binomiale verdelingsformule toepassen.

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

De kans dat je precies zes keer kop krijgt door tien keer een muntje op te gooien, is dus 20,51%.

Kenmerken van de binominale verdeling

De binominale verdeling heeft de volgende kenmerken:

De binomiale verdeling wordt gedefinieerd met twee parameters: n is het totale aantal Bernoulli-experimenten en, aan de andere kant, p is de kans op succes van elk Bernoulli-experiment.

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

Het gemiddelde van een binominale verdeling is gelijk aan het product van het totale aantal experimenten vermenigvuldigd met de kans op succes van elk experiment. Om het gemiddelde van een binominale verdeling te berekenen, moet men daarom n met p vermenigvuldigen.

$E[X]=n\cdot p$

De variantie van een binomiale verdeling is gelijk aan het totale aantal pogingen vermenigvuldigd met de kans op succes en de kans op mislukking.

$Var(X)=n\cdot p\cdot (1-p)$

De formule voor de waarschijnlijkheidsfunctie van de binominale verdeling is als volgt:

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

Op dezelfde manier is de formule voor de cumulatieve verdelingsfunctie van de binominale verdeling:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

De som van twee onafhankelijke binomiale verdelingen met dezelfde waarschijnlijkheid is equivalent aan een binomiale verdeling met dezelfde waarschijnlijkheidswaarde p en n is de som van het totale aantal pogingen van de twee verdelingen.

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

De Bernoulli-verdeling is een speciaal geval van binomiale verdeling waarin n=1 , dwz dat er slechts één experiment wordt uitgevoerd.

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_Als _X 1 , _X ₂ ,…, X _k onafhankelijke willekeurige variabelen zijn zodat

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

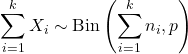
Binomiale verdelingscalculator

Voer de waarden van de parameters p, n en x van de binominale verdeling in de volgende rekenmachine in om de waarschijnlijkheid te berekenen. U moet de waarschijnlijkheid selecteren die u wilt berekenen en de getallen invoeren met de punt als decimaal scheidingsteken, bijvoorbeeld 0,1667.

Über den Autor

Dr.benjamin anderson

Ik ben Benjamin, een gepensioneerde hoogleraar statistiek die nu een toegewijde Statorials-lesgever is. Ik heb uitgebreide ervaring en expertise op het gebied van statistiek en ik ben vastbesloten om mijn kennis te delen met studenten via Statorials. Lees verder