Bivariate analyse uitvoeren in python: met voorbeelden

De term bivariate analyse verwijst naar de analyse van twee variabelen. U kunt dit onthouden omdat het voorvoegsel “bi” “twee” betekent.

Het doel van bivariate analyse is om de relatie tussen twee variabelen te begrijpen

Er zijn drie veelgebruikte manieren om bivariate analyses uit te voeren:

1. Puntenwolken

2. Correlatiecoëfficiënten

3. Eenvoudige lineaire regressie

Het volgende voorbeeld laat zien hoe u elk van deze soorten bivariate analyses in Python kunt uitvoeren met behulp van de volgende panda’s DataFrame die informatie bevat over twee variabelen: (1) Uren besteed aan studeren en (2) Examenscore behaald door 20 verschillende studenten:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df. head ()

	hours score
0 1 75
1 1 66
2 1 68
3 2 74
4 2 78

1. Puntenwolken

We kunnen de volgende syntaxis gebruiken om een spreidingsdiagram te maken van de bestudeerde uren versus de examenresultaten:

 import matplotlib. pyplot as plt

#create scatterplot of hours vs. score
plt. scatter (df. hours , df. score )
plt. title (' Hours Studied vs. Exam Score ')
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

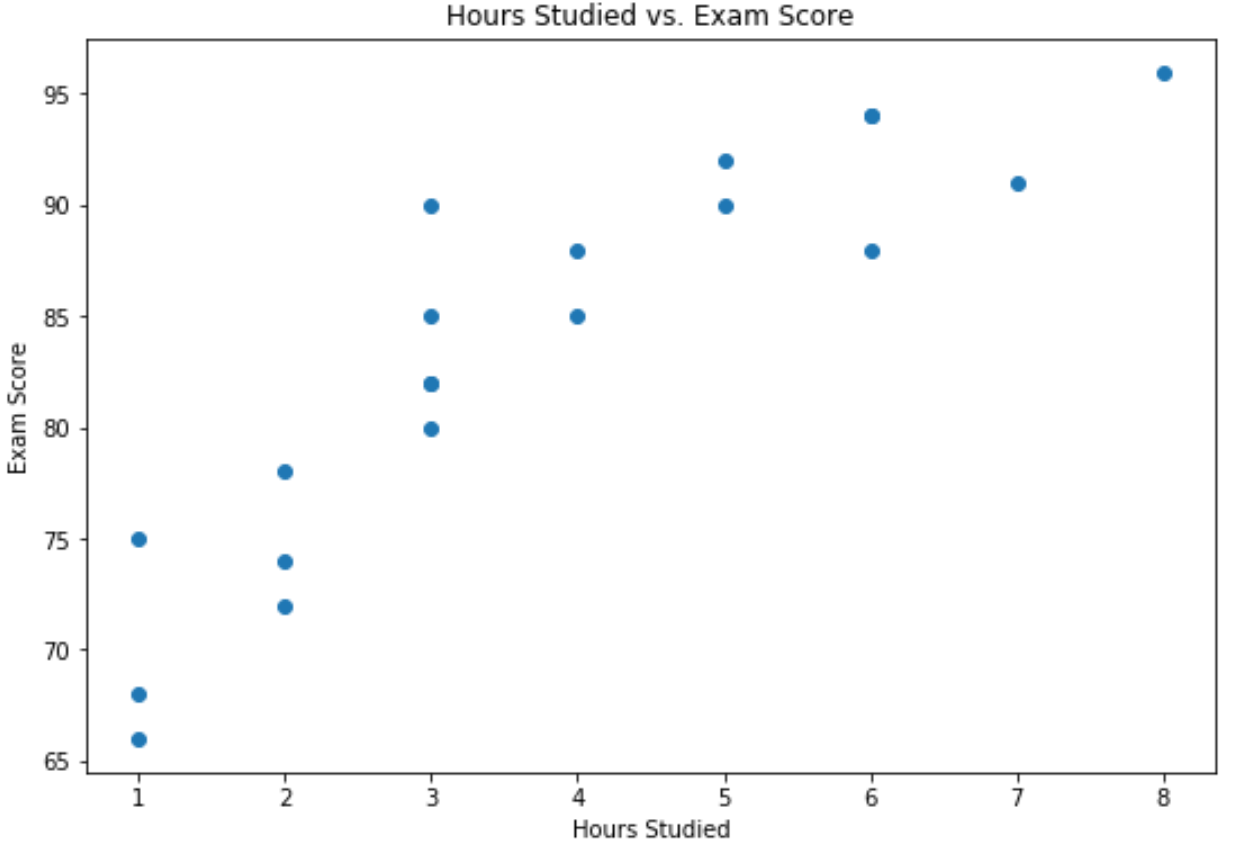
Op de x-as staan de bestudeerde uren en op de y-as het behaalde cijfer voor het examen.

Uit de grafiek blijkt dat er een positief verband bestaat tussen beide variabelen: naarmate het aantal studie-uren toeneemt, stijgen ook de examenscores.

2. Correlatiecoëfficiënten

Een Pearson-correlatiecoëfficiënt is een manier om de lineaire relatie tussen twee variabelen te kwantificeren.

We kunnen de functie corr() in panda’s gebruiken om een correlatiematrix te maken:

 #create correlation matrix
df. corr ()

	hours score
hours 1.000000 0.891306
score 0.891306 1.000000

De correlatiecoëfficiënt blijkt 0,891 te zijn. Dit duidt op een sterke positieve correlatie tussen het aantal gestudeerde uren en het examencijfer.

3. Eenvoudige lineaire regressie

Eenvoudige lineaire regressie is een statistische methode die we kunnen gebruiken om de relatie tussen twee variabelen te kwantificeren.

We kunnen de functie OLS() uit het statsmodels-pakket gebruiken om snel een eenvoudig lineair regressiemodel in te passen voor de bestudeerde uren en ontvangen examenresultaten:

 import statsmodels. api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.794
Model: OLS Adj. R-squared: 0.783
Method: Least Squares F-statistic: 69.56
Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07
Time: 16:15:52 Log-Likelihood: -55,886
No. Observations: 20 AIC: 115.8
Df Residuals: 18 BIC: 117.8
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 69.0734 1.965 35.149 0.000 64.945 73.202
hours 3.8471 0.461 8.340 0.000 2.878 4.816
==================================================== ============================
Omnibus: 0.171 Durbin-Watson: 1.404
Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177
Skew: 0.165 Prob(JB): 0.915
Kurtosis: 2.679 Cond. No. 9.37
==================================================== ============================

De gepaste regressievergelijking blijkt te zijn:

Examenscore = 69.0734 + 3.8471*(uren gestudeerd)

Dit vertelt ons dat elk extra uur dat wordt gestudeerd, gepaard gaat met een gemiddelde stijging van 3,8471 in de examenscore.

We kunnen de gepaste regressievergelijking ook gebruiken om de score te voorspellen die een student zal behalen op basis van het totale aantal bestudeerde uren.

Een student die bijvoorbeeld 3 uur studeert, zou een score van 81,6147 moeten behalen:

• Examenscore = 69.0734 + 3.8471*(uren gestudeerd)
• Examenscore = 69,0734 + 3,8471*(3)
• Examenresultaat = 81,6147

Aanvullende bronnen

De volgende tutorials bieden aanvullende informatie over bivariate analyse:

Een inleiding tot bivariate analyse
5 voorbeelden van bivariate gegevens in het echte leven
Een inleiding tot eenvoudige lineaire regressie
Een inleiding tot de Pearson-correlatiecoëfficiënt